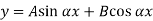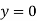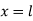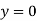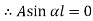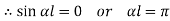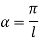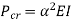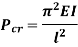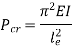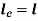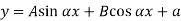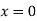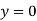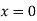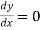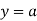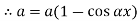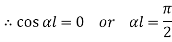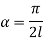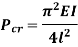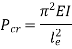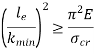undefined | unit 4 buckling of long columns

Back to Study material

Unit - 4Buckling of Long ColumnsQ1) A 4 m long hollow alloy tube with inside and outside diameter are 36 mm and 48 mm elongates by 3 mm under a tensile force of 50 kN. Determine the buckling load for the tube when it is used as a column with both ends pinned and with factor of safety 5.A1)

Q2) Determine the shortest length for a pin-joined steel column of cross-section 75 mm x 48 mm using Euler’s Formula. Take critical stress value as 220 MPa and E = 205 MPa.A2)

Q3) A 4 m log circular bar deflects 20 mm at the center when used as simply supported beam under a 200 N load at center. Determine critical load for the same bar when used as a strut which is firmly fixed at one end and pin joined at other.A3)

Q4) Using Euler’s Formula, determine the critical stresses for the strut of slenderness ratio 80,120, 160 and 200 under a condition of (a) both ends hinged and (b) both ends fixed. Take E = 205 GPa.A4)

Q5) Give the assumptions made in Euler’s theory.A5) Assumptions made in Euler’s Theory

The column should be axially loaded

The column material is perfectly elastic, homogeneous and isotropic and hence obeys Hooke’s law.

The column should be perfectly straight and uniform in cross-section throughout its length

Length of column is very large as compared its cross-sectionl dimensions.

Direct stress are negligible compared to bending stress.

Plane cross-section remains plane and normal to the center line during the buckling.

Self weight of the column is neglected.

Q6) Derive the effective length of column with both ends hinged

A6)

Y-axis is taken in such a way that deflection is positive.

From the equation of bending, viewing from right end,

The equation can be written as

Where,

The solution of the above equation is

When both ends are hinged.

At ,

And at ,

If A = 0, y is zero for all values of load, hence, there is no bending.

Therefore, Euler’s Crippling load,

Comparing above equation with

We get,

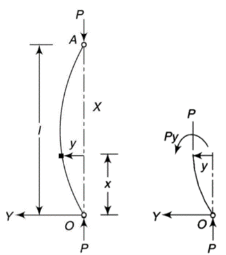
Q7) Derive the effective length of column with one end fixed and other free.

A7)

Take Y-axis towards right for positive value of y. Viewing from left we get,

The equation can be written as

Where,

The solution of the above equation is

When one end is fixed and other is free.

At ,

Therefore, Euler’s Crippling load,

Comparing above equation with

We get,

Q8) Explain the limitation of Euler’s theory.A8)

Crippling stress is given by,

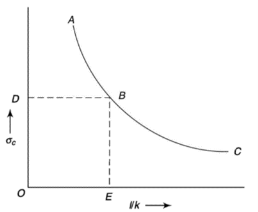
The critical stress is directly proportional to modulus of elasticity and inversely proportional to square of slenderness ratio of column.

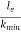The graph plotted between critical stress and slenderness ratio is shown in figure below.

The value of

at point B is called as critical value of slenderness ratio.For any slenderness ratio above this value, column fails for buckling and for any value of slenderness ratio less than this value, the column fails by crushing and not by buckling.Hence, for short column, Euler’s Formula is not applicable.Mathematically, Euler’s Formula is applicable,If crushing stress

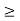buckling stress

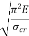When the slenderness ratio is greater than or equal to

, then the Euler’s formula is applicable. This is the limitation of Euler’s formula. Q9) A 1.5 m long column has circular cross-section of 50 mm diameter. One end of column is fixed in direction and position and another end is free. Taking a factor of safety of 3, calculate safe load using Rankine’s formula. Take

and

Q10) Compare the crippling load given by Euler’s and Rankine’s formula for a tabular steel strutb2.3 m long having external diameter = 38 mm, strut is fixed at one end and hinged at another end.

Take and . Take and .

A10)

Sign Up