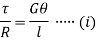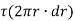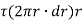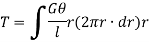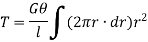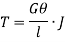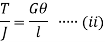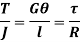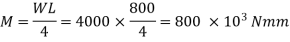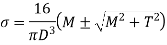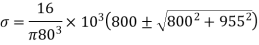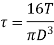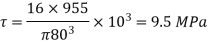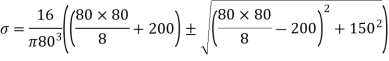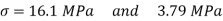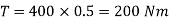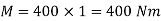SM
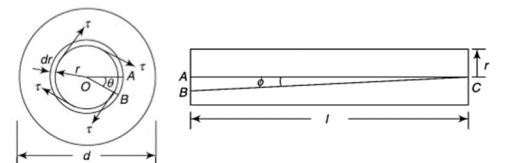
Unit - 6Torison Of Circular ShaftQ1) Derive Torsion equation. And comment on the equation for shear stress distribution.A1) Figure below shows a circular shaft of length l and diameter d acted upon by a torque T.
The shear strain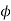 
of elements at radial distance r form the axis is constant for a particular value of T. The line OA thus twists to OB.
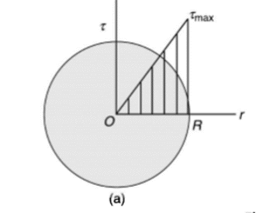
Torsion equation shows that for a given shaft, shear stress is proportional to the radius of shaft. Figure below shows a shear stress distribution in solid shaft of Radius R.
Q2) What are the assumptions in Torsion theory?A2) Assumptions in Torsion TheoryThe bar is acted upon by a pure torque. The section under consideration is remote from the point of application of the load and from a change in diameter. Adjacent cross sections originally plane and parallel remain plane and parallel after twisting, and any radial line remains straight. The material obeys Hooke’s law Cross-sections rotate as if rigid, i.e. every diameter rotates through the same angle Q3) A hollow steel shaft transmits 200 kW of power at 150 rpm. The total angle of twist in a length of 5 m of the shaft is 3o. Find the inner and outer diameters of the shaft if the permissible shear stress is 60 MPa. Take G = 80 GPa.A3)
Q4) Compare the length of equal length of a solid and a hollow shaft to transmit a given torque for the same maximum stress if the inside diameter of shaft is three fourth of the outside.A4)
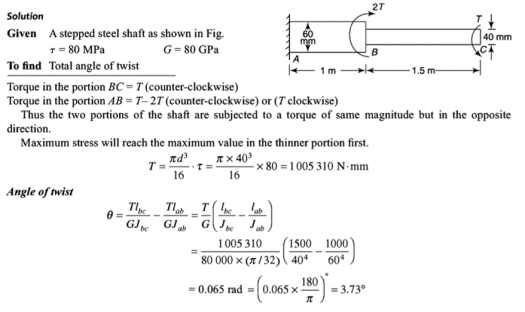
Q5) Figure shows a stepped steel shaft. It is subjected to a torque T at the free end and a torque 2T in the opposite direction at the junction of two sizes. Determine the total angle of twist if the maximum shear stress is limited to 80 MPa. G = 80 GPa.A5)
Q6) Figure shows a hollow shaft. Determine the maximum power transmitted by shaft at 200 rpm if the shear stress in the shaft is not to exceed 70 MPa. Also find the lengths of the two portions if the twist produced in the two portions of the shaft are equal.A6)
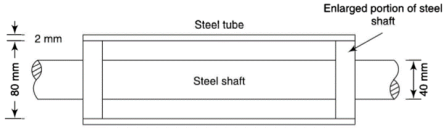
Q7) A circular steel shaft of 40 mm diameter is provided with enlarged portion of 80 mm diameters at two ends as shown in fig. On the enlarged portion a steel tube of 2 mm thickness is shrunk. During the shrunk process, the 40 mm diameter shaft is held twisted by a couple of magnitude of 800 N.m. When the tube is firmly set on the tube, the couple is removed. Determine the twisting couple left on the shaft if the tube and the shaft are made of same material.
A7)
Q8) An 800 mm long shaft with a diameter of 80 mm carries a flywheel weighing 4 kN at its midway. The shaft transmits 24 kW at a speed of 240 rpm. Determine the principal stresses and the maximum shear stress at the end of a vertical and horizontal diameter in a plane near the flywheel.A8)
Q9) The outer and inner diameters of a hollow steel shaft are 120 mm and 60 mm respectively. The shaft transmits 800kW at a speed of 400 rpm while an end thrust of 70 kN acts on the shaft. Determine the bending moment which can safely be applied to the shaft if the maximum principal stress does not exceed 80 MPa.A9)
Q10) Determine the principal stress on the circular shaft with diameter 80 mm subjected to axial thrust of 80 kN, bending moment of 200 Nm and twisting moment of 150 Nm.A10)
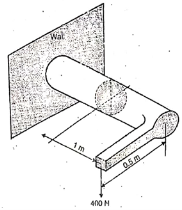
Q11) A 100 mm diameter bar with a built in bracket is fixed to the wall and loaded as shown in figure. Determine the principal stresses at the top extremity of vertical diameter for the section marked A.
A11)
The principal stresses at the top extremity of the vertical diameter, at the section A
|
of elements at radial distance r form the axis is constant for a particular value of T. The line OA thus twists to OB.Let
Now, tangential force on the element = Moment of tangential force on the element = Sum of moments for the whole shaft,
But Thus
From (i) and (ii)
This equation is called as Torsion Equation.
|
|
|
|
|
|
|
|
Given: L = 800 mm D = 80 mm W = 4 kN P = 24 kW N = 240 rpm Sol:
At the end of vertical diameter, Principle stress is
|
Maximum shear stress is given by,
At the ends of horizontal diameter, The bending stress is zero Ans hence, maximum shear stress is
|
|
Given: D = 80 mm P = 80 kN M = 200 kN mm T = 150 kN mm Solution:
|
|
Torsion at section A
Bending Moment at section A
|
|
0 matching results found