undefined | unit 4 curves

SURVEY2

UNIT-4Curves Q1) What is curve and its necessity?A1) When two straight lines intersect at some angle then a curve is provided in between them which meets the straight line tangentially.Curve are in fact Arc with some definite radius and center that is they are a part of circle. it is due to the curves only that the change in direction is made possible a very smooth taskNecessity (Curves are provided for following reasons)

Curves are needed on highways Railways and Canal for bringing about gradual change of direction of motion

to bring about gradual changes in direction of motion

to connect important places

to avoid obstructions

to bring about gradual changes in grade and for good visibility

to balance earthquake in acceleration cutting

minimizing construction cost

Q2) What are the types of curves?A2)

Q3) What are the element in simple curve?A3)

Q4) What are the element in compound curve?A4) Compound curve has seven elements

Radius R1,

Radius R2,

deflection angle φ,

deflection angle of the first arc φ1,

deflection angle of the second arc φ2,

tangent length LT1 and LT2.

Elements of Compound Curves

Common tangent = MN = MD + DN = R1 tan (∆ 1 /2) + R2 tan (∆ 2 /2)

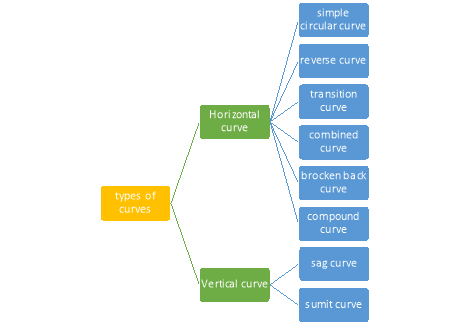
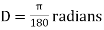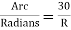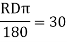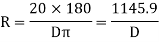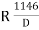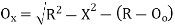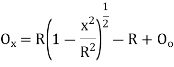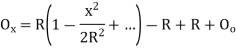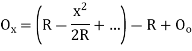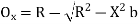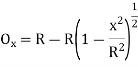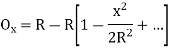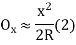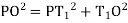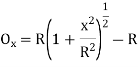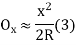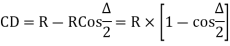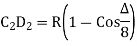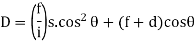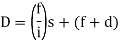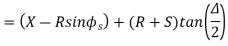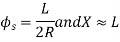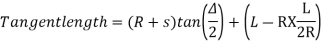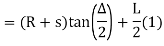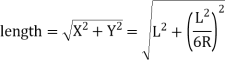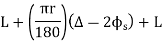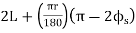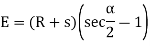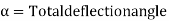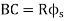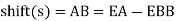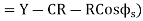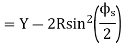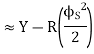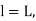∆ = ∆ 1 + ∆ 2

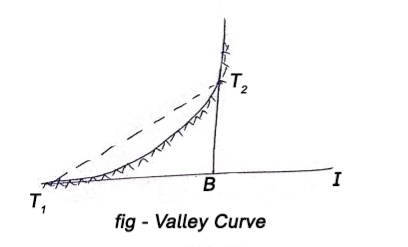
Length of the main tangents IT1 and IT2:

IT1 = T1M + MI = R1 tan ∆ 1 /2 + MN sin ∆ 2 /sin ∆
IT2 = T2N + NI = R2 tan ∆ 2 /2 + MN sin ∆ 1 /sin ∆ 2

Q5) What is the relation between degree and radius of curve?

A5) Arc definition of degree of curve: According to this, degree of curve in the central angle subtended by an arc of length of 20m or 30 m.

If R = radius of curve

D = degree of curve as per arc definition for 30m arc length.

D° =

Q (radians) =

For 20 mm length

(2)

Q6) What is setting out of compound curve?A6) Setting a compound curve

Calculate all elements ∆1 , ∆2, ∆, R1, R2, IT2 and IT1.

Locate PI (I), PC (T1) and PT (T2)

Calculate chainage of T1 (chainage of I – tangent length IT1)

Calculate chainage of the point of compound curvature D.

Chainage of D = Chainage of T1 + length of arc T1D = chainage of T1 + ΠR1 ∆1 / 180oCalculate chainage of T2 = chainage of D + ΠR2 ∆2 / 180o

Calculate the deflection angles for both the arcs from their tangents, e.g. ∆1 = δ1 = 1719 C1 / R, where C1 is the chord length and R is the radius

Q7)What is the setting out of simple curve?A7)

) Method of setting out curve

(a) Linear method

(i) Offset from long chord

Where

offset at some point P at distance x from midpoint D.

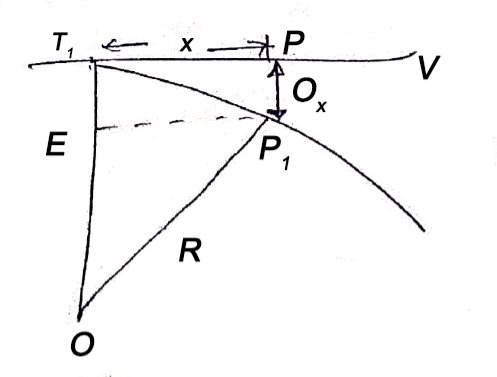
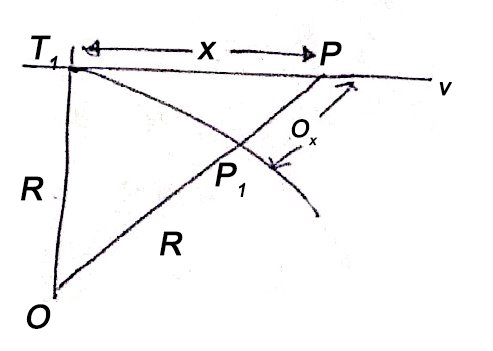
(ii) Perpendicular offset from tangent

$C:\Users\Namrah\Desktop\pic\309.jpg$

(iii) Radial offset from tangent:

$C:\Users\Namrah\Desktop\pic\310.jpg$

(iv) Successive Bisection of Arc or chord

$C:\Users\Namrah\Desktop\pic\311.jpg$

(v) By offset from chord produced

last sub chord

b) Angular method

i) Rankine's method of deflection angle

- It is generally used for setting out a circular curve of long length and large radius.

- It give good result except then chords are long as compared to radius, so that variation between length of an Arc and its cord becomes considerable.

- It is used in highway and Railway

= Tangential angle

C = chord length

(ii) Tachometric method

-It is similar to Rankine’s method of deflection angle.

- The theodolite at may be used as Tacheometric and Tacheometric observation are made.

- Less accurate as compared to Rankins.

- Chaining is completely dispersed in this method.

(For Incline and line of sight)

(For horizontal line of sight)

ii) Two theodolite method

- Convenient than any of to our method when ground is undulating rough and not suitable for Linear measurements.

- Two theodolite are used and linear measurement are completely eliminated.

- Hence, most accurate method.

- It is based on principle that angle between the tangent and chord is equal to angle subtended by chord in opposite segment.

- Time consuming method

- Most accurate method

- Highly expensive.

Q8) Explain types of vertical curves?A8) Types of vertical curvesi) Upgrade followed by a downgrade

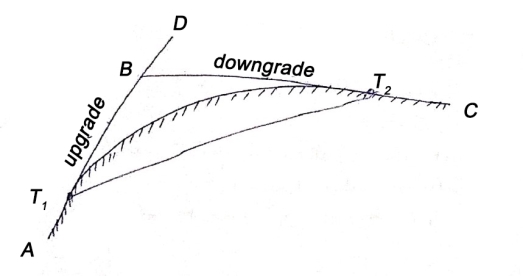
$C:\Users\Namrah\Desktop\pic\305.jpg$

ii) Upgrade followed by another upgrade

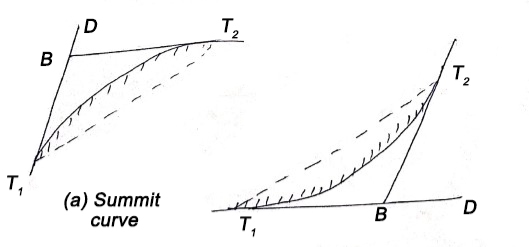
$C:\Users\Namrah\Desktop\pic\306.jpg$

iii) A downgrade followed by an upgrade

$C:\Users\Namrah\Desktop\pic\307.jpg$

iv) A downgrade followed by an another downgrade Q9) Write the element of trasntition curve?A9) (a)Total Tangent Length

$C:\Users\Namrah\Desktop\pic\302.jpg$

Tangent length

(b) Length of long chord

Total length of curve

=Total length (3)

(d) Apex distance E

Q10) What is the design procedure of compound curve?A10) Step 1 : Locate tangent point T, by measuring back the total tangent length (Tt) along back tangent, from the point of intersection V.

Likewise, locate the tangent point T' by measuring along forward tangent the distance Tt from V.

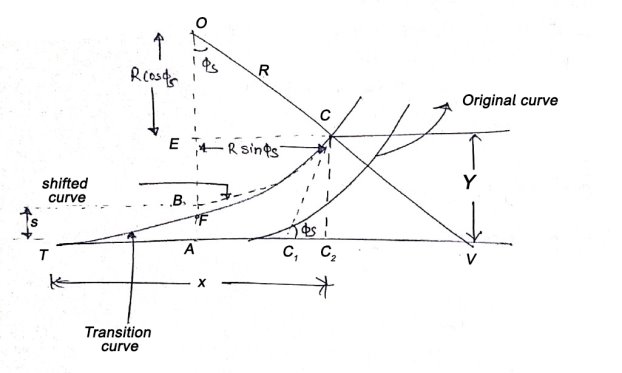
Setting out of transition curve :

Step 2 : Set a theodolite over the point T. Set vernier A to zero, and clamp the upper plate.

Step 3 : Direct the line of sight of theodolite to intersection point V, and clamp lower plate.

Step 4 : Release upper plate. Set the vernier A to first deflection angle (a1).

The line of sight now points towards the first peg on transition curve.

Step 5 : With the zero of the tape pinned at T and an arrow kept at mark corresponding to the first length of the chord, assistant will swing the tape till the arrow is bisected by line of sight.
Fix the first peg at arrow point.

Step 6 : Set the vernier A on the second deflection angle (a2) to direct line of sight to the second peg.

Step 7 : With zero of the tape pinned at T, and keeping an arrow at mark corresponding to the total length of the first and second chords, assistant will swing an arc till the arrow is bisected by the line of sight.

Fix the second peg at arrow point. It should be remembered that the distance is measured from the point T and not from preceeding point.

Step 8 : repeat steps (6) and (7) till the last point C on transition curve is reached.

Setting out of the circular curve :
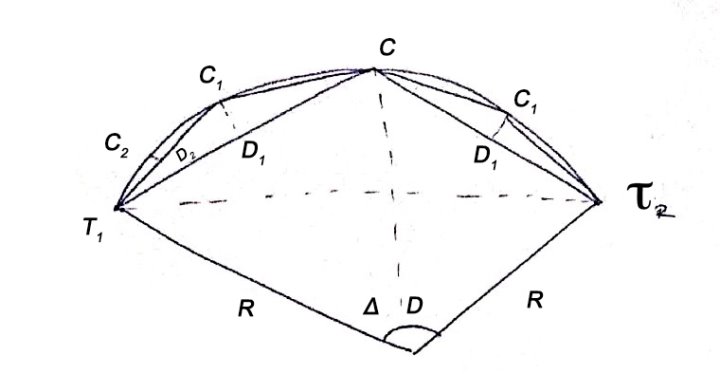
Step 9 : For setting out circular curve CC', shift the theodolite to junction point C.

Orient theodolite with reference to the common tangent CC1 by directing line of sight towards CT with vernier. A set at a reading equal to , and swinging the telescope clockwise in azimuth by fs(Figure 39.4).

Now line of sight is directed along the common tangent CC1 and the vernier reads zero.

Step 10 : Plunge telescope. The line of sight is now directed along the tangent C1C produced.

deflection angles D1, D2, etc. have been calculated with reference to the tangent C1C produced at C (Figure 38.2).

The line of sight is now correctly oriented, and reading of the vernier A is zero.

Step 11 : Set the vernier A to first deflection angle D1, and locate the first peg on circular curve at a distance of c' from C, where c' is length of the first sub-chord.

Step 12 : Likewise, locate the second peg on circular curve at the distance c equal to the normal chord from first peg with the deflection angle D2 at C.

Step 13 : Continue the above process till junction point C' is reached.

Step 14 : Set out the transition curve T'C' from T' using same procedure as that for transition curve TC.

Sign Up