Unit - 1

Matrices and Solution of Linear System Equations

Question and answer

1. Reduce the following matrix into normal form and find its rank,

Let A =

Apply we get

     A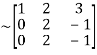 

Apply 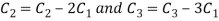we get

        A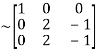 

Apply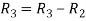

      A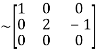 

Apply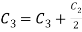

     A 

Apply 

     A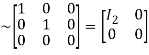 

Hence the rank of matrix A is 2 i.e. .

2.     Reduce the following matrix into normal form and find its rank,

Let A =   

Apply and

               A

Apply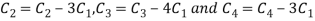

               A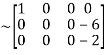

Apply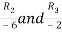

                  A

Apply

                     A

Apply

                      A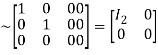

Hence the rank of the matrix A is 2 i.e. .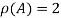

3.     Reduce the following matrix into normal form and find its rank,

Let A =

Apply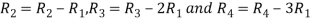

Apply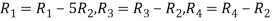

Apply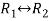

Apply 

Apply 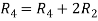and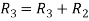

Apply

Hence the rank of matrix A is 2 i.e. .

4.     Solve the equations:

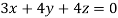
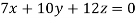
Let the coefficient matrix be A =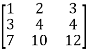  

Apply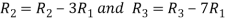

A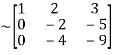

Apply 

         A

Since |A| ,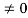 

Also number of equation is m=3 and number of unknowns n=3

Since rank of coefficient matrix A = n number of unknowns

The system of equation   is consistent and has trivial zero solution.

That is  

5.     Solve completely the system of equations

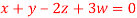
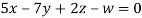
Solution: We can write the given system of equation as AX=0

                     Or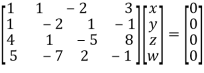

Where coefficient   matrix A  =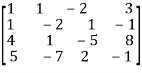

    Apply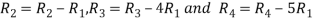 

A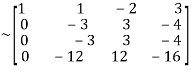  

Apply

          A        …(i)

Since  |A|=0   and  also 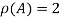, number of  equations m =4  and   number  of unknowns  n=4.

Here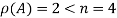 

So that the system has (n-r) linearly independent solution.

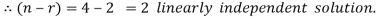
Let

Then from equation (i) we get

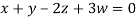
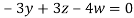
Putting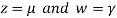 

We get 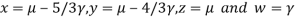  has infinite   number solution.

6.     find the value of λ for which the equations

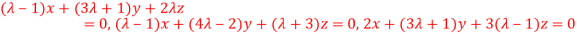
Are consistent, and find the ratio of x: y: z when λ has the smallest of these values. What happen when λ has the greatest o these values?

The system of equation is consistent only if the determinant of coefficient matrix is zero.

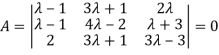
Apply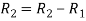

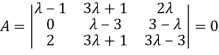
Apply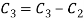 

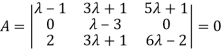
Or 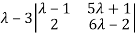=0

Or

Or (

Or (

Or 

Or 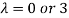………….(i)

1. When λ =0, the  equation become 

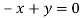
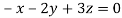
3z=0

On solving we get

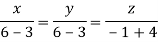
Hence x=y=z

II.                 When λ=3, equation become identical.

7.     Solve the system of equations:

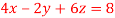
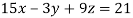
We can write the system as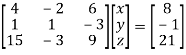

Apply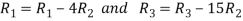

Apply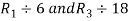

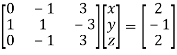
Apply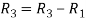 

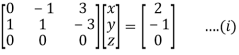
Here coefficient matrix A=  then 

And augmented matrix K=  then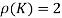 

Since rank of coefficient matrix and   augmented matrix are equal   and is less than the number of unknowns. Therefore system have (n-r) =3-2=1, linearly independent solutions.

From equation (i) we have

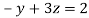
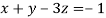
Let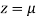 

       So,

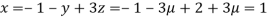
Hence 

Hence system   has infinite   number of solutions.

8.     Investigate for what value of λ and µ the simultaneous equations:

Have (i) no solution

(ii) Unique solution

(iii) An infinite number of solutions.

We can write the given system as

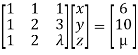
Apply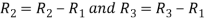

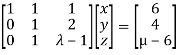
Apply

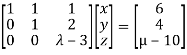
Here the coefficient matrix is A= and augmented matrix K=

1. The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if .

So, λ=3 and µ≠10 in case of no solution.

II.                 In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.

This is possible only if as n=3

This implies that 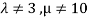  for unique solution.

III.               In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns

This is possible only if as n=3.

This implies that   for infinite solution.

9.     Find the values of a and b for which the equations

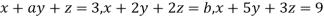
Are consistent. When will these equations have a unique solution?

We can write the above system as

Apply

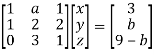
Apply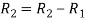

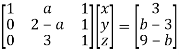
Apply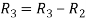

Here the coefficient matrix is A =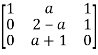

And augmented matrix K is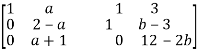

1. The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if .

So, a=-1 and b≠6 in case of no solution

II.                 In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.

This is possible only if

So,   for unique solution.

III.               In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns

This is possible only if 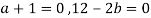as n=3.

This implies that   for infinite solution.