Unit 6

Unit 6

Unit 6

Partial Differentiation

Question and answer

1. Solve:

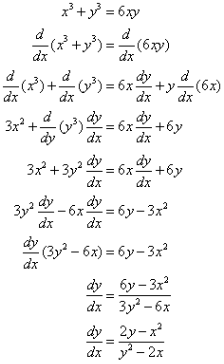
2.    Solve:

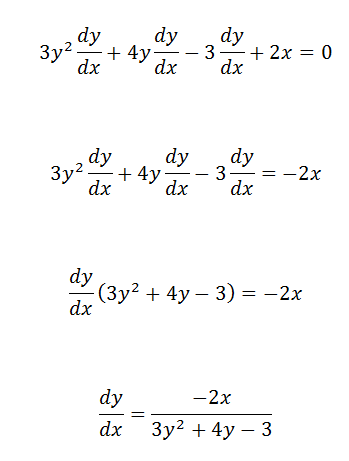
3.    

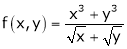
Consider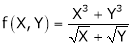

Put

.

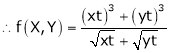
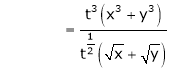
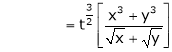
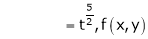Thus degree of f(x, y) is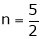

4.     If . f ( x , y ) has a maximum or minimum at point ( a , b ) [ i.e. ( a , b ) is a point of inflection ], then

f x = 0 . . . And . . . f y = 0 , . At ( a , b )

Now put δf ( a , b ) = f ( a + h , b + k ) – f ( a , b )

So at a maximum or minimum

δf .≈ h 2 f x x + k 2 f y y + 2 h k f x y

So f has a maximum at ( a , b ) if . . . f x = 0 . . . And . . . f y = 0 , . . . And . . . δf < 0 for all small h and k . Similarly it has a maximum if . . . δf > 0 for all small h and k . In particular . . . f xx < 0 . . . And . . . f yy < 0 . . . For a maximum ( putting h = 0 and k = 0 respectively) and . . . f xx > 0 . . . And . . . f yy > 0 . . . For a minimum

The approximation for δf can be written:

δf . . . ≈ .( ( h f xx + k f xy ) 2 – k 2 ( f xy 2 – f xx f yy ) ) ⁄ 2 f xx ,providing . . . f xx ≠ 0.

Or . .  δf .≈ ( Θ2 – k 2 Δ ) / 2 f xx , where Θ = ( h f xx + k f xy ) ,

And . . . Δ = ( f xy 2 – f xx f yy ) .

Note that . . . ( Θ2 – k 2 Δ ) . . . Is positive if Δ is zero or negative, and that Δ is not dependant on the values of h and k . So for a point of inflection we have:

• Δ ≤ 0 . . . And . . . f xx > 0 . . . ⇒. . . δf > 0 . . . ⇒. . . Minimum.
• Δ ≤ 0 . . . And . . . f xx < 0 . . . ⇒. . . δf < 0 . . . ⇒. . . Maximum.
• Δ> 0 . . . Then the value of δf is dependant on h and k , so this is a saddle-point.

What if f xx = 0 ? . . . Note that the original approximation for δf is symmetic in x , y , h and k . So we can write

δf . . . ≈ ( Λ2 – h 2 Δ ) / 2 f yy , where Λ = ( k f yy + h f xy ) , Δ same as above.

And note that if f xx = 0 then Δ is positive, so we will have a saddle-point. A completely symmetric argument holds for f yy = 0.

5.     Determine the critical points and locate any relative minima, maxima and saddle points of function f defined by
f(x , y) = 2x2 + 2xy + 2y2 - 6x

Solution
Find the first partial derivatives fx and fy.
fx(x,y) = 4x + 2y - 6
fy(x,y) = 2x + 4y
The critical points satisfy the equations fx(x,y) = 0 and fy(x,y) = 0 simultaneously. Hence.
4x + 2y - 6 = 0
2x + 4y = 0
The above system of equations has one solution at the point (2,-1).
We now need to find the second order partial derivatives fxx(x,y), fyy(x,y) and fxy(x,y).
fxx(x,y) = 4
fyy(x,y) = 4
fxy(x,y) = 2
We now need to find D defined above.
D = fxx(2,-1) fyy(2,-1) - fxy2(2,-1) = ( 4 )( 4 ) - 22 = 12
Since D is positive and fxx(2,-1) is also positive, according to the above theorem function f has a local minimum at (2,-1).
The 3-Dimensional graph of function f given above shows that f has a local minimum at the point (2,-1,f(2,-1)) = (2,-1,-6).