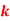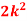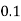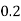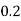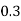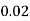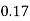Unit-2

PROBABILITY DISTRIBUTION

Q1) Let X be a random variable with PDF given by

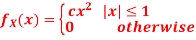
a. Find the constant c

b. Find EX and Var(X)

c. Find P(X)

A1)

 a. To find c, we can use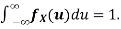

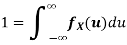
Thus, we must have c=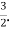

b. To find EX, we can write

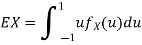
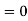
In fact, we could have guessed Ex=0 because the PDF is symmetric around x=0. To find Var(X), We have

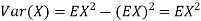
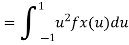
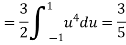
c. To find P(X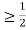), we can write

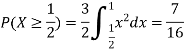
Q2) Let X be a continuous random variable with PDF given by

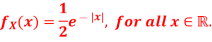
If Y =

A2)

First, we note that

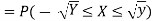
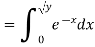
Thus,

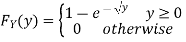
Q3) Let X be a continuous random variable with PDF

Find P(X).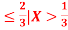

A3)

 We have

P(X) =

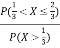
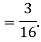
Q4) Consider tossing a fair coin 3 times.

Define X= the number of heads obtained.

A: what is the probability of tossing at least two heads?

B: what is the probability of tossing fewer than three heads?

A4)

X = 0, TTT

X = 1, HTT THT TTH

X = 2, HHT HTH THH

X = 3, HHH

A:  Ans:

B: Ans: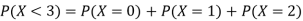

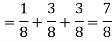
(Or)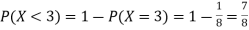

Q 5) Let the random variable X have probability density function

Find the cumulative distribution function of Y = g(x) =

A5)

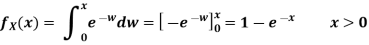
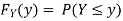
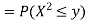
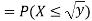
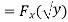
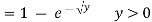
Q 6) There are very few continuous distributions that we can do much with without a lot of math, but the simple uniform distribution is one of them. A uniform distribution is one that is just that-uniform. If we image any possible number between o and 2 as equally likely, we have an infinite possible number of numbers, so the probability of any particular number is close to zero. Instead of focusing on particular numbers, we have to focus on intervals.

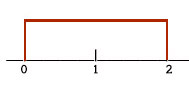
The probability that some number between zero and two will come up will be one. To find the probability of any interval, we find the length of the interval and multiply by 5. Hence, the probability of getting a number between zero and one is 5.

For the following, draw the picture and compute the probabilities. What is:

a):  P(0<x<.8)

b): P(x>.8)

c): P(.5<x<1.5)

d): P(.5<x<1.2) or P(.8<x<1.3)

e): compute the probability that we will not be in the interval of .4 to 1.5

f): compute the middle interval in which we will be 90% of the time.

g): compute the tails (outside intervals) that we will be in 5% of the time

A6)

a):    .8*.5 = .40

b):    1-.4 = .6

c):     1*.5 = .5

d):    P(.5<x<1.5) = .8*.5 = .4

e):    1-P(.4<x<1.5) = 1-1.1*5 = 1-.55 = .45

f):     90% of 2 is 1.8, which centered will be from .1 to 1.9

g):    95% of the time we will be in the interval .05 to 1.95. 5% of the time we will                      

between 0 and .05 or 1.95 and 2.

Q7) Following probability distribution

Find:

(i)    k

(ii)

(iii)                       Distribution function

(iv)                        If 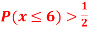  find minimum value of C

(v)  Find

A7)

If P(x) is p.m.f –

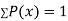
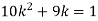
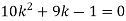
(i)

(ii)

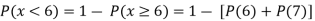
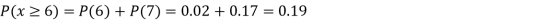
(iii)

(iv)

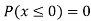
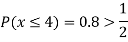
(v)

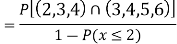
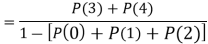
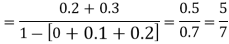
Q 8: The picture below shows a continuous probability distribution with the formula, y = .5x for the range, x =0 to x = 2. In this case, area is probability.

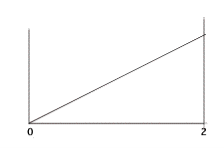
To compute the probability of being between 0 and 1, for example, you need to know y when x equals 1. The formula says it is .5. Hence, to find the probability that x is between 0 and 1 Prob(0<x<1), we compute the area of the triangle with a length of 1 and a height of .5. The answer is 2.5 because .5HW = .5*.5*1.

a).  Show that the area under the line is equal to 1.

b).  Find the following probabilities:

Prob(0<x<.5)

Prob(0<x<1.5)

Prob(1.5<x<2)

Prob(.5<x<1.5)

Prob (x<.5 or x>1.5)

c).  Suppose that we draw twice from this distribution and that probability of the second draw is independent of the first. What is the probability of getting greater than 1.5 on both draws? What is the probability of getting less than 1.5 on both draws? What is the probability of getting a result greater than 1.5 on one draw and less than 1.5 on the other draw?

A8)

a):  Length *height*.5 is the area of a triangle. This triangle has length of 2 and height of 1, so 2*1*.5= 1. The area is one, and for a continuous distribution, area is probability.

b):  Prob(0<x<.5)

Prob(0<x<.5) = .5*.5*.25 = .0625

Prob(0<x<1.5) = .5*1.5*.75 = .5625

Prob(1.5<x<2) = 1-Prob(0<x<1.5) = 1-.5625 = .4375.

Prob(.5<x<1.5) = .5625 - .0625 = .5

Prob (x<.5 or x>1.5) = .0625+.4375 = .5

c):  Both less than 1.5: .5625*.5625 = .3164: both greater than 1.5: .4375*.4375 = .1914; one greater and one less: 1 - .3164 - .1914 = .4922.

Q9) The probability distribution of a discrete random variable X is shown below.

Find:   a) Pr(X)       b) Pr(X<5)      c)   Pr(X>0)      d)    Pr (2)  

e)  Pr(X)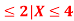 

A9)

a):   Pr(X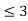) = Pr (X=0)+Pr(X=1)+Pr(X=2)+Pr(X=3)

      = 0.02+0.13+0.38+0.17

     = 0.7.

Working with Discrete Probability Distribution:

Q10)

a): Verify that this is a legitimate probability distribution.

b): What is the probability that a customer does not rent any videos?

A10)

a): Confirm that the sum of the probability is 1.

        0.1+0.4+0.35+0.1+0.05 = 1

b):  This is P(X=0)=0.1 or 10% of customer do not rent any videos.

        Please notice the notation.

Q11) Jean usually makes half of her free throws in basketball practice. Today, she tries 3 free throws. What is the probability that Jean will make exactly 1 of her free throws?

A11)

The Probability that Jean will make each free throw is 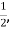or 0.5.

P(r) = Substitute 3 for n, 1 for r, 0.5 for p, and 0.5 for q

P (1) =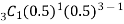

          =   3(0.5)(0.25) = 0.375

The probability that Jean will make exactly one free throw is 37.5%.

Q12) Suppose the probability of purchasing a defective computer is 0.02. What is the probability of purchasing 2 defective computers in a group of 10?

A12)

X = 2, n = 10, and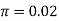

P(X=2) =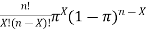

              =

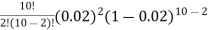
              = (45)(0.0004)(0.8508)

              = 0.01531

Q13) A dozen eggs contain 3 defectives. If a sample of 5 is taken with replacement, find the probability that.

a)     Exactly 2 of the eggs sampled are defective.

b)    2 or fewer of the eggs sampled are defective

A13) If n = 5, P = ¼

“Success = Defective”

x = 0,1,2,3,4,5

f(x) =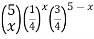

P(X=2) = f (2) =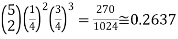

P (X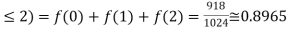

Q14) Suppose that a rare disease has an incidence of 1 in 1000 person-years. Assuming that members of the population are affected independently, find the probability of k cases in a population of 10,000(followed over 1 year) for k=0,1,2.

A14) The expected value (mean)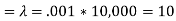

10 new cases expected in this population per year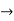

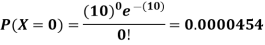
Q 15: Suppose that the probability of a defect in a foot of magnetic tape is 0.002. Use the Poisson distribution to compute the probability that 1500 feet roll will have no defects.

A15)

Q16) The weekly incomes of shit foremen in the glass industry follow the normal probability distribution with a mean of $1,000 and a standard deviation of $ 100. What is the z value for the income, let’s call it X, of a foreman who earns $1,100 per week? For a foreman who earns $900 per week?

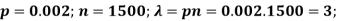
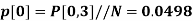
A16)

 For X = $ 1,100:

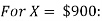
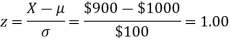
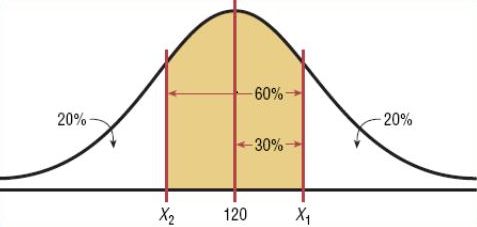
Q17) From the Below Diagram find the area of the both sides of the distribution.

A17)

Area to the left of the positive z: 0.05000+0.3000=0.8000.

Using Table E, z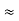0.84. X = 120+0.84(8) =126.72

Area to the left of the negative z= 0.5000-0.3000=0.2000

Using Table E, z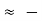0.84. X = 120-0.84(8) =113.28

The middle 60% of readings are between 113 and 127.