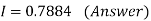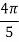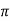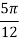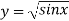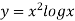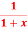Unit – 3
Numerical Integration
Q1) Use Simpson’s Rule to approximate the integral of
f(x) = 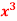 on the interval [1,2].
on the interval [1,2].
A1)
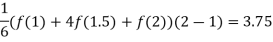
The actual value of the integral is 3.75. This is exact because the error for Simson’s rule is O(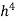 ) and we are integrating a cubic function.
) and we are integrating a cubic function.
Q2) Use Simpson’s Rule to approximate the integral of
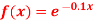 on the interval [2,5].
on the interval [2,5].
A2)
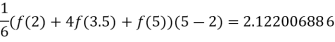
The actual value of the integral is 2.122000934.
Q3) Suppose we can only evaluate a function at the integers (for example, when we are periodically sampling a signal). Use three applications of Simpson’s rule and two applications of Simpson’s 3/8 Rule to approximate the integral of response with a decaying transient f(x) = cos(x)+x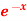 on the interval [0,6].
on the interval [0,6].
A3)
Thus, we calculate:
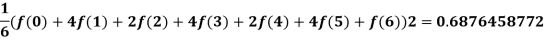
and,

The actual integral is -7exp (-6) + sin (6) +1 = 0.7032332366, and therefore, three applications of Simpson’s rule with intervals of width 2 appears to be more accurate than two applications of Simpson’s 3/8th rule with intervals of width 3.
Q 4: Estimation error of Newton Cotes formula of degree 4.
A4)
From Note (1) we get,

Again, that doesn’t mean that the error is zero. The error term can be obtained from the next term in the Newton Polynomial. i.e.

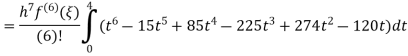
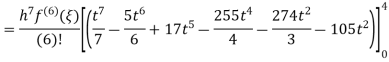

Q 5: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

Estimate the area bounded by the curve, the x axis and the extreme ordinates.
A5)
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =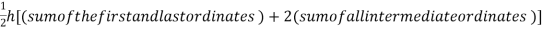
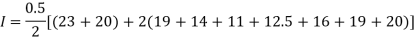
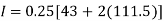
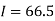
Q6) Compute the value of 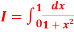 ?
?
A6)
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 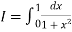
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule


For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
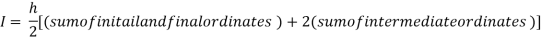
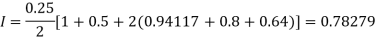
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
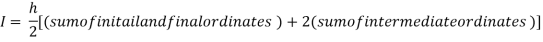
 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
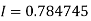
Q7) Evaluate, using trapezoidal rule with five ordinates
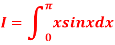
A7)
Here 
We construct the data table:
X | 0 |
|
|
|
|
|
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
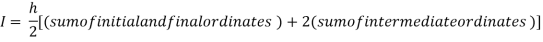
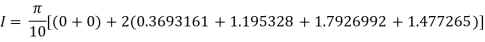
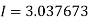
Q8) Estimate the value of the integral
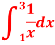
A8)
By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 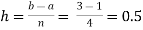
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule

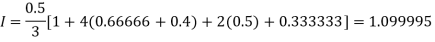
For n = 8, we have 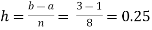
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule


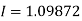
Q 9: Evaluate 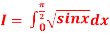
A9)
Using Simpson’s 1/3 rule with 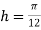 .
.
For 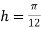 , we construct the data table:
, we construct the data table:
X | 0 |
|
|
|
|
|
|
| 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
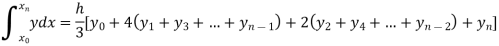
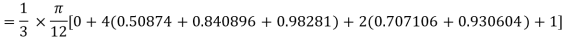
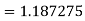
Q10) Using Simpson’s 1/3 rule with h = 1, evaluate 
A10)
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
| 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule

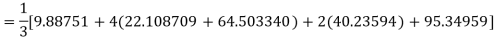
= 177.3853
Q11) Evaluate 
By Simpson’s 3/8 rule.
A11)
Let us divide the range of the interval [4, 5.2] into six equal parts.
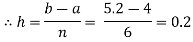
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule


= 1.8278475
Q 12: Evaluate 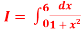
A12)
Let us divide the range of the interval [0,6] into six equal parts.
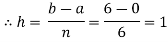
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
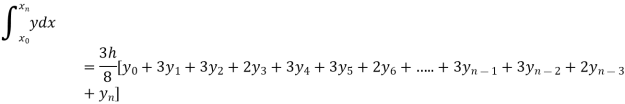
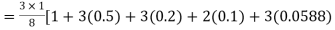 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Q13) Evaluate:

A13)
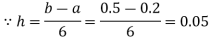
Calculate the values of f(x) = 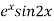
x | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
f(x) | 0.475 | 0.165 | 0.716 | 0.914 | 1.070 | 1.228 | 1.387 |

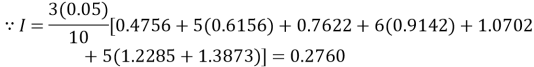
Q14)
x | 0.25 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | 1.75 |
Y= | 0.8 | 0.6666 | 0.5714 | 0.5 | 0.4444 | 0.4 | 0.3636 |
A14)
Weddle’s Rule: It’s a 7-point quadrature formula, i.e. n=6