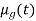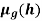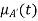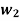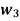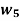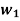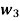Unit – 4
Introduction to Fuzzy sets
Q1) Crisp logic (crisp) is the same as Boolean logic (either 0 or 1). Either a statement is true (1) or it is not (0), meanwhile fuzzy logic captures the degree to which something is true.
A1)
Consider the statement: “The agreed to met at 12’o clock but ben was not punctual.”
Q2) Crisp sets versus Fuzzy sets
A2)
Crisp set Short average under 170cm tall 170 to 180cm over 180cm |
Characteristic Function
Short ave tall
B | A | C |
| short | ave | tall |
A | 0 | 1 | 0 |
B | 1 | 0 | 0 |
C | 0 | 0 | 1 |
Q3)
A3)
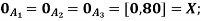
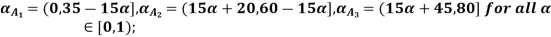
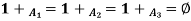
Q4) A fuzzy set A on R is convex iff A(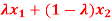 )
)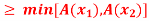
For all 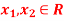 and all
and all  where min denotes the minimum operator.
where min denotes the minimum operator.
A4)
(i) Assume that A is convex and let  Then
Then 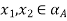 and, moreover,
and, moreover, 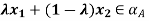 for any
for any 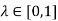 by the convexity o A. Consequently,
by the convexity o A. Consequently,
A (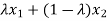 )
)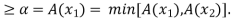
(ii) Assume that a satisfies. We need to prove that for any  is convex. Now for any
is convex. Now for any 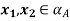 (i.e., A (
(i.e., A ( )
)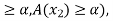 and for any
and for any 
A ( )
)
i.e. 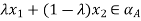 .Therefore,
.Therefore,  is convex for any
is convex for any 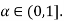 Hence, A is convex.
Hence, A is convex.
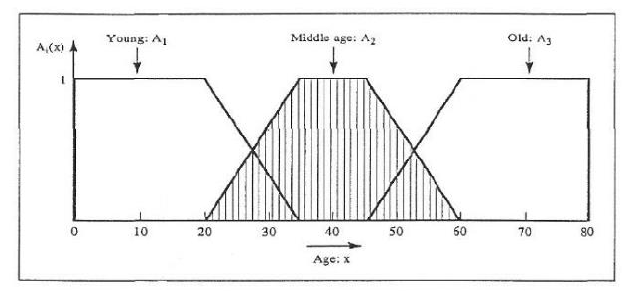
Q5) Consider three fuzzy sets that represent the concepts of a young middle-aged, and old person. The membership functions are defined on the interval [0,80] as follows:
A5)

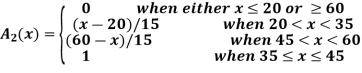

Q6)
t | 20 | 30 | 40 |
| 0.1 | 0.5 | 0.9 |
h | 20 | 50 | 70 | 90 |
| 0.2 | 0.6 | 0.7 | 1 |
| 20 | 50 | 70 | 90 |
20 | 0.1 | 0.1 | 0.1 | 0.1 |
30 | 0.2 | 0.5 | 0.5 | 0.5 |
40 | 0.2 | 0.6 | 0.7 | 0.9 |
Calculated R (t,h) through min operator
A6)
Now suppose, we want to get information about the humidity when there is the following premise about the temperature:
Temperature is fairly high.
This fact is rewritten as R(t): t is 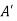 where
where 
Where the fuzzy term  is defined as below membership function of
is defined as below membership function of  in T (temperature)
in T (temperature)
t | 20 | 30 | 40 |
| 0.01 | 0.25 | 0.81 |
R(h)= R(t) o R(t,h)
| 20 | 50 | 70 | 90 |
20 | 0.1 | 0.1 | 0.1 | 0.1 |
30 | 0.2 | 0.5 | 0.5 | 0.5 |
40 | 0.2 | 0.6 | 0.7 | 0.9 |
h | 20 | 50 | 70 | 90 |
| 0.2 | 0.6 | 0.7 | 0.81 |
t | 20 | 30 | 40 |
| 0.01 | 0.25 | 0.81 |
Q 7: Let P = {paris, berlin, Amsterdam} and Q = {Rome, Madrid, Lisbon} be two set of cities, and E = {far, very far, near, very near}. Let R be the fuzzy soft relation over the sets P and Q given by (R,E) = {R(for) = {(paris, Rome)/0.60, (paris, madrid/ 0.45, (Paris, Lisbon)/0.40, (Berlin, Rome)/ 0.50, (Berlin, Madrid)/0.65), (Berlin, Lisbon)/0.70,(Amsterdam, Rome)/0.75, (Amsterdam, Madrid)/0.50,(Amsterdam, Lisbon)/0.80}}.This information can be represented in the form of two-dimensional array(matrix) as shown in the Table 4. It is obvious from the matrix given in table 4 that a fuzzy soft relation may be considered as a parameterized fuzzy relation.
A7)
(1) Union: 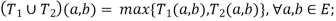
(2) Intersection: 
(3) Containment: 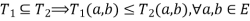
R(far) | Rome | Madrid | Lisbon |
Paris | 0.60 | 0.45 | 0.40 |
Berlin | 0.55 | 0.65 | 0.70 |
Amsterdam | 0.75 | 0.50 | 0.80 |
Q8) Let U = {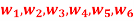 } be the set of watches and A = {cheap, costly}, B = {Beautiful, in a golden locket}. Let (F, A) and (G,B) be two soft sets given by F (cheap) = {
} be the set of watches and A = {cheap, costly}, B = {Beautiful, in a golden locket}. Let (F, A) and (G,B) be two soft sets given by F (cheap) = { .The relation
.The relation 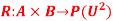 is given by the following membership matrices in table 5 and 6. The membership function of R can also be defined using other appropriate techniques.
is given by the following membership matrices in table 5 and 6. The membership function of R can also be defined using other appropriate techniques.
A8)
R(Costly beautiful) |
|
|
|
|
|
|
| 0.65 | 1 | 0.80 | 0.70 | 0.80 | 0.75 |
| 0.49 | 0.75 | 0.60 | 0.53 | 0.60 | 0.56 |
| 0.52 | 0.80 | 0.64 | 0.56 | 0.64 | 0.60 |
| 0.35 | 0.55 | 0.44 | 0.39 | 0.55 | 0.42 |
| 0.59 | 0.90 | 0.72 | 0.63 | 0.72 | 0.68 |
| 0.53 | 0.85 | 0.68 | 0.60 | 0.68 | 0.64 |