undefined | unit 3 stacks and queues

UNIT- 3

Stacks and Queues

Q1) Explain Pop Operation in stack?

A1)

Accessing the content while removing it from the stack, is known as a Pop Operation. In an array implementation of pop() operation, the data element is not actually removed, instead top is decremented to a lower position in the stack to point to the next value. But in linked-list implementation, pop() actually removes data element and deallocates memory space.

A Pop operation may involve the following steps −

Step 1− Checks if the stack is empty.

Step 2− If the stack is empty, produces an error and exit.

Step 3− If the stack is not empty, accesses the data element at which top is pointing.

Step 4− Decreases the value of top by 1.

Step 5− Returns success.

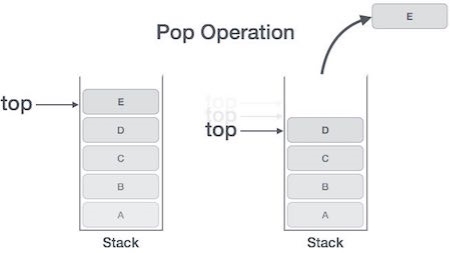
Stack Pop Operation

Algorithm for Pop Operation

A simple algorithm for Pop operation can be derived as follows −

begin procedure pop: stack

if stack is empty

return null

endif

data ← stack[top]

top ← top - 1

return data

end procedure

Implementation of this algorithm in C, is as follows −

Example

int pop(int data) {

if(!isempty()) {

data = stack[top];

top = top - 1;

return data;

} else {

printf("Could not retrieve data, Stack is empty.\n");

}

Q2) Explain Push Operation in stack?

A2)

The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −

Step 1− Checks if the stack is full.

Step 2− If the stack is full, produces an error and exit.

Step 3− If the stack is not full, increments top to point next empty space.

Step 4− Adds data element to the stack location, where top is pointing.

Step 5− Returns success.

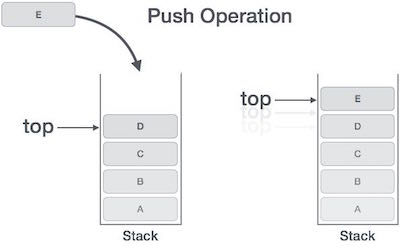
Stack Push Operation

If the linked list is used to implement the stack, then in step 3, we need to allocate space dynamically.

Algorithm for PUSH Operation

A simple algorithm for Push operation can be derived as follows −

begin procedure push: stack, data

if stack is full

return null

endif

top ← top + 1

stack[top] ← data

end procedure

Implementation of this algorithm in C, is very easy. See the following code −

Example

void push(int data) {

if(!isFull()) {

top = top + 1;

stack[top] = data;

} else {

printf("Could not insert data, Stack is full.\n");

}

Q3) What are the Basic Operations in stack?

A3)

Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations −

push()− Pushing (storing) an element on the stack.

pop()− Removing (accessing) an element from the stack.

When data is PUSHed onto stack.

To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks −

peek()− get the top data element of the stack, without removing it.

isFull()− check if stack is full.

isEmpty()− check if stack is empty.

At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it.

First we should learn about procedures to support stack functions −

peek()

Algorithm of peek() function −

begin procedure peek

return stack[top]

end procedure

Implementation of peek() function in C programming language −

Example

int peek() {

return stack[top];

}

isfull()

Algorithm of isfull() function −

begin procedure isfull

if top equals to MAXSIZE

return true

else

return false

endif

end procedure

Implementation of isfull() function in C programming language −

Example

bool isfull() {

if(top == MAXSIZE)

return true;

else

return false;

}

isempty()

Algorithm of isempty() function −

begin procedure isempty

if top less than 1

return true

else

return false

endif

end procedure

Implementation of isempty() function in C programming language is slightly different. We initialize top at -1, as the index in array starts from 0. So we check if the top is below zero or -1 to determine if the stack is empty. Here's the code −

Example

bool isempty() {

if(top == -1)

return true;

else

return false;

}

Q4) Explain Adding a node to the stack (Push operation)?

A4)

Adding a node to the stack is referred to as push operation. Pushing an element to a stack in linked list implementation is different from that of an array implementation. In order to push an element onto the stack, the following steps are involved.

Create a node first and allocate memory to it.

If the list is empty then the item is to be pushed as the start node of the list. This includes assigning value to the data part of the node and assign null to the address part of the node.

If there are some nodes in the list already, then we have to add the new element in the beginning of the list (to not violate the property of the stack). For this purpose, assign the address of the starting element to the address field of the new node and make the new node, the starting node of the list.

Time Complexity : o(1)

DS Linked list implementation stack

C implementation :

void push ()

{

int val;

struct node *ptr =(struct node*)malloc(sizeof(struct node));

if(ptr == NULL)

{

printf("not able to push the element");

}

else

{

printf("Enter the value");

scanf("%d",&val);

if(head==NULL)

{

ptr->val = val;

ptr -> next = NULL;

head=ptr;

}

else

{

ptr->val = val;

ptr->next = head;

head=ptr;

}

printf("Item pushed");

}

Q5) Explain Deleting a node from the stack (POP operation)?

A5)

Deleting a node from the top of stack is referred to as pop operation. Deleting a node from the linked list implementation of stack is different from that in the array implementation. In order to pop an element from the stack, we need to follow the following steps :

Check for the underflow condition: The underflow condition occurs when we try to pop from an already empty stack. The stack will be empty if the head pointer of the list points to null.

Adjust the head pointer accordingly: In stack, the elements are popped only from one end, therefore, the value stored in the head pointer must be deleted and the node must be freed. The next node of the head node now becomes the head node.

Time Complexity : o(n)

C implementation

void pop()

{

int item;

struct node *ptr;

if (head == NULL)

{

printf("Underflow");

}

else

{

item = head->val;

ptr = head;

head = head->next;

free(ptr);

printf("Item popped");

}

Q6) Explain Display the nodes (Traversing)?

A6)

Displaying all the nodes of a stack needs traversing all the nodes of the linked list organized in the form of stack. For this purpose, we need to follow the following steps.

Copy the head pointer into a temporary pointer.

Move the temporary pointer through all the nodes of the list and print the value field attached to every node.

Time Complexity : o(n)

C Implementation

3. void display()

4. {

5. int i;

6. struct node *ptr;

7. ptr=head;

8. if(ptr == NULL)

9. {

10. printf("Stack is empty\n");

11. }

12. else

13. {

14. printf("Printing Stack elements \n");

15. while(ptr!=NULL)

16. {

17. printf("%d\n",ptr->val);

18. ptr = ptr->next;

19. }

20. }

21. }

2. Menu Driven program in C implementing all the stack operations using linked list:

#include <stdio.h>

#include <stdlib.h>

void push();

void pop();

void display();

struct node

{

int val;

struct node *next;

};

struct node *head;

void main ()

{

int choice=0;

printf("\n*********Stack operations using linked list*********\n");

printf("\n----------------------------------------------\n");

while(choice != 4)

{

printf("\n\nChose one from the below options...\n");

printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");

printf("\n Enter your choice \n");

scanf("%d",&choice);

switch(choice)

{

case 1:

{

push();

break;

}

case 2:

{

pop();

break;

}

case 3:

{

display();

break;

}

case 4:

{

printf("Exiting....");

break;

}

default:

{

printf("Please Enter valid choice ");

}

};

}

void push ()

{

int val;

struct node *ptr = (struct node*)malloc(sizeof(struct node));

if(ptr == NULL)

{

printf("not able to push the element");

}

else

{

printf("Enter the value");

scanf("%d",&val);

if(head==NULL)

{

ptr->val = val;

ptr -> next = NULL;

head=ptr;

}

else

{

ptr->val = val;

ptr->next = head;

head=ptr;

}

printf("Item pushed");

}

void pop()

{

int item;

struct node *ptr;

if (head == NULL)

{

printf("Underflow");

}

else

{

item = head->val;

ptr = head;

head = head->next;

free(ptr);

printf("Item popped");

}

void display()

{

int i;

struct node *ptr;

ptr=head;

if(ptr == NULL)

{

printf("Stack is empty\n");

}

else

{

printf("Printing Stack elements \n");

while(ptr!=NULL)

{

printf("%d\n",ptr->val);

ptr = ptr->next;

}

Q7) What is Postfix Expression?

A7)

For solving a mathematical expression, we need prefix or postfix form. After converting infix to postfix, we need postfix evaluation algorithm to find the correct answer.

Here also we have to use the stack data structure to solve the postfix expressions.

From the postfix expression, when some operands are found, pushed them in the stack. When some operator is found, two items are popped from the stack and the operation is performed in correct sequence. After that, the result is also pushed in the stack for future use. After completing the whole expression, the final result is also stored in the stack top.

Input and Output

Input:

Postfix expression: 53+62/*35*+

Output:

The result is: 39

Algorithm

postfixEvaluation(postfix)

Input: Postfix expression to evaluate.

Output: Answer after evaluating postfix form.

Begin

for each character ch in the postfix expression, do

if ch is an operator ⨀ , then

a := pop first element from stack

b := pop second element from the stack

res := b ⨀ a

push res into the stack

else if ch is an operand, then

add ch into the stack

done

return element of stack top

End

Q8) What is Prefix Expressions?

A8)

Prefix and Postfix expressions can be evaluated faster than an infix expression. This is because we don’t need to process any brackets or follow operator precedence rule. In postfix and prefix expressions which ever operator comes before will be evaluated first, irrespective of its priority. Also, there are no brackets in these expressions. As long as we can guarantee that a valid prefix or postfix expression is used, it can be evaluated with correctness.

In this article, we will discuss how to evaluate an expression written in prefix notation. The method is similar to evaluating a postfix expression.

Algorithm

EVALUATE_PREFIX(STRING)

Step 1: Put a pointer P at the end of the end

Step 2: If character at P is an operand push it to Stack

Step 3: If the character at P is an operator pop two

elements from the Stack. Operate on these elements

according to the operator, and push the result

back to the Stack

Step 4: Decrement P by 1 and go to Step 2 as long as there

are characters left to be scanned in the expression.

Step 5: The Result is stored at the top of the Stack,

return it

Step 6: End

Example to demonstrate working of the algorithm

Expression: +9*26

Character | Stack | Explanation

Scanned | (Front to |

| Back) |

-------------------------------------------

6 6 6 is an operand,

push to Stack

2 6 2 2 is an operand,

push to Stack

* 12 (6*2) * is an operator,

pop 6 and 2, multiply

them and push result

to Stack

9 12 9 9 is an operand, push

to Stack

+ 21 (12+9) + is an operator, pop

12 and 9 add them and

push result to Stack

Result: 21

Q9) What are the Basic Operations of queue?

A9)

Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues −

enqueue()− add (store) an item to the queue.

dequeue()− remove (access) an item from the queue.

Few more functions are required to make the above-mentioned queue operation efficient. These are −

peek()− Gets the element at the front of the queue without removing it.

isfull()− Checks if the queue is full.

isempty()− Checks if the queue is empty.

In queue, we always dequeue (or access) data, pointed by front pointer and while enqueing (or storing) data in the queue we take help of rear pointer.

Let's first learn about supportive functions of a queue −

peek()

This function helps to see the data at the front of the queue. The algorithm of peek() function is as follows −

Algorithm

begin procedure peek

return queue[front]

end procedure

Implementation of peek() function in C programming language −

Example

int peek() {

return queue[front];

}

isfull()

As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function −

Algorithm

begin procedure isfull

if rear equals to MAXSIZE

return true

else

return false

endif

end procedure

Implementation of isfull() function in C programming language −

Example

bool isfull() {

if(rear == MAXSIZE - 1)

return true;

else

return false;

}

isempty()

Algorithm of isempty() function −

Algorithm

begin procedure isempty

if front is less than MIN OR front is greater than rear

return true

else

return false

endif

end procedure

If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty.

Here's the C programming code −

Example

bool isempty() {

if(front < 0 || front > rear)

return true;

else

return false;

}

Enqueue Operation

Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks.

The following steps should be taken to enqueue (insert) data into a queue −

Step 1− Check if the queue is full.

Step 2− If the queue is full, produce overflow error and exit.

Step 3− If the queue is not full, increment rear pointer to point the next empty space.

Step 4− Add data element to the queue location, where the rear is pointing.

Step 5− return success.

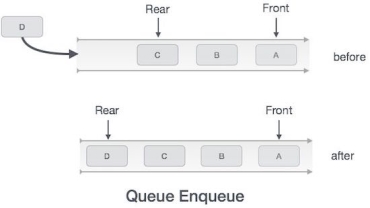
Insert Operation

Sometimes, we also check to see if a queue is initialized or not, to handle any unforeseen situations.

Algorithm for enqueue operation

procedure enqueue(data)

if queue is full

return overflow

endif

rear ← rear + 1

queue[rear] ← data

return true

end procedure

Implementation of enqueue() in C programming language −

Example

int enqueue(int data)

if(isfull())

return 0;

rear = rear + 1;

queue[rear] = data;

return 1;

end procedure

Dequeue Operation

Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation −

Step 1− Check if the queue is empty.

Step 2− If the queue is empty, produce underflow error and exit.

Step 3− If the queue is not empty, access the data where front is pointing.

Step 4− Increment front pointer to point to the next available data element.

Step 5− Return success.

Remove Operation

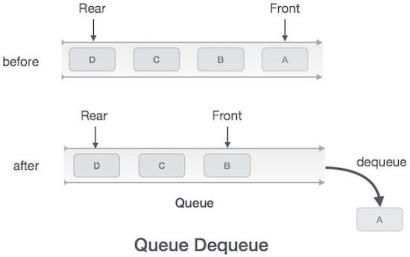
Algorithm for dequeue operation

procedure dequeue

if queue is empty

return underflow

end if

data = queue[front]

front ← front + 1

return true

end procedure

Implementation of dequeue() in C programming language −

Example

int dequeue() {

if(isempty())

return 0;

int data = queue[front];

front = front + 1;

return data;

}

Sign Up