Unit-2

Set Theory

Q1) Define set & how do we represent sets?

A1)

Sets- A set is a collection of well-defined objects which are called the elements or members of the set.

We generally use capital letters to denote sets and lowercase letters for elements.

If any element which exists in the set is to be denoted as-

Suppose an element ‘a’ is from a set X, then it is represented as- aX

Which means the element ‘a’ belongs to the set X.

If the element is not form the group then we use ‘not belongs to’.

Representation of sets-

There are two ways to represent sets.

1. In first way, the elements of the set are separated by comma and contained in the bracket-{  }.

2. The second way is that we define the characteristic of the element.

For example-

Suppose we have a set ‘A’ of all odd integers which are greater than 3.

Then we can represent it two ways-

1. A = {5, 7, 9…….}

2. A = {x | x is an odd integer, x>3 }

Q2) Define union and intersection.

A2)

1. Union and intersection-

Union-We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B.

That is-

                                       A∪B = {x |x∈∅A or x∈∅B}

Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.

That is-

                                        A∩B = {x |x∈∅A and x∈∅B }

Note- Two sets are said to be disjoint if they have no common elements in common.

Q3) If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}

A3)

Then-

A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}

A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}

B∪C = {4, 5, 6,7, 8, 9, 10}

A∩B = {4, 5, 6}

A∩C = {5, 6}

B∩C = {5, 6, 7, 8, 9}

Q4) Define cardinality of sets.

A4)

Cardinality of sets-

If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].

Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4

Cardinality of union of two sets-

Number of elements in A ∪B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |

Q5) What do you understand by the principle of inclusion and Exclusion.

A5)

Principal of inclusion and Exclusion-

Let we have A andB are finite sets. Then A ∪B and A ∩B are

Finite and

n(A ∪B) = n(A) + n(B) −n(A ∩B)

That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then

Subtracting n(A ∩B) (exclusion) since its elements were counted twice

For three sets-

n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)

Q6) Define ordered pair.

A6)

Ordered pair-

An ordered pair of element a and b, where a is designated as the first element and b as the second element, it is denoted by (a, b).

In particular

If and only if a = c and b = d. thus
 

Unless a = b.

Q7) Define Cartesian product.

A7)

Suppose we have two sets A and B, then we can form the set-

To be the set of all ordered pairs (x,y) where x is an element of A and y is an element of B.

Here we call the Cartesian product of A and B.

Q8) Let A = {1, 2} and B = {a, b, c}, then-

A8)

Q9) If A, B, C are sets then prove that-

A9)

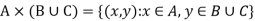
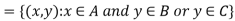
Q10) Define Complements, differences and symmetric differences.

A10)

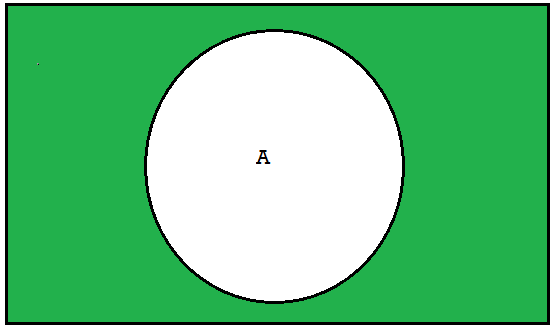
Complement-

The complementof a set A, denoted by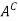 , is the set of elements which belong to U(universal set)but which do not belong to A. That is

= {x | x ∈U, x /∈A}

Difference-

The differenceof A and B, denoted byA\B or A-B, is the set of elements which belong to A but which do not belong to Bthat is-

A-B = {x | x ∈A, x / ∈B}

The set A\Bor A-Bis read “A minus B”.

Symmetric difference-

The symmetric differenceof sets A and B, denoted by A⊕B, consists of those elements which belong to A or B but not to both. That is

A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)