Unit-5
Lattice & Boolean algebra
Q1) Define lattices.
A1)
Lattices-
A lattice is a partially ordered set  in which every pair of elements a,b
in which every pair of elements a,b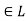 has a greatest lower bound and a least upper bound
has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S);  that means (
that means ( is partially ordered.
is partially ordered.
If X and Y are two elements of L, then-

Hence ( is a Lattice.
is a Lattice.
Q2) Let (L, ≤) be a lattice in which ‘⋅’ And ‘+’ denote the operations of meet and join respectively.
Then
a≤b ⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
A2)
Suppose a ≤b
As we know that a ≤a so that a ≤a.b but according to definition a.b≤a
So that- a ≤b ⇒a ⋅b = a
Let a ⋅b = a
But this is possible only if a ≤b which means a ⋅b = a ⇒a ≤b
∴a≤b⇒a ⋅b = a and a ⋅b = a ⇒a ≤b
Combine these two, we get
a≤b ⇔a ⋅b = a
Now let,
a⋅b = a,
Then we have
b + (a ⋅b) = b + a + a + b
But,
b + (a ⋅b) = b
Hence a + b = b
Similarly by assuming a + b = b
We can show that a ⋅b = a
Hence a ≤b ⇔a ⋅b = a ⇔a + b = b = a
Q3) Define isomorphic lattice.
A3)
Isomorphic Lattice-
Two lattices L and L’are said to be isomorphic if there is a one-to-one correspondence
f: L →L’
Such that
f (a ∧b) = f (a) ∧f (b) and f (a ∨b) = f (a) ∨f (b)
For any elements a, b in L.
Q4) What is direct product?
A4)
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Q5) Define distributive lattice.
A5)
A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
Note- The power set of a non-empty set A is a lattice under the operation ∩and ∪is a distributive lattice.
Q6) Define Boolean algebra.
A6)
A Boolean algebra is a distributive complemented lattice having atleast two elements as well as 0 and 1.
A Boolean algebra is generally denoted by a 6-tuple, (B, +, ⋅, 1, 0, 1) where (B, +, ⋅) is a lattice with two binary operations + and ⋅, called the join and meet respectively is a unary operation in B. The elements 0 and 1 are the least and greatest elements of the lattice (B, +, ⋅). The following axioms are satisfied:
1. There exist at least two elements a, b in B and that a ≠b.
2. ∀a, b ∈B
(i) a+ b ∈B
(ii) a⋅b ∈B
3. for all a, b ∈B
(i) a+ b = b + a
(ii) a⋅b = b ⋅a
Commutative laws
4. Associative laws: for all a, b, c ∈B
(i) a+ (b + c) = (a + b) + c
(ii) a⋅(b ⋅c) = (a ⋅b) ⋅c
5. Distributive laws: for all a, b, c ∈B
(i) a+ (b ⋅c) = (a + b) ⋅(a + c)
(ii) a⋅(b + c) = (a ⋅b) + (a ⋅c)
6. (i) Existence of zero: There exists of B such that
a + 0 = a ∀a ∈B
The element 0 is called the zero element
(ii) Existence of unit: There exists 1 ∈B sum that
a⋅1 = a ∀a ∈B
The element 1 is called the unit element.
7. Existence of complement: ∀a ∈B there exists an element a′∈B such that
(i) a+ a′ = 1 and (ii) a ⋅a′ = 0
Q7) Define equivalent Boolean expression.
A7)
Two Boolean expression α( ) and β(
) and β( ) are said to be equivalent if one can be obtained from the other by a finite number of application of the identities of Boolean algebra.
) are said to be equivalent if one can be obtained from the other by a finite number of application of the identities of Boolean algebra.
Q8) Simplify z (y+z) ((x + y + z).
A8)
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Q9) Simplify Y = (P + Q) (P + Q′) (P′+ Q)
A9)
Y = (P + Q) (P + Q′) (P′+ Q)
= (P P+ P Q′+ P Q + Q Q′) (P′+ Q)
= (P + P Q′+ P Q + 0) (P′+ Q)
= (P + P Q′+ P Q) (P′+ Q)
= P P1 + P Q + P Q′P′+ P Q′Q + P Q P′+ P Q Q
= 0 + P Q + 0 + 0 + 0 + P Q
= P Q + P Q
= P Q
Q10) Minimize the expression  +
+ + A B
+ A B
A10)
 +
+  + A B
+ A B
=  +
+  +
+  + A B
+ A B
=  +
+  +
+ 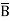 + A B
+ A B
=  +
+  + A B
+ A B
= 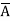 + A B +
+ A B + 

Hence