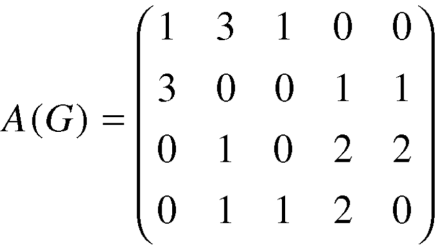Unit-6

Graph Theory

Q1) Define graph theory.

A1)

Graph theory is a relatively new area of mathematics

Graph is the form of representing of descriptive data in the terms of verticals and edges.

Graph theory is used in various fields like computer science, information technology, genetics, telecommunication etc.

A graph is a collection of vertices and edges in which each edge is assigned to pair of points called terminal.

We can say that a graph is a network of dots connected by lines.

Mathematically we can define a graph as-

A graph is a pair of set (V, E) where-

1. V is a non-empty set whose elements are called vertices.

2. E is collection of two-element subset of V called edges.

Q2) Consider the graphs given below-

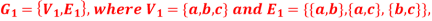
 Check whether these graphs are same or not?

A2)

As we can see that these graphs are not same because here and are not same since 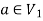but a does not belongs to .

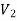These two graphs look same but not equal.

We can draw these graphs as below-

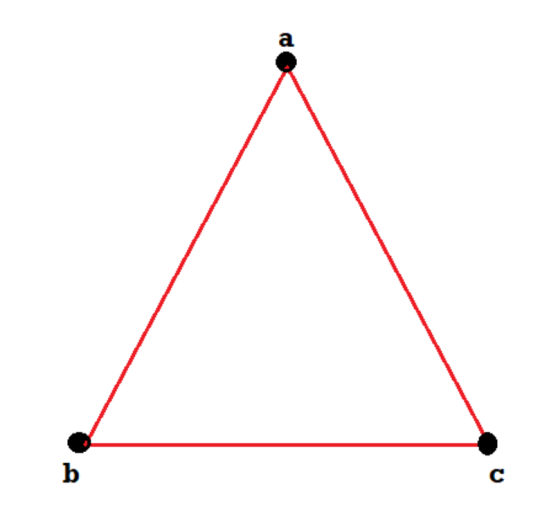
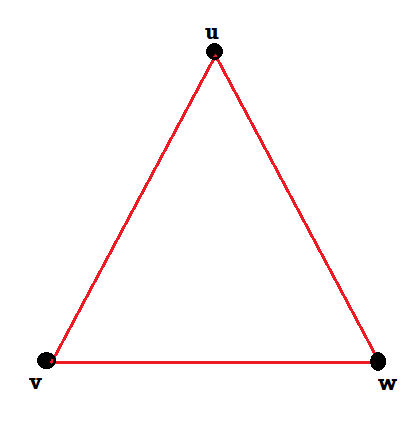
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.

Q3) Define degree of vertex.

A3)

Degree of vertex: The number of edges incident on a vertex v is called degree of vertex v, with loop being counted twice.

We can denote it as-

Degree of v = d(v)

Q4) What are the sub-graphs & isomorphic graph?

A5)

Sub-graph

We can say that 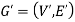is a sub-graph of G = (V, E), and write 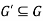provided .

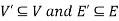We can say that 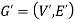is an induced sub-graph of G = (V, E), provided 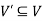and every edge in E whose vertices are still in 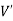is also an edge in .

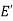Isomorphic graphs-

Let 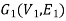and 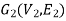be two graphs. The graph 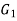and 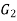are said to be isomorphic if there is a bijective function 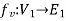such that if u and v are end vertices of some edge e ∈ 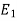then 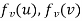end vertices of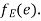

Q5) What are the applications of graph theory?

A5)

1. Graphs are used to define the flow of computation.

2. Graphs are used to represent networks of communication.

3. Graphs are used to represent data organization.

4. Graph transformation systems work on rule-based in-memory manipulation of graphs. Graph databases ensure transaction-safe, persistent storing and querying of graph structured data.

5. Graph theory is used to find shortest path in road or a network.

6. In Google Maps, various locations are represented as vertices or nodes and the roads are represented as edges and graph theory is used to find the shortest path between two nodes.

Q6) Define path and connectedness.

A6)

Paths-

Let G be a non-directed graph. A sequence P of zero or more edges of the form 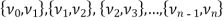, where 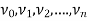are the vertices of G is called a path in G.

We denote this by P 

The vertex 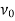is called the initial vertex and the vertex 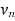is called the terminal vertex of the path P.

Connectedness-

Let G be a graph. Two vertices v and w of G are connected if, and only if, there is a walk from v to w. The graph G is connected if, and only if, given any two vertices v and w inG, there is a walk from v to w. Symbolically,

G is connected ⇔∀vertices v,w∈V(G), ∃a walk from v to w.

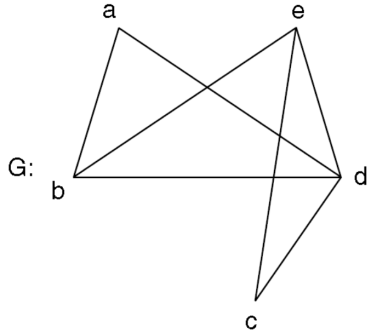
Q7) Find the adjacency matrix of the graph-

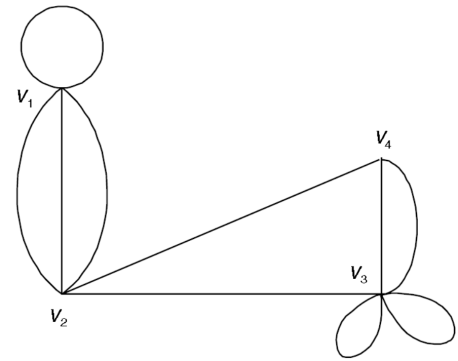
A7)

The adjacency matrix of the above graph will be-

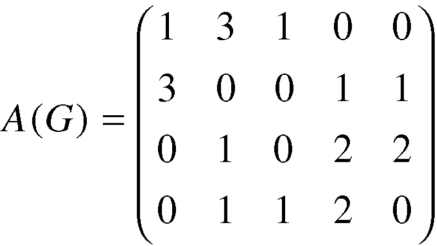
Q8) Define adjacency matrix of a non-directed graph.

A8)

Let G be a graph with n vertices and no parallel edges. The adjacency matrix of G in a n × n. symmetric binary matrix A (G) 

Where

Where 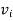and 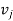are vertices of G.

The following is a example of the adjacency matrix of the simple graph G.

Adjacency matrix x; A (G)-

Q9) Define adjacency of a digraph.

A9)

Let G be a digraph with n vertices, containing non-parallel edges. The adjacency matrix A(G) of the digraph G is an n × n matrix defined by

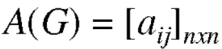
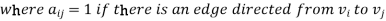
                  = 0 otherwise

Q10) Find the adjacency matrix of the graph-

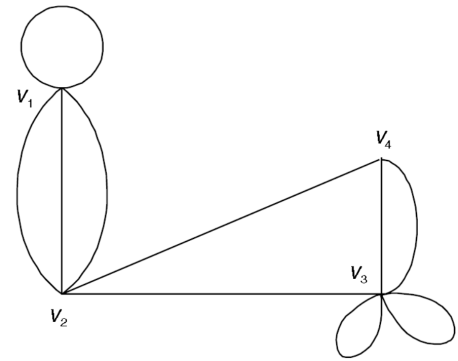
A10)

The adjacency matrix of the above graph will be-