undefined | unit 1 regular languages and finite automata

ALC

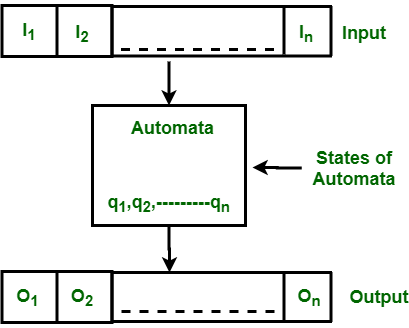
Unit 1Regular Languages and Finite Automata Q1) Write the application of FA?A1) Application of FA 1. Finite Automata (FA) –● Used in text editors.● For the implementation of spell checkers. 2. Push Down Automata (PDA) –● For designing the parsing phase of a compiler (Syntax Analysis).● For evaluating the arithmetic expressions. 3. Linear Bounded Automata (LBA) –● For implementation of genetic programming.● For constructing syntactic parse trees for semantic analysis of the compiler. 4. Turing Machine (TM) –● For implementation of neural networks and Robotics Applications.● For implementation of artificial intelligence. Q2) Define the finite automata?A2) Finite AutomataFinite Automata(FA) is the simplest pattern recognition machine. The finite automatic or finite state machine is an abstract machine with five components or tuples. It has a set of states and rules that switch from one state to another, but it depends on the input symbol that is added. It is essentially an abstract digital machine model. Some important features of general automation are shown in the figure below:

fig: features of finite automataThe figure above shows the following automated features:

Input

Output

State of automata

State relation

Output relation

A Finite Automata consists of the following: { Q, Σ, q, F, δ }. where,
Q : Finite set of states.Σ : set of Input Symbols.q : Initial state.F : set of Final States.δ : Transition Function. Q3) Write short notes on recursion?A3) Recursionrecursion is a very significant term. Using recursion will simplify many issues. A formal recursion description is a function that, after a finite number of steps, calls itself explicitly or indirectly and terminates. A well-defined recursive function should have the following properties, such that the program does not continue to run indefinitely: ● The base conditions for which the feature does not name itself must be present. ● The role has to be closer to the base criterion for any call to itself. A factorial, for example, can be recursively defined as: factorial(x) = x * factorial (x – 1) for x > 1= 1 for x = 1 or x = 0 The function's basic criteria are x = 1 or x = 0, i.e. When x = 1 or x = 0, the function does not call itself when it reaches x = 1 or x = 0. When x is not 1 or 0, the function calls itself and moves closer to the base criterion, since any recursive call reduces x. Q4) Write the difference between DFA and NDFA?A4) Difference between DFA and NDFA

DFA	NDFA
The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic.	The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic.
Empty string transitions are not seen in DFA.	NDFA permits empty string transitions.
Backtracking is allowed in DFA.	In NDFA, backtracking is not always possible.
Requires more space.	Requires less space.
A string is accepted by a DFA, if it transits to a final state.	A string is accepted by a NDFA, if at least one of all possible transitions ends in a Final state.

Q5) Describe regular expression and regular language?A5) ● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.● Regular languages are referred to as the languages recognized by certain regular expressions. ● A regular expression may also be defined as a pattern sequence that defines a series. ● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string. A Regular Expression can be recursively defined as follows − ● ε is a Regular Expression indicates the language containing an emptystring. (L (ε) = {ε})● φ is a Regular Expression denoting an empty language. (L (φ) = { })● x is a Regular Expression where L = {x}● If X is a Regular Expression denoting the language L(X) and Y is a Regular● Expression denoting the language L(Y), then

X + Y is a Regular Expression corresponding to the language L(X) ∪

L(Y) where L(X+Y) = L(X) ∪ L(Y).

X . Y is a Regular Expression corresponding to the language L(X) .

L(Y) where L(X.Y) = L(X) . L(Y)

R* is a Regular Expression corresponding to the language L(R*)

where L(R*) = (L(R))* ● If we apply any of the rules several times from 1 to 5, they are RegularExpressions. Unix Operator ExtensionsRegular expressions are used frequently in Unix: ● In the command line● Within text editors● In the context of pattern matching programs such as grep and egrep Additional operators are recognized by unix. These operators are used forconvenience only.● character classes: ‘[‘ <list of chars> ‘]’● start of a line: ‘^’● end of a line: ‘$’● wildcard matching any character except newline: ‘.’● optional instance: R? = epsilon | R● one or more instances: R+ == RR* Q6) What do you mean by union, intersection & complements of regular language?A6) Union and intersection Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection. Example of union: If L and M are regular languages, the same is true for L ∪ M. Proof: Let the languages of regular expressions R and S be L and M, respectively.Then R+S is a regular expression with L ∪ M as its language. Example of intersection:If L and M are regular languages, then L and M are identical. Proof: Let A and B be DFA's, respectively, whose languages are L ∩ M. Create C, an A and B product automaton. Make C's final states the pairs that consist of both A and B final states

fig : example of intersection Set complement Pick a DFA recognizing the language, then swap the accept/non- accept markings on its states. A language L supplement (with regard to an alphabet Σ such that Σ* Includes L) is Σ*-L. The complement of a regular language is often regular because Σ * is certainly regular. Q7) Define Deterministic and non - deterministic finite automata?A7): Deterministic finite automata In this, for each input symbol, the state to which the machine will move can bedetermined. As it has a finite number of states, the machine is called DeterministicFinite Machine or Deterministic Finite Automaton.An automaton can be represented by a 5-tuple (Q, ∑, δ, q 0 , F), where −Q is a finite set of states.∑ is a finite set of symbols, called the alphabet of the automaton.δ is the transition function.q 0 is the initial state from where any input is processed (q 0 ∈ Q).F is a set of final state/states of Q (F ⊆ Q). Non-deterministic Finite Automaton (NDFA)In NDFA, the machine can move to any combination of the states. Hence, it iscalled Non-deterministic Automaton as it has finite number of states. Q → Finite non-empty set of states.∑ → Finite non-empty set of input symbols.∂ → Transitional Function.q0 → Beginning state.F → Final State Q8) Construct an FA from RE?A8) Construct an FA from RE We begin by showing how to construct an FA for the operands in a regular expression. ● If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.● If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.● If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions. Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, andR1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2). ● The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.● The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF. ● The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF. Q9) How to convert NFA to DFA?A9) In NFA, the device goes to multiple states when a particular input is given to the current state. On a given input symbol, it can have zero, one or more than a move. On the other hand, in DFA, the program goes to only one state when a particular input is given to the current state. On a given input symbol, a DFA has only one move. Let, M = (Q, ∑, δ, q0, F) is an NFA which accepts the language L(M). There should be equivalent DFA denoted by M' = (Q', ∑', q0', δ', F') such that L(M) = L(M') Steps for Converting NFA to DFA - Step 1: Initially Q' = ϕStep 2: Add q0 of NFA to Q'. Then find the transitions from this start state.Step 3: In Q', find the possible set of states for each input symbol. If this set of states is not in Q', then add it to Q'.Step 4: In DFA, the final state will be all the states which contain F(final states of NFA) Q10) what is the simulation of DFA and NFA?A10) Let N = (QN , Σ, δN , qN0 , FN ) be a NFA. The equivalent DFA D1 is obtained from the so-called subset construction (also called “power construction”). We define D = (QD, Σ, δD, qD0 , FD),Where ● The alphabet of D is that of N. ● The states of D are sets of states of N: QD = P(QN )● The initial state qD0 of D is {qN0 }.● The final states of D are those sets that contain the final state of N: FD = {S ∈ P(QN )| S ∩ FN 6= ∅} ● The transition function of D arises from the transition function of N as follows: δD(S, a) = Uq∈S δN (q, a)That is, δD(S, a) is the set of all states of N that are reachable from some state q via a. Proposition. For every NFA N, there is a DFA D such that L(D) = L(N)

Sign Up