| unit 3 context free grammars

ALC

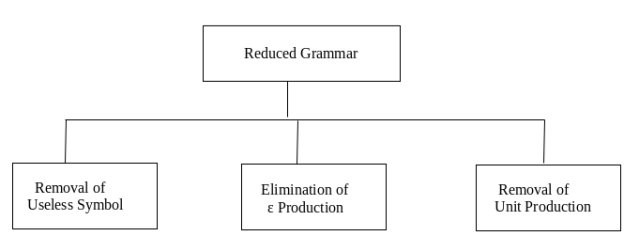
Unit 3Context free Grammars Q1) What do you mean by Context free grammar?A1) context free grammar Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns. It consists of:❏ a set of terminal symbols,❏ a set of non-terminal symbols,❏ a set of productions,❏ a start symbol.Context-free grammar G can be defined as:G = (V, T, P, S)Where G - grammar, used for generate string,V - final set of non-terminal symbol, which are denoted by capital letters,T - final set of terminal symbols, which are denoted be small letters,P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)S - start symbol, which is used for derive the stringA CFG for Arithmetic Expressions -An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:1. <expression> --> number2. <expression> --> (<expression>)3.<expression> --> <expression> +<expression>4. <expression> --> <expression> - <expression>5. <expression> --> <expression> * <expression>6. <expression> --> <expression> / <expression> The only non-terminal symbol in this grammar is <expression>, which is also thestart symbol. The terminal symbols are {+, -, *, /, (, ), number}

The first rule states that an <expression> can be rewritten as a number.

The second rule says that an <expression> enclosed in parentheses is also an <expression>

The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

Q2) Consider the following statements about the context free grammarG = {S->SS, S->ab, S->ba, S->ɛ}

G is ambiguous

G produces all strings with equal number of a’s and b’s

G can be accepted by a deterministic PDA

Which combination below expresses all the true statements about G?

I only

I and III only

II and III only

I, II and III

A2) There are different LMD’s for string abab which can beS =>SS =>SSS =>abSS =>ababS =>abab S => SS =>abS =>abab So the grammar is ambiguous. So statement I is true.Statement II states that the grammar G produces all strings with equal number of a’s and b’s but it can’t generate aabb string. So statement II is incorrect.Statement III is also correct as it can be accepted by deterministic PDA. So correct option is (B). Q3) what do you mean by Greibach Normal Form (GNF)?A3) Greibach Normal Form (GNF)If the productions are in the following forms, a CFG is in the Greibach Normal Form - A → bA → bD 1 …D nS → εwhere A, D 1, ...., D n are non-terminals and b is a terminal. Algorithm to Convert a CFG into Greibach Normal FormStep 1 − If the starting symbol S is on the right side, create a new starting symbol. S 'symbol and a new S'→ S output.Step 2 − Remove Null productions.Step 3 − Remove unit productions. Step 4 − Delete both left-recursion direct and indirect.Step 5 − To transform it into the proper form of GNF, make proper output substitutions. Example: Convert the following CFG into CNFS → XY | Xn | pX → mX | mY → Xn | oSol:Here, S does not appear on the right side of any production and in the production rule collection, there is no unit or null output. So, we'll be able to bypass step 1 to step 3.Step 4 -Now after replacingX in S → XY | Xo | pwithmX | mwe obtainS → mXY | mY | mXo | mo | p.And after replacingX in Y → X n | owith the right side ofX → mX | mwe obtainY → mXn | mn | o. The production set is added to two new productions O → o and P → p and then we arrived at the final GNF as the following - S → mXY | mY | mXC | mC | pX → mX | mY → mXD | mD | oO → oP → p Q 4) what is the simplification process?A4) simplification processAs we have included a context-free grammar can effectively represent different languages. Not all grammar is always optimized, which means that there might be some extra symbols in the grammar (non-terminal). Unnecessary change in the length of grammar with additional symbols. Here are the properties of reduced grammar:

Every parameter (i.e. non-terminal) and every terminal of G occurs in the derivation of any word in L.

As X→Y where X and Y are non-terminal, there should not be any output.

If ε is not in the L language, then the X→ ε output does not have to be.

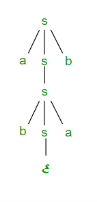
Let’s see the simplification process Fig.: Simplification process

 Removal of Useless Symbols - A symbol can be useless if it does not appear on the right-hand side of the production rule and is not involved in the derivation of any string. The symbol is regarded as a symbol which is useless. Likewise, if it does not participate in the derivation of any string, a variable may be useless. That variable is called a useless symbol.

 Elimination of ε Production - The Type S → ε productions are called ε productions. Only those grammars which do not produce ε can be excluded from these types of output.

Step 1: First find out all null able non-terminal variables which derive ε.Step 2: Create all output A → x for each production A →a where x is extracted from a by removing one or more non-terminals from step 1. Step 3: Now combine with the original output the outcome of step 2 and delete ε productions.

another non-terminal generates a non-terminal one.

To remove production unit, follow given steps: →Step 1: To delete X → Y, when Y→ a occurs in the grammar, apply output X → a to the grammar law. Step 2: Remove X → Y from the grammar now.Step 3: Repeat steps 1 and 2 until all unit output is deleted. Q5) Write short notes on derivation tree?A5) Derivation treeSuppose we have a context free grammar G with production rules: S->aSb|bSa|SS|ɛ Left most derivation (LMD) and Derivation Tree: Leftmost derivation of a string from staring symbol S is done by replacing leftmost non-terminal symbol by RHS of corresponding production rule. For example: The leftmost derivation of string abab from grammar G above is done as: S =>aSb =>abSab =>ababThe symbols in bold are replaced using production rules. Derivation tree: It explains how string is derived using production rules from S and is shown in Figure.

Ambiguity in Context free Grammar and Context free Languages

Figure Derivation tree Right most derivation (RMD): It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.For Example: The rightmost derivation of string abab from grammar G above is done as: S => SS =>SaSb =>Sab =>aSbab =>ababThe symbols in bold are replaced using production rules. The derivation tree for abab using rightmost derivation is shown in Figure.

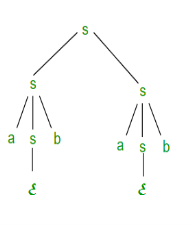
Ambiguity in Context free Grammar and Context free Languages2

Figure Right most derivation A derivation can be either LMD or RMD or both or none. For Example:S =>aSb =>abSab =>abab is LMD as well as RMD butS => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD. Q6) What do you mean by ambiguous CFG and ambiguous CFL?A6)Ambiguous context free grammar● A context free grammar is called ambiguous if there exists more than one LMD or RMD for a string which is generated by grammar. ● There will also be more than one derivation tree for a string in ambiguous grammar. ● The grammar described above is ambiguous because there are two derivation trees. ● There can be more than one RMD for string abab which are: S => SS =>SaSb =>Sab =>aSbab =>abab S =>aSb =>abSab =>abab Ambiguous Context Free Languages: A context free language is called ambiguous if there is no unambiguous grammar to define that language and it is also called inherently ambiguous Context Free Languages. Q7) Write short notes on Chomsky Normal Form (CNF)?A7) Chomsky Normal Form (CNF)The Chomsky normal form (CNF) is a context free grammar (CFG) if all output rules satisfy one of the conditions below:

A non-terminal generating a terminal (e.g.; X->x)

A non-terminal generating two non-terminals (e.g.; X->YZ)

Start symbol generating ε. (e.g.; S->ε)

Consider the following grammars,G1 = {S->a, S->AZ, A->; a, Z->z}G2 = {S->a, S->aZ, Z->a}As production rules comply with the rules defined for CNF, the grammar G1 is in CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF. Q8) Remove the production from the given CFG

E → XYX

X → 0X | ε

Y → 1Y | ε

A8)Now, we remove the rules X → ε and Y → ε while removing ε production. In order to maintain the sense of CFG, whenever X and Y appear, we actually position ε on the right-hand side. Let’s see If the 1st X at right side is ε, thenE → YX Similarly, if the last X in right hand side is ε, thenE → XY If Y = ε, thenE → XX If Y and X are ε then,S → X If both X are replaced by εE → Y Now,E → XY | YX | XX | X | Y Now let us considerX → 0X If we then put ε for X on the right-hand side,X → 0 X → 0X | 0 Similarly, Y → 1Y | 1Collectively, with the ε output excluded, we can rewrite the CFG asE → XY | YX | XX | X | Y X → 0X | 0 Y → 1Y | 1 Q9) Convert the following CFG into CNFS → XY | Xn | pX → mX | mY → Xn | o A9) Here, S does not appear on the right side of any production and in the production rule collection, there is no unit or null output. So, we'll be able to bypass step 1 to step 3.Step 4 -Now after replacingX in S → XY | Xo | pwithmX | mwe obtainS → mXY | mY | mXo | mo | p.And after replacingX in Y → X n | owith the right side ofX → mX | mwe obtainY → mXn | mn | o. The production set is added to two new productions O → o and P → p and then we arrived at the final GNF as the following - S → mXY | mY | mXC | mC | pX → mX | mY → mXD | mD | oO → oP → p Q10) What is the union, concatenation and Kleene’s of CFL?A10) Union Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free. ExampleLet A1 = { xn yn , n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|abLet A2 = { cm dm , m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| εUnion of A1 and A2 , A = A1 ∪ A2 = { xn yn } ∪ { cm dm } The corresponding grammar G will have the additional production S → S1 | S2 So under Union, CFLs are closed.

ConcatenationIf A1 and A2 are context free languages, then A1 A2 is also context free. Example Union of the languages A1 and A2 , A = A1 A2 = { anbncmdm }The additional development would have the corresponding grammar G, P: S → S1 S2 So under Concatenation, CFL are locked . Kleene StarIf A is a context free language, so that A* is context free as well . Example Let A = { xn yn , n ≥ 0}. G will have corresponding grammar P: S → aAb| εKleene Star L 1 = { xn yn }* The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε So under Kleene Closure, CFL's are closed.

Sign Up