undefined | unit 6 turing machines

ALC

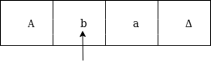
Unit-6Turing Machines Q1) Describe TM as language acceptor?A1) TM as language acceptorEven though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements. Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM. Example: Creating a turing machine which accepts the language of aba over ∑ = {a, b}Sol: We'll think that the string 'aba' is positioned like this on the input tape:

The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop. Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:

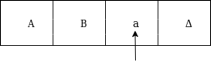
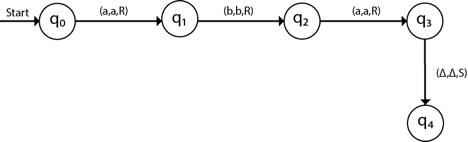
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and head moves toward right :

The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and head moves toward right :

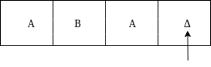
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and head moves toward right :

The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .

State	a	b	ᇫ
q0	(q1, A, R)	-	-
q1	-	(q2,B,R)	-
q2	(q3,A,R)	-	-
q3	-	-	(q4, ᇫ , S)
q4	-	-	-

The turing machine can be represented by transition diagram -

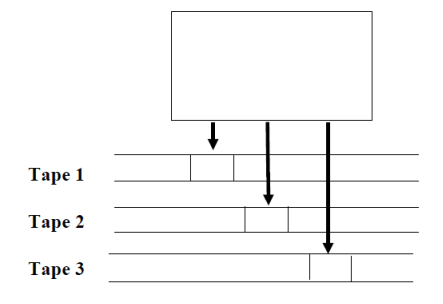
Q2) Define multitape TM ?A2) Multitape TM

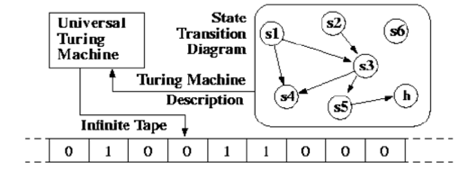
– Initially,• the input string is placed on the 1st tape;• the other tapes hold all blanks;• the finite control is in its initial state;• the head of the 1st tape is at the left end of the input;• the tape heads of all other tapes are at arbitrary positions. – A move consists of the following steps:• the finite control enters a new state;• on each tape, a symbol is written;• each tape head moves left or right, or stationary. Q3) What is universal TM?A3) Universal TMA Turing Machine is the mathematical tool equivalent to a digital computer. It wassuggested by the mathematician Turing in the 30s, and has been since then themost widely used model of computation in computability and complexity theory.The model consists of an input output relation that the machine computes. The inputis given in binary form on the machine’s tape, and the output consists of the contentsof the tape when the machine halts. What determines how the contents of the tape change is a finite state machine (orFSM, also called a finite automaton) inside the Turing Machine. The FSM isdetermined by the number of states it has, and the transitions between them. At every step, the current state and the character read on the tape determine thenext state the FSM will be in, the character that the machine will output on the tape(possibly the one read, leaving the contents unchanged), and which direction thehead moves in, left or right. The problem with Turing Machines is that a different one must be constructed forevery new computation to be performed, for every input output relation. This is why we introduce the notion of a universal turing machine (UTM), whichalong with the input on the tape, takes in the description of a machine M. The UTMcan go on then to simulate M on the rest of the contents of the input tape. A universal turing machine can thus simulate any other machine.

Q4) What do you mean by Computing partial function with a TM ?A4) Computing partial function with a TMBeing a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined. δ(non-halting-state, symbol) = UNDEFBy adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission δ(R,σ) = (R,σ) ∀ σ ∈ ΣSimply send a missing transition to this state without tape modification with this addition, i.e., δ(non-halting-state, symbol) = (R, symbol)The easiest computer we can create that runs indefinitely is this: RunForever = ( {s,h}, Σ, {}, s, {h} )There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever" Q5) What are the Techniques for Turing Machine Construction?A5) Techniques for Turing Machine ConstructionThere is some technique for turing machine, which are - ● Storage in finite controlTechnique: - Using the finite control of a TM to hold a finite amount of data, in addition to the state. Method: - Assuming the state as [q, A, B, C], for example, when the finite control holds three data elements A, B, and C. Example: Design a TM to recognize 01* + 10*. The set of states are of the form [qi, X] where qi = q1, q2; X = 0, 1, B. • The control portion (state) remembers what the TM is doing (q0 = not read 1st symbol; q1 = reverse). • The data portion remembers the first symbol seen (0, or 1). The transition function d is as follows.• d([q0, B], a) = ([q1, a], a, R) for a = 0, 1. --- Copying the symbol it scanned.• d([q1, a],a) = ([q1, a],a, R) wherea is the complement of a = 0, 1. --- Skipping symbols which are complements of the 1st symbol read (stored in the state as a).• d([q1, a], B) = ([q1, B], B, R) for a = 0, 1. --- Entering the accepting state [q, B] when reaching the 1st blank. ● Multi tracksAssuming the tape of a TM as composed of several tracks.For example, if there are three tracks, we use the tape symbol as [X, Y, Z]Example The TM recognizes the non-CFL languageL = {wcw | w is in (0 + 1)+}.● Checking off symbolsWe use one tape track to indicate that some symbols have Without modifying them, they are read. Example: Consider a Turing machine for accepting w#w#w, w ∈ {a, b}∗ Sol: A tape considered is two tracks. When the TM reads the first a in state q0, it stores it by taking the state as a pair) in its memory, checks off 'a by printing a 'in the second track below a, moves right and checks if the symbol is a' a 'after the # symbol. If it is marked by putting a a √ in the second direction, it moves correctly and The first symbol checks again after # is a 'a' and it also labels if so. For each unmarked, it then moves left and repeats the process in each block, the leftmost symbols. The computer stops accepting the string if all the symbols in the first block match the second and third blocks. Q6) A turing machine that is able to simulate other turing machines: a) Nested Turing machinesb) Universal Turing machinec) Counter machined) None of the mentioned A6) correct answer is “b “. Explanation: The Church and Turing together, called the Church-Turing thesis, proposed a more mathematically based concept with the same universal nature (formal theory of computation).

Sign Up