UNIT 1

INTRODUCTION

Q1) What is algorithm? Explain in brief?

A1)

Basically algorithm is the finite steps to solve problem in computer.

It can be the set of instruction than performs certain task.

The collection of unambiguous instruction occurring in some specific sequence and such a procedure should produce output for a given set of input in finite amount of time is known as Algorithm.

Q2) Explain the algorithm with its specifications?

A2)

Q3) Explain asymptotic notations in brief. It is formal way to speak about functions and classify them?

A3)

It is used to specify the running time and space complexity of algorithm and to frame the run time performance in mathematical computation.

It refers as foundation or framing into the mathematical terms.

As the algorithm having three cases according to time taken by program to perform a certain task.

Following are the asymptotic notations which are used to calculate the running time complexity of algorithm:

Q4) Explain big oh asymptotic notation with its analysis?

A4)

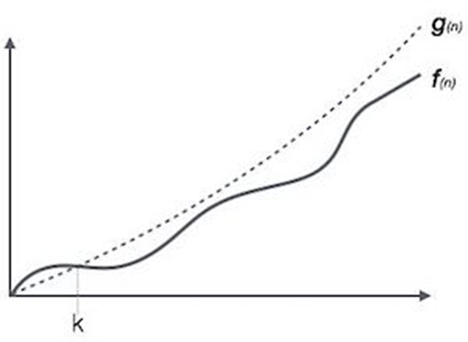
Here, f( n ) <= g( n ) ……………..(eq1)

            where n>= k , C>0 and k>=1

if any algorithm satisfies the eq1 condition then it becomes f ( n )= O  ( g ( n ) )

Q5) Explain big omega asymptotic notation with its analysis?

A5)

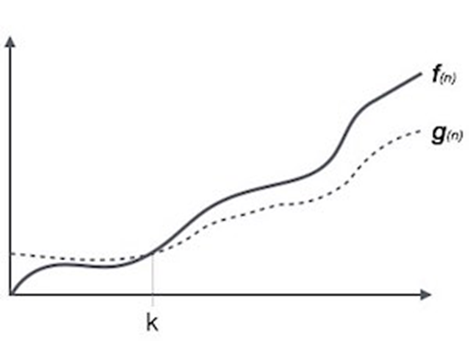
Here, f ( n ) >= g ( n )

where n>=k and c>0, k>=1

if any algorithm satisfies the eq1 condition then it becomes f ( n )= ῼ ( g ( n ) )

Q6) Explain big theta asymptotic notation with its analysis?

A6)

Let C1 g(n) be upper  bound and C2 g(n) be lower bound.

C1 g(n)<= f( n )<=C2 g(n)

Where C1, C2>0 and n>=k

Q7) Explain Heap Data Structure?

A7)

Heap is the special tree based data structure in which it has to satisfy the condition of complete binary tree.

Following are two types of heap:

Max-heap: in this key present at root node must be greater among all key present at all of its children.

Min-heap: in this key present at root node must be minimum among all key present at all of its children.