undefined | unit 5 backtracking

UNIT 5

BACKTRACKING

Q1) Write short note on backtracking?

A1)

It is a general algorithmic technique.

Backtracking algorithm is used to solve a problem recursively to get a solution incrementally.

It is used to solve problem in sequence of object is chosen from a specified set so that the sequence can satisfy some criteria.

Backtracking is the systematic method which helps to trying out a sequence of decision until you find out that solution.

It starts with one smaller piece at a time, if its solution get fail to satisfy the constraint then it can remove at any point of time.

It searches for any possible combination in order to solve a computational problem.

Two constraints :

Implicit constraint

Explicit constraint

Application:

N-queen problem

Sum of subset

Graph coloring

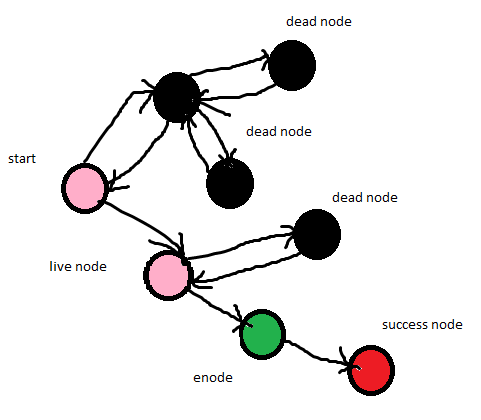
Q2) Explain 8-Queen problem with algorithm?

A2)

The eight queens problem is the problem of placing eight queens on an 8×8 chessboard such that none of them attack one another.

The eight queen puzzle has 92 distinct solutions.

If solution that differs only by symmetry operation of the board are counted as one puzzle has 12 unique solution.

Formulation of problem:

States: any arrangement of 8 queens on board

Initial state: 0 queens on the board

Successor function: add a queen on any square

Goal state: unattacked 8 queens on the board

Steps to be perform:

Place the first queen in the left upper corner of the table

Save the attacked position

Move to the next queen which can only placed on next line

Search fopr a valid position.(unattackled position) If there is one go to step 8.

There is not a valid postion for a queen then delete it.

Move to the previous queen

Got o step 4

Place it to the first valid position

Save the attacked postions

If the queen processed is the last stop otherwise go to step 3.

Algorithm:

Solution:

putQueen(row)

{

For every position col on the same row

If the position col is available

Place the next queen in position col

If(row<8)

putQueen(row+1)

else success

remove the queen from positioncol

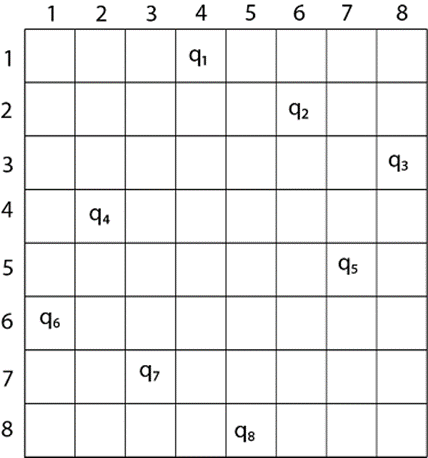
Q3)Analyse the sum of subset with example?

A3)

In this problem there is given set with integer numbers and also some another values provided. We have to find a subset of given set whose sum is same as given sum value.

Here backtracking is used for trying to select a valid subset when a number is not valid. We will backtrack to get the previous subset and add other number to get solution.

In backtracking algorithm as we need to explore the nodes along the breadth and depth of tree.

Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion.

This problem based on post order traversal method.

Following are the steps to solve the problem:

Step 1: start with an empty set

Step 2: Add element from given list to the set

Step 3: If the set is having sum M then stop with that subset as solution

Step 4: if the set is not feasible then backtracks until we find the solution.

Step 5: If the set is feasible and sum of subset < M then go to step 2

Step 6: if we have visited all numbers given in set without finding suitable solution and if no backtrack is possible then stop.

Example:

Given set of numbers= {1,3,2,4}

Find subsets with sum=3

Step 1: consider an empty set { }

Add 1 into empty set { 1 } (sum=1,1<3)

Add 3 into set {1,3} (sum=4,4>3,backtrack)

Remove 3 from subset { 1 }

Add 2 into set { 1,2 } (sum=3,3=3,found solution)

We remove 2 and check all elements have been considered.

Solution: { }  {1}  {1, 3}(backtrack) {1}  {1,2 }(found) {1}(end)

Q4) Write short note on knapsack problem with example?

A4)

In 0/1 knapsack algorithm we have given set of items with weights and profit.

The container of fixed capacity and are required to compute a loading of knapsack with items such that total profit is maximised.

We have only 1 of each item hence there is either 0 or 1 of each item in the knapsack hence it is named as 0/1 knapsack problem.

0/1 knapsack problem can be solve efficiently using backtracking.

Example:

Let 4 items are given.

W=8

Weight	2	3	4	5
profit	3	5	6	10

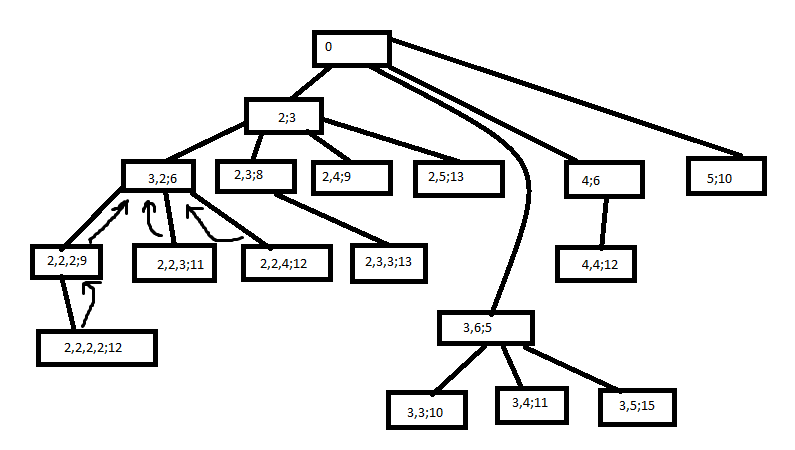
Selected weights are: 3 and 5

Maximum profit: 5+10=15

Q5) Analyse the Hamilton Cycle?

A5)

Hamilton path is the path from first vertex to last vertex which visits each vertex exactly once in undirected or directed graph.

Hamilton cycle is the circuit in which there is an edge from the last vertex to first vertex.

In this problem we can determine whether graph contains a Hamilton cycle or not. If the cycle presents then it prints the cycle.

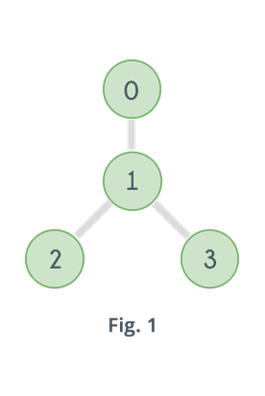
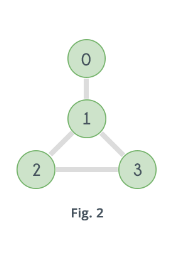
enter image description here

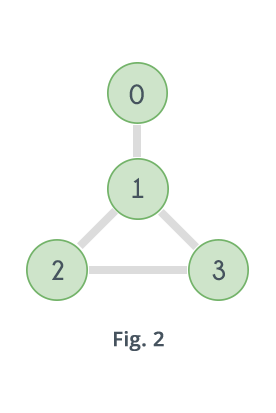
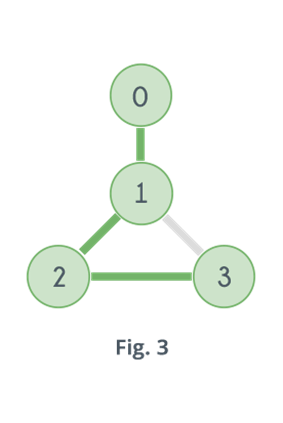
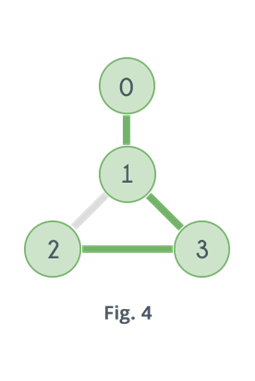
Q6) Analyse Graph Coloring Algorithm with example?

A6)

In this problem we have given the graph and asked to color all vertices with n given colours in such a way that no two adjacent vertices should have the same colour.

The least possible value of n required to colour the graph successfully is known as the chromatic number of given graph.

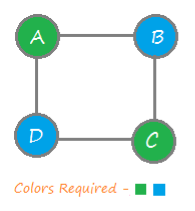
Graph coloring problem

Steps to color graph:

Step 1: start with coloring single vertex

Step 2: move to its adjacent vertex and use that which is not used by its connecting vertex. If no color is available then backtracks ie. Un-color the last colored vertex and return false

Step 3: Repeat step 2 until all vertices of given graph are colored.

Step 4: if we find the vertex is uncoloured and its adjacent are colored with different colors and no color is available for current vertex then we need more colors ie. Bigger chromatic number.

Example:

Sign Up