undefined | unit 5 intermediate code generation

Back to Study material

Unit - 5Intermediate Code Generation Q. 1) Explain procedure call ?Ans : Procedure Call● Procedure for a compiler is a significant and widely used programming construct. It is used to produce good code for calls and returns for processes. ● The run-time routines that manage the passing, calling and returning of procedure arguments are part of the packages that support run-time. Calling sequence :A series of acts taken on entry and exit from each procedure is part of the translation for a call. In the calling sequence, the following actions take place: ● When a procedure call occurs, space for the activation record is allocated. ● Review the so-called method statement. ● Develop environment pointers to allow data in enclosing blocks to be accessed by the named procedure. ● Save the state of the calling process so that after the call it can restart execution.● Save the return address as well. It is the address of the place to which, after completion, the so-called routine must be moved. ● Finally, the call procedure creates a hop to the beginning of the code.let us consider a grammar for a simple procedure call statement● S call id (Elist)● Elist Elist, E● Elist EFor the procedure call, an appropriate transfer scheme would be:

Production rule	Semantic action
S → call id(Elist)	for each item p on QUEUE do GEN (param p) GEN (call id.PLACE)
Elist → Elist, E	append E.PLACE to the end of QUEUE
Elist → E	initialize QUEUE to contain only E.PLACE

In the procedure call, the queue is used to store a list of parameters. Q. 2) What do you mean by assignment statement ?Ans : Assignment Statement Assignment statements allow a symbol to be specified or redefined by the programmer by assigning it a value. This value may be a reference to a different symbol, name of the register, or expression. The new value automatically takes place and remains in effect until the symbol has been redefined. There are no forward connections to symbols specified in assignment statements. Furthermore, symbols specified in assignment statements are unable to:

● The symbol table of the output object file appears.

● Global be declared.

● In an equivalent sentence, be described.

Two types of assignment statements exist:

● Symbol assignment statements, Defining or redefining a symbol in the namespace of a symbol.

● Register assignment statements, Defining or redefining the name of the register in the symbol name space.

Symbol assignment statements

The following syntax is available for a symbol assignment statement:identifier = expression // commentsWhere, Identifier = Represents a symbol inside the namespace of the symbol.Expression = Specifies the identifier's form and meaning. The term cannot contain references forward.An example of an assignment statement that describes a symbol is below:S = B0+2

2. Register assignment statements

The following syntax is available for a register assignment statement:identifier = register name // commentsWhere, Identifier = Represents the name of a register in the name space of the symbol.Register name = Specifies the name of the alternative register. If the name of the register is a stack or a revolving register name, the current name of the register continues to refer to the previously specified name of the register, even if the name is no longer valid. An example of an assignment statement that specifies a name for a register is as follows:B = p1 Q. 3) Describe a case statement ?Ans : Case Statement In a number of languages, the "switch" or "case" statement is available. The syntax for switch-statement is as shown below: Switch-statement syntax s with expressionbegin case value : statementcase value : statement.. case value : statementdefault : statementendThere is a selector expression to be evaluated, followed by n constant values that may be taken by the expression, including a default value that, if no other value does, always matches the expression. Code to: is the intended translation of a turn. 1. Assess an expression. 2. Find which value is equivalent to the value of the expression in the list of cases.3. Conduct the assertion that is correlated with the found meaning. Find the following paragraph about the switch: switch Ebegin case V1 : S1 case V2 : S2 case Vn-1 : Sn-1default : Sn endThis case statement is translated into an intermediate code in the following form: Translation of a case statement. code to analyze E into t goto testgoto TEST L1: code for S1 goto NEXT L2: code for S2 goto NEXT . . . Ln-1: code for Sn-1 goto NEXT Ln: code for Sn goto NEXT TEST: if T = V1 goto L1 if T = V2 goto L2 . . . if T = Vn-1 goto Ln-1 goto NEXT: A new temporary T and two new label tests are created when the switch keyword is seen, and next. When the case keyword happens, a new label Li is generated and inserted into the symbol table for each case keyword. A stack is put with the Vi value of each case constant and a pointer to this table-symbol entry. Q. 4) Write something about declaration ?Ans : Declaration We need to lay out storage for the declared variables when we encounter declarations. You can manage declaration with a list of names as follows :D T id ; D | εT B C | record ‘{‘D’}’B int | floatC ε | [ num ] C ● A declaration sequence is generated by Nonterminal D. ● A fundamental, array or record form is generated by nonterminal T. ● One of the basic int or float types is generated by nonterminal B. ● Nonterminal C produces a string of zero or more integers, each surrounded by brackets for "component". We create a ST(Symbol Table) entry for every local name in a procedure, containing: ● The type of the name● How much storage the name requiresProduction :D → integer, id D → real, id D → D1, id For declarations, an appropriate transformation scheme would be:

Production rule	Semantic action
D → integer, id	ENTER (id.PLACE, integer) D.ATTR = integer
D → real, id	ENTER (id.PLACE, real) D.ATTR = real
D → D1, id	ENTER (id.PLACE, D1.ATTR) D.ATTR = D1.ATTR

ENTER is used to enter the table of symbols and ATTR is used to trace the form of data. Q. 5) Define three address code with advantages ?Ans : Three Address CodeThree address statements are defined as a sentence that contains no more than three references (two for operands and one for outcomes). Three address codes are defined as a series of three address statements. The type x = y op z is a three address statement, where x, y, z would have an address (memory location). A statement may often contain fewer than three references, but it is still considered a statement of three addresses. Example – The code of the three addresses for the phrase : a + b * c + d :T 1 = b * cT 2 = a + T 1T 3 = T 2 + dT 1, T 2, T 3 are temporary variables . Advantages of three address code● For target code generation and optimization, the unravelling of complex arithmetic expressions and statements makes the three-address code ideal. ● Using names for the intermediate values determined by a programme makes it easy to rearrange the three-address code - unlike postfix notation. Q. 6) Write short notes on boolean expression ?Ans : Boolean ExpressionThere are two main uses of Boolean expressions. They are used in the estimation of logical values. They are often used when using if-then-else or while-do as a conditional expression. Consider the grammar E → E OR E E → E AND E E → NOT E E → (E) E → id relop id E → TRUE E → FALSE The relop is denoted by <, >, <, >.The AND and OR are still related. NOT has a higher precedent than AND and OR, ultimately.

Production rule	Semantic action
E → E1 OR E2	{E.place = newtemp(); Emit (E.place ':=' E1.place 'OR' E2.place) }
E → E1 + E2	{E.place = newtemp(); Emit (E.place ':=' E1.place 'AND' E2.place) }
E → NOT E1	{E.place = newtemp(); Emit (E.place ':=' 'NOT' E1.place) }
E → (E1)	{E.place = E1.place}
E → id relop id2	{E.place = newtemp(); Emit ('if' id1.place relop.op id2.place 'goto' nextstar + 3); EMIT (E.place ':=' '0') EMIT ('goto' nextstat + 2) EMIT (E.place ':=' '1') }
E → TRUE	{E.place := newtemp(); Emit (E.place ':=' '1') }
E → FALSE	{E.place := newtemp(); Emit (E.place ':=' '0') }

To generate the three address codes, the EMIT function is used and the newtemp () function is used to generate the temporary variables. The next state is found in the E → id relop id2 and provides the index of the next three address statements in the output sequence. Here is an example of how the three address code is created using the above translation scheme . p>q AND r<s OR u>r 100: if p>q goto 103 101: t1:=0 102: goto 104 103: t1:=1 104: if r>s goto 107 105: t2:=0 106: goto 108 107: t2:=1 108: if u>v goto 111 109: t3:=0 110: goto 112 111: t3:= 1 112: t4:= t1 AND t2 113: t5:= t4 OR t3 Q. 7) What is back patching ?
Ans : Back PatchingAll labels can not be recognised in a single pass in the code generation process (primarily, 3 Address Code), so we use a technique called Backpatching. Backpatching is the task of filling in unspecified label information during the code generation process using acceptable semantic behaviour. Three functions are used to implement the backpatching technique. The three functions performed in two passes to create code using backpatching are Makelist(), merge() and backpatch(). Three kinds of operations are carried out by Backpatching Algorithms

makelist(i) - Creates a new list that contains only an index in the quadruple array, and returns a pointer to the list that it has generated.

merge(p1,p2) - This function concatenates lists to which p1 and p2 are pointed, returning a pointer to the list of concatenated ones. This is used for assigning more than one address to the same true / false labels.

3. backpatch(p,i) - This role is used for the insertion of I as the target mark for each of the The statements in the list which p points to. All statements are attached using the data given by these feature labels. here ‘p’ is the pointer to any statement say p=> “if a<b goto ____”.Initially, we don’t know the label to fill just after goto.After backpatch(p,i)p=>“if a<b goto i”Q. 8) Write the difference between parse tree and syntax tree ?Ans : Differences between parse tree and syntax tree

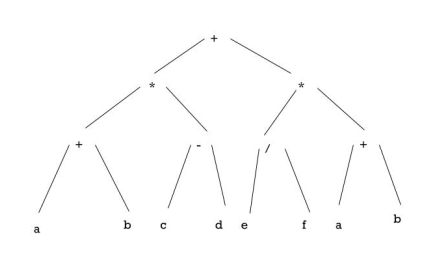
Parse Tree	Syntax Tree
A graphical representation of the substitution form in a derivation is the Parse tree.	The compact form of a parse tree is the syntax tree.
Any characteristic information from the real syntax is given by Parse trees.	Syntax trees do not have any of the actual syntax characteristics.
A terminal is defined by any leaf node.	An operand represents each leaf node.
Parse trees are relatively less dense than trees with syntax.	There are comparatively denser syntax trees than parse trees.
A grammar rule is defined by each interior node.	An operator is defined by any interior node.

Q. 9) For the following arithmetic expression, construct a syntax tree ?( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ))Ans : The Syntax tree is -

Q. 10) For the following arithmetic expression, construct a postfix notation?( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b )) Ans : We convert the arithmetic expression into Postfix Notation are -( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ) )ab+ * ( c – d ) + ( ( e / f ) * ( a + b ) )ab+ * cd- + ( ( e / f ) * ( a + b ) )ab+ * cd- + ( ef/ * ( a + b ) )ab+ * cd- + ( ef/ * ab+ )ab+ * cd- + ef/ab+*ab+cd-* + ef/ab+*ab+cd-*ef/ab+*+

Sign Up