Unit - 1

Concepts of Data structure, Array

Q1) Define Atomic data?

A1) Built-in Data types are data types for which a language provides built-in support.

Booleans, integers, characters, and floats are the four basic atomic data types.

Integers

The set of (positive and negative) integers that may be expressed in the fixed precision of a machine-sized word is known as the integer type int. The precise precision depends on the machine, but it will always be at least 32 bits. Standard integer functions are preset and employ infix notation (+, -, *, /, ==, >,, negate..) (see Appendix A for the precedence rules). Consider the following scenario:

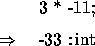
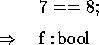
Overflow will return unpredictable results.

Boolean (true, false)

The boolean type bool has two possible values: t and f. Predefined logical operations include not, and, or, xor, nor, and nand. Infix notation is used for the operations and, or, xor, nor, and nand. Consider the following scenario:

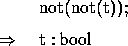
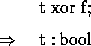
Floating (Decimal numbers)

Floating-point numbers are specified using the float type. Although the exact representation of these values varies by computer, NESL makes every effort to use 64-bit IEEE whenever available. Floats have a lot of the same functions as integers, but they also have a few more (eg. Round, truncate, sqrt, log,...). To distinguish floats from integers, they must be written with a decimal point in front of them.

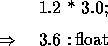
Between scalar types, there is no implicit coercion. To add 2 and 3.0, for example, one of them must be coerced: e.g.

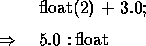
Character and Strings

The ASCII character set is represented by the character type char. All comparison procedures (e.g. ==, >=,...) can be utilized because the characters are in a set order. Putting a'in front of a character makes it easier to write. Consider the following scenario:

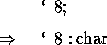
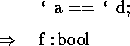
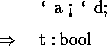
Space, newline, and tab are global variables that are associated with the proper characters.

Q2) What is data structure?

A2) A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.

Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.

Basic terminology

The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.

Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.

Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.

Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.

File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.

Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.

Q3) What do we need for data structure?

A3) Need of Data structure

As applications become more complicated and the amount of data collected grows, the following issues may arise:

●      Processor speed: High-speed processing is essential to manage vast amounts of data, however as data grows by the day to billions of files each entity, processors may be unable to handle that much data.

●      Data Search: Consider a store with a 106-item inventory. If our programme needs to search for a specific item, it must traverse all 106 items each time, which slows down the search process.

●      Multiple requests: If thousands of users are searching for data on a web server at the same time, there is a potential that a very large server will fail during the process.

Data structures are used to solve the difficulties listed above. Data is grouped into a data structure in such a way that not all things must be searched and essential data can be found quickly.

Q4) Write the advantages of data structure?

A4) Advantages of Data Structures

●      Efficiency: The efficiency of a programme is determined by the data structures used. Consider the following scenario: we have certain data and need to find a specific record. If we structure our data in an array, we will have to search element by element in such a scenario. As a result, employing an array may not be the most efficient solution in this case. There are more efficient data structures for searching, such as an ordered array, a binary search tree, or hash tables.

●      Reusability: Data structures are reusable, which means that after we've implemented one, we can use it somewhere else. Data structure implementations can be compiled into libraries that can be utilized by a variety of clients.

●      Abstraction: The ADT specifies the data structure, which provides a level of abstraction. The client software only interacts with the data structure through an interface, thus it isn't concerned with the implementation details.

Q5) Explain ADT with an example?

A5) The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user. The ADT is made of primitive data types, but operation logics are hidden.

Here we will see the stack ADT. These are a few operations or functions of the Stack ADT.

●      isFull(), This is used to check whether stack is full or not

●      isEmpty(), This is used to check whether stack is empty or not

●      push(x), This is used to push x into the stack

●      pop(), This is used to delete one element from top of the stack

●      peek(), This is used to get the top most element of the stack

●      size(), this function is used to get number of elements present into the stack

Example

#include<iostream>

#include<stack>

Using namespace std;

Main(){

   stack<int> stk;

   if(stk.empty()){

      cout << "Stack is empty" << endl;

   } else {

      cout << "Stack is not empty" << endl;

   }

   //insert elements into stack

   stk.push(10);

   stk.push(20);

   stk.push(30);

   stk.push(40);

   stk.push(50);

   cout << "Size of the stack: " << stk.size() << endl;

   //pop and display elements

   while(!stk.empty()){

      int item = stk.top(); // same as peek operation

      stk.pop();

      cout << item << " ";

   }

}

Output

Stack is empty

Size of the stack: 5

50 40 30 20 10

Q6) What is array operations?

A6) Array operations

The basic operations enabled by an array are listed below.

●      Traverse - prints each element of the array one by one.

●      Inserts - a new element at the specified index.

●      Deletes  - an element at the specified index.

●      Searches-  for an element based on the specified index or value.

●      Updates - an element at the specified index.

Traverse Operation

The traversal of an array's elements is performed with this operation.

Example

The following software walks an array and outputs its elements:

#include <iostream>

Using namespace std;

Int main()

{

Int i, size;

Int arr[]={53, 99, -11, 5, 102};    //declaring and initializing array

Size=sizeof(arr)/sizeof(arr[0]);

Cout << "The array elements are: ";

For(i=0;i<size;i++)

Cout << "\n" << "arr[" << i << "]= " << arr[i];

Return 0;

}

Output:

The array elements are:

Arr[0]= 53

Arr[1]= 99

Arr[2]= -11

Arr[3]= 5

Arr[4]= 102

Insertion Operation

One or more data elements are inserted into an array using the insert operation. A new element can be added to the beginning, end, or any provided index of the array, depending on the necessity.

We can see an actual implementation of the insertion action here, where we add data to the array's end.

Example

#include <iostream>

Using namespace std;

Int main()

{

Int i, size, x, pos;

Int arr[]={2, 4, 6, 8, 12};

Size=sizeof(arr)/sizeof(arr[0]);

Cout << "The array elements before insertion operation:\n";

For(i=0;i<size;i++)

Cout << "arr[" << i << "] = " << arr[i] << "\n";

Cout << "Enter the element to be insert: ";

Cin >> x;

Cout << "Enter the position where you want to insert the element: ";

Cin >> pos;

Size = size + 1;

Cout << "The array elements after insertion operation: ";

For(i=size-1;i>=pos-1;i--)

Arr[i+1]=arr[i];

Arr[pos-1]=x;

For(i=0;i<size;i++)

Cout << "\narr[" << i << "] = " << arr[i];

Return 0;

}

Output:

The array elements before insertion operation:

Arr[0] = 2

Arr[1] = 4

Arr[2] = 6

Arr[3] = 8

Arr[4] = 12

Enter the element to be insert: 786

Enter the position where you want to insert the element: 1

The array elements after insertion operation:

Arr[0] = 786

Arr[1] = 2

Arr[2] = 4

Arr[3] = 6

Arr[4] = 8

Arr[5] = 12

Deletion Operation

Deletion is the process of eliminating an existing element from an array and reorganizing all of its elements.

Algorithm

Consider the case where LA is a linear array with N items and K is a positive integer with the value N. The algorithm to delete an element available at the Kth position of LA is as follows.

Start

Set J = K

Repeat steps 4 and 5 while J < N

Set LA[J] = LA[J + 1]

Set J = J+1

Set N = N-1

Stop

Example:

#include <iostream>

Using namespace std;

Int main()

{

Int i, size, x, pos;

Int a[]={-1, 87, -68, 10, 8};

Size=sizeof(a)/sizeof(a[0]);

Cout << "The array elements before deletion operation:\n";

For(i=0;i<size;i++)

Cout << "a[" << i << "] = " << a[i] << "\n";

Cout << "Enter the position from where you wish to delete the element: ";

Cin >> pos;

Cout << "The array elements after deletion operation: ";

For(i=pos-1;i<size;i++)

a[i]=a[i+1];

Size = size - 1;

For(i=0;i<size;i++)

Cout << "\na[" << i << "] = " << a[i];

Return 0;

}

Output:

The array elements before deletion operation:

a[0] = -1

a[1] = 87

a[2] = -68

a[3] = 10

a[4] = 8

Enter the position from where you wish to delete the element: 2

The array elements after deletion operation:

a[0] = -1

a[1] = -68

a[2] = 10

a[3] = 8

Search Operation

A search for an array element can be done using its value or index.

Algorithm

Consider the case where LA is a linear array with N items and K is a positive integer with the value N. The algorithm for finding an element with the value ITEM using sequential search is as follows.

Start

Set J = 0

Repeat steps 4 and 5 while J < N

IF LA[J] is equal ITEM THEN GOTO STEP 6

Set J = J +1

PRINT J, ITEM

Stop

Example:

#include <iostream>

#define MAX 50

Using namespace std;

Int main()

{

Int i, n, x;

Int a[MAX];

Cout << "Enter the size of the array: ";

Cin >> n;

Cout << "Enter " << n << " elements:\n";

For(i=0;i<n;i++)

Cin >> a[i];

Cout << "Enter the element to search: ";

Cin >> x;

For(i=0;i<n;i++)

{

If(a[i]==x)

{cout << x << " found at " << i+1 << " position.";

Return 0;}

}

Cout << x << " not found";

Return 0;

}

Output:

Enter the size of the array: 5

Enter 5 elements:

11

22

33

-512

99

Enter the element to search: -512

-512 found at 4 position.

Update Operation

The update action updates an existing element in the array at a specified index.

Algorithm

Consider the case where LA is a linear array with N items and K is a positive integer with the value N. The algorithm to update an element available at the Kth location of LA is as follows.

1. Start

2. Set LA[K-1] = ITEM

3. Stop

Example:

#include <iostream>

Using namespace std;

Int main()

{

Int i, size, x, pos;

Int a[]={1, 3, 5, 7, 9};

Size=sizeof(a)/sizeof(a[0]);

Cout <<  "The array elements before update operation are:" ;

For(i=0;i<size;i++)

Cout << "\n" << "a[" << i << "]= " << a[i];

Cout << "\nThe position where you wish to update the element: ";

Cin >> pos;

Cout << "The new element: ";

Cin >> x;

a[pos-1]=x;

Cout << "The array elements after update operation are:";

For(i=0;i<size;i++)

Cout << "\n" << "a[" << i << "]= " << a[i];

}

Output:

The array elements before update operation are:

a[0]= 1

a[1]= 3

a[2]= 5

a[3]= 7

a[4]= 9

The position where you wish to update the element: 3

The new element: -10

The array elements after update operation are:

a[0]= 1

a[1]= 3

a[2]= -10

a[3]= 7

a[4]= 9

Q7) Write the applications of Array?

A7) Application of Array

●      Vectors and lists, which are fundamental parts of the C++ STL, are implemented using arrays.

●      Stacks and queues are also implemented using arrays.

●      Whenever possible, trees employ array implementation since arrays are easier to manage than pointers. Tress is then utilized to construct a variety of additional data structures.

●      Arrays are used to implement matrices, which are an important aspect of every computer language's mathematics library.

●      The graph's adjacency list is implemented using vectors, which are then implemented using arrays.

●      Binary search trees and balanced binary trees, which can be built using arrays, are used in data structures such as a heap, map, and set.

●      Multiple variables with the same name are stored in arrays.

●      Arrays are used to develop CPU scheduling algorithms.

●      Arrays are at the heart of all sorting algorithms.

Q8) Define a multidimensional array?

A8) Multidimensional Arrays

a 2D array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns.

However, 2D arrays are created to implement a relational database look alike data structure. It provides ease of holding bulk data at once which can be passed to any number of functions wherever required.

How to declare 2D Array

The syntax of declaring a two dimensional array is very much similar to that of a one dimensional array, given as follows.

Int arr[max_rows][max_columns];  

However, It produces the data structure which looks like the following.

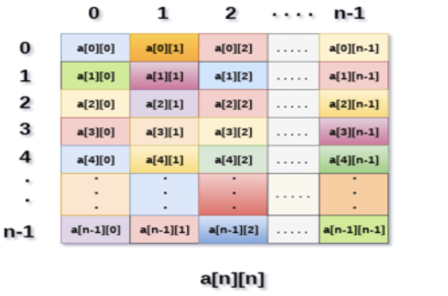
Fig 1:  Example

Above image shows the two dimensional array, the elements are organized in the form of rows and columns. First element of the first row is represented by a[0][0] where the number shown in the first index is the number of that row while the number shown in the second index is the number of the column.

How do we access data in a 2D array

Due to the fact that the elements of 2D arrays can be random accessed. Similar to one dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells. There are two indices attached to a particular cell, one is its row number while the other is its column number.

However, we can store the value stored in any particular cell of a 2D array to some variable x by using the following syntax.

Int x = a[i][j];  

Where i and j is the row and column number of the cell respectively.

We can assign each cell of a 2D array to 0 by using the following code:

1. For ( int i=0; i<n ;i++) 
2. { 
3.     for (int j=0; j<n; j++)  
4.     { 
5.         a[i][j] = 0;  
6.     } 
7. } 

Initializing 2D Arrays

We know that, when we declare and initialize a one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array.

The syntax to declare and initialize the 2D array is given as follows.

Int arr[2][2] = {0,1,2,3};  

The number of elements that can be present in a 2D array will always be equal to (number of rows * number of columns).

Q9) Write any example of an array?

A9)

#include<iostream>

Using namespace std;

Main( )

{ 

      int  s[2][2];

      int  i, j;

      cout<<"\n2D Array Input:\n";

  for(i=0;i<2;i++)

  {

  for(j=0;j<2;j++)

  {

  cout<<"\ns["<<i<<"]["<<j<<"]=  ";

  cin>>s[i][j];

}

  }

  cout<<"\nThe 2-D Array is:\n";

      for(i=0;i<2;i++)

  {

  for(j=0;j<2;j++)

  {

  cout<<"\t"<<s[i][j];

}

Cout<<endl;

  }

Q10) How to represent an array?

A10) Arrays can be declared in a variety of ways depending on the language.

Arrays can be declared in a variety of ways depending on the language. Consider the C array declaration as an example.

The following are the key points to consider, as shown in the diagram above.

●      The index begins with a zero.

●      The length of the array is 10, which indicates it can hold ten elements.

●      The index of each element can be used to access it. For example, an element at index 6 can be retrieved as 9.

Q11) Write about update operation?

A11) Update Operation

The update action updates an existing element in the array at a specified index.

Algorithm

Consider the case where LA is a linear array with N items and K is a positive integer with the value N. The algorithm to update an element available at the Kth location of LA is as follows.

1. Start

2. Set LA[K-1] = ITEM

3. Stop

Example:

#include <iostream>

Using namespace std;

Int main()

{

Int i, size, x, pos;

Int a[]={1, 3, 5, 7, 9};

Size=sizeof(a)/sizeof(a[0]);

Cout <<  "The array elements before update operation are:" ;

For(i=0;i<size;i++)

Cout << "\n" << "a[" << i << "]= " << a[i];

Cout << "\nThe position where you wish to update the element: ";

Cin >> pos;

Cout << "The new element: ";

Cin >> x;

a[pos-1]=x;

Cout << "The array elements after update operation are:";

For(i=0;i<size;i++)

Cout << "\n" << "a[" << i << "]= " << a[i];

}

Output:

The array elements before update operation are:

a[0]= 1

a[1]= 3

a[2]= 5

a[3]= 7

a[4]= 9

The position where you wish to update the element: 3

The new element: -10

The array elements after update operation are:

a[0]= 1

a[1]= 3

a[2]= -10

a[3]= 7

a[4]= 9

Q12) Explain deletion operation of array?

A12) Deletion Operation

Deletion is the process of eliminating an existing element from an array and reorganizing all of its elements.

Algorithm

Consider the case where LA is a linear array with N items and K is a positive integer with the value N. The algorithm to delete an element available at the Kth position of LA is as follows.

Start

Set J = K

Repeat steps 4 and 5 while J < N

Set LA[J] = LA[J + 1]

Set J = J+1

Set N = N-1

Stop

Example:

#include <iostream>

Using namespace std;

Int main()

{

Int i, size, x, pos;

Int a[]={-1, 87, -68, 10, 8};

Size=sizeof(a)/sizeof(a[0]);

Cout << "The array elements before deletion operation:\n";

For(i=0;i<size;i++)

Cout << "a[" << i << "] = " << a[i] << "\n";

Cout << "Enter the position from where you wish to delete the element: ";

Cin >> pos;

Cout << "The array elements after deletion operation: ";

For(i=pos-1;i<size;i++)

a[i]=a[i+1];

Size = size - 1;

For(i=0;i<size;i++)

Cout << "\na[" << i << "] = " << a[i];

Return 0;

}

Q13) Write the difference between single array or two dimension array?

A13) Difference between one dimensional and two dimensional array