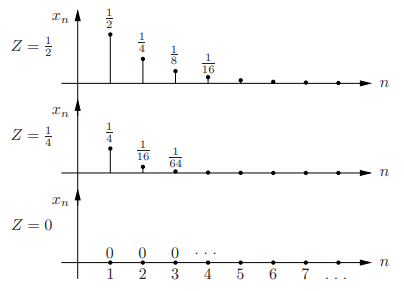
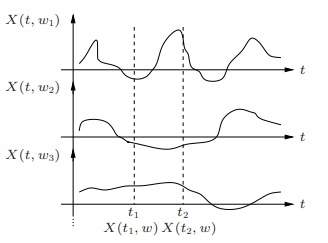
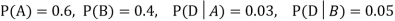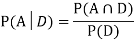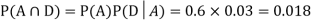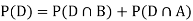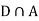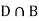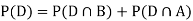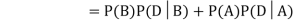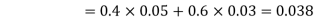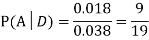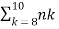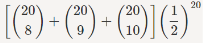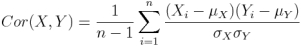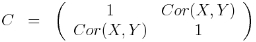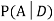undefined | unit 1 probability theory random variable process

Back to Study material

UNIT-1Probability Theory, Random Variable & Process Q1) Factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.A1) We consider the following events: A: Selected item comes from A. B: Selected item comes from B. D: Selected item is defective.We are looking for

. We know:

Now,

So we need

Since, D is the union of the mutually exclusive events and (the entire sample space is the union of the mutually exclusive events A and B)

Q2) In a communication system each data packet consists of 1000 bits. Due to the noise, each bit may be received in error with probability 0.1. It is assumed bit errors occur independently. Find the probability that there are more than 120 errors in a certain data packet.A2) Let us define Xi as the indicator random variable for the ith bit in the packet. That is, Xi=1 if the ith bit is received in error, and Xi=0 otherwise. Then the Xi's are i.i.d. and Xi∼Bernoulli(p=0.1).

If Y is the total number of bit errors in the packet, we have

Y=X1+X2+...+Xn.

Since Xi∼Bernoulli(p=0.1), we have

EXi=μ=p=0.1,Var(Xi)=σ2=p(1−p)=0.09

Using the CLT, we have

P(Y>120)=P(Y−nμ/ √nσ>120−nμ/√nσ)

=P(Y−nμ/√nσ>120−100/ √90)

≈1−Φ(20/√90)=0.0175

Continuity Correction:

Let us assume that Y∼Binomial(n=20,p=12), and suppose that we are interested in P(8≤Y≤10). We know that a Binomial(n=20,p=12) can be written as the sum of n i.i.d. Bernoulli(p) random variables:

Y=X1+X2+...+Xn.

Since Xi∼Bernoulli(p=12), we have

EXi=μ=p=12,Var(Xi)=σ2=p(1−p)=14.

Thus, we may want to apply the CLT to write

P(8≤Y≤10)=P(8−nμ/√nσ<Y−nμ/√nσ<10−nμ/ √nσ)

=P(8−10/√5 <Y−nμ/ √nσ<10−10/ √5)≈Φ(0)−Φ(−2/√5)=0.3145

Since, here, n=20 is relatively small, we can actually find P(8≤Y≤10) accurately. We have

P(8≤Y≤10)=pk(1−p)n−k

=0.4565

We notice that our approximation is not so good. Part of the error is due to the fact that Y is a discrete random variable and we are using a continuous distribution to find P(8≤Y≤10). Here is a trick to get a better approximation, called continuity correction. Since Y can only take integer values, we can write

P(8≤Y≤10)

=P(7.5<Y<10.5)

=P(7.5−nμ/√nσ<Y−nμ/√nσ<10.5−nμ/√nσ)

=P(7.5−10/√5 <Y−nμ/√nσ<10.5−10/√5)

≈Φ(0.5/√5)−Φ(−2.5/√5)

=0.4567

As we see, using continuity correction, our approximation improved significantly. The continuity correction is particularly useful when we would like to find P(y1≤Y≤y2), where Y is binomial and y1 and y2 are close to each other.

If Z ∼ U[0, 1], and define the discrete time process Xn = Z n for n ≥ 1

• Sample paths:

Fig.: Sample paths First-order pdf of the process: For each n, Xn = Z n is a r.v.; the sequence of pdfs of Xn is called the first-order pdf of the process

Fig.: First-order pdf of the process Since Xn is a differentiable function of the continuous r.v. Z, we can find its pdf as ffXn (x) = 1/( nx(n−1)/n) = 1/n x(1/n)−1) , 0 ≤ x ≤ 1 Q3) Write the classification of random process.A3) Random processes are classified according to the type of the index variable and classification of the random variables obtained from samples of the random process. The major classification is given below:

Q4) Define PSD.A4) A Power Spectral Density (PSD) is the measure of signal's power content versus frequency. A PSD is typically used to characterize broadband random signals. The amplitude of the PSD is normalized by the spectral resolution employed to digitize the signal.For vibration data, a PSD has amplitude units of g2/Hz. While this unit may not seem intuitive at first, it helps ensure that random data can be overlaid and compared independently of the spectral resolution used to measure the data.

The average power {\displaystyle P}P of a signal {\displaystyle x(t)}x(t) over all time is therefore given by the following time average:

Q5) Let X(t) be a zero-mean WSS process with RX(τ)=e−|τ|. X(t) is input to an LTI system with|H(f)|=√ (1+4π2f2) |f|<2 = 0 otherwise Let Y(t) be the output.

Find μY(t)=E[Y(t)]

Find RY(τ)

Find E[Y(t)2]

A5)

Note that since X(t) is WSS, X(t) and Y(t) are jointly WSS, and therefore Y(t) is WSS.
1. To find μY(t), we can write

μY=μX H(0) =0*1= 0

b. To find RY(τ), we first find SY(f)

SY(f)=SX(f)|H(f)|2

From Fourier transform tables, we can see that

SX(f)=F{e−|τ|}=2/(1+(2πf)2)

Then, we can find SY(f) as

SY(f)=SX(f)|H(f)|2

=2 |f|<2

= 0 otherwise

We can now find RY(τ) by taking the inverse Fourier transform of SY(f)

RY(τ)=8 sinc(4τ),

where

sinc(f)=sin(πf)/πf

c. We have

E[Y(t)2]=RY(0)=8.

Q6) What are the two Ways to View a Random Process. A6) A random process can be viewed as a function X(t, ω) of two variables, time t ∈ T and the outcome of the underlying random experiment ω ∈ Ω ◦ For fixed t, X(t, ω) is a random variable over Ω ◦ For fixed ω, X(t, ω) is a deterministic function of t, called a sample function

Fig.: Random Process A random process is said to be discrete time if T is a countably infinite set, e.g., ◦ N = {0, 1, 2, . . .} ◦ Z = {. . . , −2, −1, 0, +1, +2, . . .} • In this case the process is denoted by Xn, for n ∈ N , a countably infinite set, and is simply an infinite sequence of random variables • A sample function for a discrete time process is called a sample sequence or sample path • A discrete-time process can comprise discrete, continuous, or mixed r.v.s Q7) How to Apply The Central Limit Theorem (CLT)A7) Here are the steps that we need in order to apply the CLT:

1.Write the random variable of interest, Y, as the sum of n i.i.d. random variable Xi's:

Y=X1+X2+...+Xn.

2.Find EY and Var(Y) by noting that

EY=nμ,Var(Y)=nσ2,

where μ=EXi and σ2=Var(Xi).

3.According to the CLT, conclude that

Y−EY/ √Var(Y)=Y−nμ/ √nσ is approximately standard normal; thus, to find P(y1≤Y≤y2), we can write

P(y1≤Y≤y2)=P(y1−nμ/√nσ≤Y−nμ/√nσ≤y2−nμ/√nσ)

≈Φ(y2−nμ/ √nσ)−Φ(y1−nμ/√nσ).

Q8) State and explain central limit theorem.A8) The central limit theorem (CLT) is one of the most important results in probability theory.It states that, under certain conditions, the sum of a large number of random variables is approximately normal.

Here, we state a version of the CLT that applies to i.i.d. random variables. Suppose that X1, X2 , ... , Xn are i.i.d. random variables with expected values EXi=μ<∞ and variance Var(Xi)=σ2<∞. Then the sample mean X¯¯=X1+X2+...+Xnn has mean EX¯=μ and variance Var(X¯)=σ2n.

Where,
μ = Population mean

σ = Population standard deviation

μx¯= Sample mean

σx¯ = Sample standard deviation

n = Sample size

Q9) Define correlation.A9) The covariance has units (units of X times units of Y), and thus it can be difficult to assess how strongly related two quantities are. The correlation coefficient is a dimensionless quantity that helps to assess this.

The correlation coefficient between X and Y normalizes the covariance such that the resulting statistic lies between -1 and 1. The Pearson correlation coefficient

is eqn8836e

The correlation matrix for X and Y is

eqn8836g

Sign Up