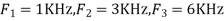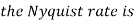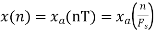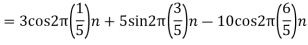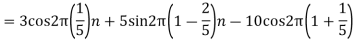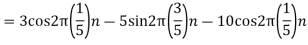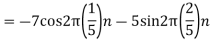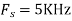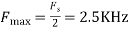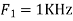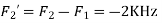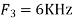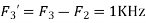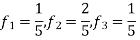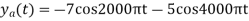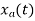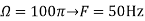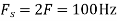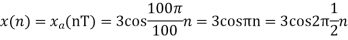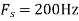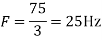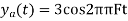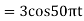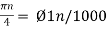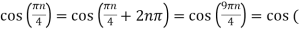We know, X[n] =x(nT) = cos(200πnT) = cos(2πn/3) , where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
|
 S2)The frequency in the analog signal
S2)The frequency in the analog signal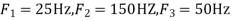 The largest frequency is
The largest frequency is The Nyquist rate is
The Nyquist rate is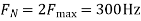 Q3) The analog signal
Q3) The analog signal
 . What is discrete time signal obtained after sampling?
. What is discrete time signal obtained after sampling?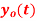 we can reconstruct from the samples if we use ideal interpolation?
we can reconstruct from the samples if we use ideal interpolation?
2. For
For Hence
So that normalizing frequencies are
The analog signal that we can recover is
Which is different than the original signal
|

 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling?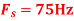 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling? a. The minimum sampling rate is
And the discrete time signal is
b. if
c. If Fs=75Hz , the discrete time signal is
d. For the sampling rate
So, the analog sinusoidal signal is
|
S5) Taking T= 1/1000s cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000) Ø1 is easily computed as Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
Ø2 = 2250π
|
|
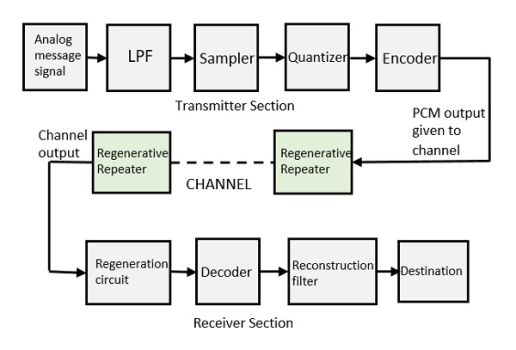
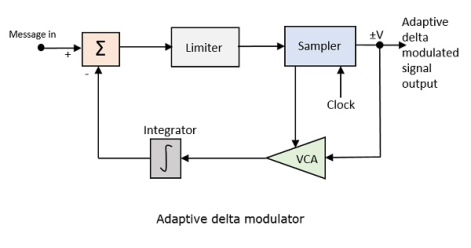
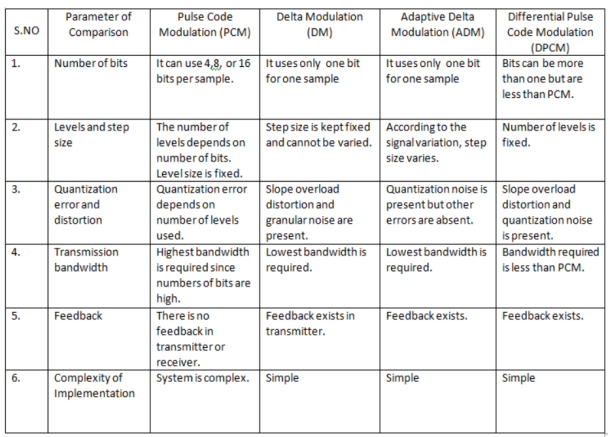
Because it's necessary to predict sample value DPCM is form of predictive coding.DPCM compression depends on the prediction technique, well-conducted prediction techniques lead to good compression rates, in other cases DPCM could mean expansion comparing to regular PCM encoding.
|
|