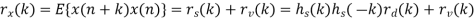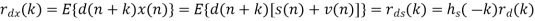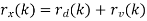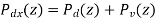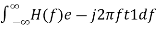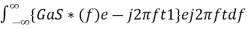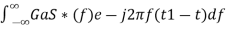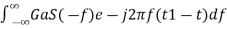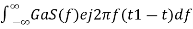| unit 3 digital signalling formats

Back to Study material

UNIT-3Digital Signalling Formats Q1) What is a base band signal receiver? Draw and explain.A1) The elements which form a digital communication system is given by

Digital Communication

Fig.: Digital receivers Following are the sections of the digital communication system.

SourceThe source can be an analog signal. Example: A Sound signalInput TransducerThis is a transducer which takes a physical input and converts it to an electrical signal (Example: microphone). This block also consists of an analog to digital converter where a digital signal is needed for further processes.A digital signal is generally represented by a binary sequence.Source EncoderThe source encoder compresses the data into minimum number of bits. This process helps in effective utilization of the bandwidth. It removes the redundant bits unnecessary excess bits i.e. zeroes unnecessary excess bits, i.e. zeroes. Channel EncoderThe channel encoder, does the coding for error correction. During the transmission of the signal, due to the noise in the channel, the signal may get altered and hence to avoid this, the channel encoder adds some redundant bits to the transmitted data. These are the error correcting bits.Digital ModulatorThe signal to be transmitted is modulated here by a carrier. The signal is also converted to analog from the digital sequence, in order to make it travel through the channel or medium.ChannelThe channel or a medium, allows the analog signal to transmit from the transmitter end to the receiver end.Digital DemodulatorThis is the first step at the receiver end. The received signal is demodulated as well as converted again from analog to digital. The signal gets reconstructed here.Channel DecoderThe channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits. This addition of bits helps in the complete recovery of the original signal.Source DecoderThe resultant signal is once again digitized by sampling and quantizing so that the pure digital output is obtained without the loss of information. The source decoder recreates the source output.Output TransducerThis is the last block which converts the signal into the original physical form, which was at the input of the transmitter. It converts the electrical signal into physical output (Example: loud speaker).Output SignalThis is the output which is produced after the whole process. Example − The sound signal received. Q2) Write a note on integrate and dump filter.A2)

The Integrate and Dump Filter (IDF) is used as a matched filter for the detection of signals in additive white Gaussian noise.

The performance of the digital integrate and dump filter is evaluated.

The case considered is when symbol times are known and the sampling clock is free running at a constant rate, i.e., the sampling clock is not phase locked to the symbol clock.

Degradations in the output signal to noise ratio of the digital implementation due to sampling rate, sampling offset, and finite bandwidth, resulting from the anti-aliasing low pass prefilter, are computed and compared with those of the analog counterpart.

It is shown that the digital IDF performs within 0.6 dB of the ideal analog IDF whenever the prefilter bandwidth exceeds four times the symbol rate and when sampling is performed at the Nyquist rate.

The loss can be reduced to 0.3 dB by doubling the sampling rate, where 0.2 dB loss results from finite bandwidth and 0.1 dB results from the digital IDF

Fig.: Integrate and dump filter Q3) Explain Optimum filterA3) An optimum filter is such a filter used for acquiring a best estimate of desired signal from noisy measurement. It is different from the classic filters. These filters are optimum because they are designed based on optimization theory to minimize the mean square error between a processed signal and a desired signal, or equivalently provides the best estimation of a desired signal from a measured noisy signal.It is pervasive that when we measure a (desired) signal d(n), noise v(n) interferes with the signal so that a measured signal becomes a noisy signal x(n) x(n)=d(n)+v(n) It is also very common that a signal d(n) is distorted in its measurement (e.g., an electromagnetic signal distorts as it propagates over a radio channel). Assuming that the system causing distortion is characterized by an impulse response of h (n) s , the measurement of d(n) can be expressed by the sum of distorted signal s(n) and noise

v(n) x(n)=s(n)+v(n)= h (n)∗ s d(n)+v(n)

where s(n)= h (n)∗ s d(n).

If both d(n) and v(n) are assumed to be wide-sense stationary (WSS) random processes, then x(n) is also a WSS process. The signals that we discuss in this chapter will be WSS if they are not specially specified. If signal d(n) and measurement noise v(n) are assumed to be uncorrelated (this is true in many practical cases), then r (k) = r (k) = 0.

In this case, the noisy signal,

x(n)= h (n)∗ s d(n)+v(n),

the relation of r (k) x with r (k ) d and r (k) v (the autocorrelations of x(n), d(n) and v(n), respectively) as follows,

For the noisy signal of the form x(n)= d(n)+v(n), a special case of where h (n) s =δ (n) and no distortion happens to d(n) in its measurement, we have

Optimum filtering is to acquire the best linear estimate of a desired signal from a measurement. The main issues in optimal filtering contain• filtering that deals with recovering a desired signal d(n) from a noisy signal (or measurement) x(n); • prediction that is concerned with predicting a signal d(n+m) for m>0 from observation x(n); • smoothing that is an a posteriori form of estimation, i.e., estimating d(n+m) for m

Fig.: Optimum filterQ4) Explain Matched filter in detail.A4) If a filter produces an output in such a way that it maximizes the ratio of output peak power to mean noise power in its frequency response, then that filter is called Matched filter.

Fig.: Matched filter

Frequency Response Function of Matched FilterThe frequency response of the Matched filter will be proportional to the complex conjugate of the input signal’s spectrum. Mathematically, we can write the expression for frequency response function, H(f) of the Matched filter as −

H(f)=GaS∗(f)e−j2πft1 ………..1

Where,

Ga is the maximum gain of the Matched filter

S(f) is the Fourier transform of the input signal, s(t)

S∗(f) is the complex conjugate of S(f)

t1 is the time instant at which the signal observed to be maximum

In general, the value of Ga is considered as one. We will get the following equation by substituting Ga=1in Equation 1.

H(f)=S∗(f)e−j2πft1 ……..2

The frequency response function, H(f) of the Matched filter is having the magnitude of S∗(f)and phase angle of e−j2πft1, which varies uniformly with frequency.

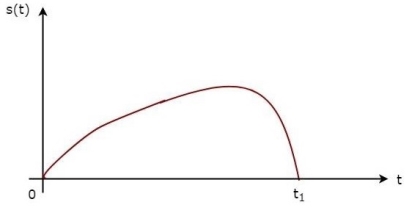
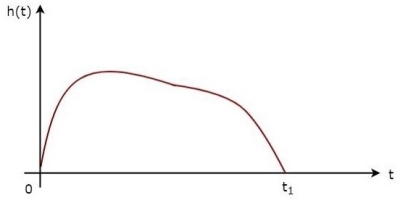
Impulse Response of Matched Filter

In time domain, we will get the output, h(t) of Matched filter receiver by applying the inverse Fourier transform of the frequency response function, H(f).

h(t)= ….….3

Substitute, Equation 1 in Equation 3.

h(t)=

⇒h(t)= ………4

We know the following relation.

S∗(f)=S(−f) ……..5

Substitute, Equation 5 in Equation 4.

h(t)=

⇒h(t)=

⇒h(t)=Gas(t1−t)

In general, the value of Ga is considered as one. We will get the following equation by substituting Ga=1.

h(t)=s(t1−t)

The above equation proves that the impulse response of Matched filter is the mirror image of the received signal about a time instant t1. The following figures illustrate this concept.

Impulse Response

Matched Filter

Fig.: Impulse response of Matched filterThe received signal, s(t) and the impulse response, h(t) of the matched filter corresponding to the signal, s(t) are shown in the above figures. Q5) What is Inter symbol interference? Write its causes.A5) This is a form of distortion of a signal, in which one or more symbols interfere with subsequent signals, causing noise or delivering a poor output.Causes of ISIThe main causes of ISI are −

Multi-path Propagation

Non-linear frequency in channels

The ISI is unwanted and should be completely eliminated to get a clean output. The causes of ISI should also be resolved in order to lessen its effect.To view ISI in a mathematical form present in the receiver output, we can consider the receiver output.

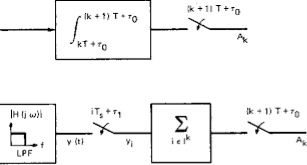
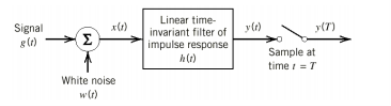
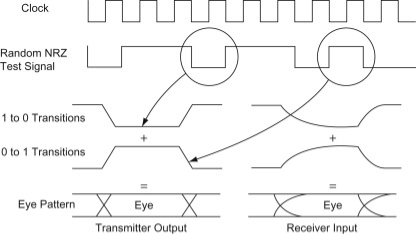
The receiving filter output y(t)y(t) is sampled at time ti=iTb (with i taking on integer values), yielding –

y(ti)= μ∑akp(iTb−kTb)

= μai+μ∑akp(iTb−kTb)

In the above equation, the first term μai is produced by the ith transmitted bit.The second term represents the residual effect of all other transmitted bits on the decoding of the ith bit. This residual effect is called as Inter Symbol Interference.In the absence of ISI, the output will be −y(ti)=μaiThis equation shows that the ith bit transmitted is correctly reproduced. However, the presence of ISI introduces bit errors and distortions in the output.While designing the transmitter or a receiver, it is important that you minimize the effects of ISI, so as to receive the output with the least possible error rate. Q6) Explain Eye diagram in short. A6) An eye diagram or eye pattern is simply a graphical display of a serial data signal with respect to time that shows a pattern that resembles an eye. The signal at the receiving end of the serial link is connected to an oscilloscope and the sweep rate is set so that one- or two-bit time periods (unit intervals or UI) are displayed. This causes bit periods to overlap and the eye pattern to form around the upper and lower signal levels and the rise and fall times. The eye pattern readily shows the rise and fall time lengthening and rounding as well as the horizontal jitter variation.

Fig. : eye diagram Q7) Explain Scrambler and its types.A7)Scrambler is a device that transposes or inverts signals or otherwise encodes a message at the sender's side to make the message unintelligible at a receiver not equipped with an appropriately set descrambling device. Whereas encryption usually refers to operations carried out in the digital domain, scrambling usually refers to operations carried out in the analog domain. Scrambling is accomplished by the addition of components to the original signal or the changing of some important component of the original signal in order to make extraction of the original signal difficult. Examples of the latter might include removing or changing vertical or horizontal sync pulses in television signals; televisions will not be able to display a picture from such a signal. Some modern scramblers are actually encryption devices, the name remaining due to the similarities in use, as opposed to internal operation. Types:

Additive (synchronous) scramblers

Additive scramblers (they are also referred to as synchronous) transform the input data stream by applying a pseudo-random binary sequence (PRBS) (by modulo-two addition). Sometimes a pre-calculated PRBS stored in the read-only memory is used, but more often it is generated by a linear-feedback shift register (LFSR).

Multiplicative (self-synchronizing) scramblers

Multiplicative scramblers (also known as feed-through) are called so because they perform a multiplication of the input signal by the scrambler's transfer function in Z-space. They are discrete linear time-invariant systems. A multiplicative scrambler is recursive, and a multiplicative descrambler is non-recursive. Unlike additive scramblers, multiplicative scramblers do not need the frame synchronization, that is why they are also called self-synchronizing.

Q8) Explain Frame and time synchronization.A8)Frame synchronizationIn modern computer networks data is not transferred as a simple stream of bits or bytes but in terms of frames or packets. This enables amongst other things packet based routing, error correction and the sharing of one physical medium between multiple clients. As the medium usually is a serial link and does not have a concept of frames or separated data units the sender and receiver have to recognize frame borders in the data stream on the medium. This process is called Frame Synchronization. Time gap synchronization The most obvious method for synchronization is leaving a time gap between frames. This is of course only possible if an idle state of the transfer medium is recognizable and distinguishable from for example a long row of zeros. If the bits are encoded using return to zero signalling time gaps cannot be used. While this is simple and easy to implement it has disadvantages too. To make sure each of the communication partners recognizes the time gap as such it has to be long enough compared to the length of one information cell in asynchronous data transfers. This brings a performance penalty. Time gap synchronization is usually used in combination with another method of frame synchronization like packet length indication because it might fail if line noise is encountered and by that needs a backup technique.

Sign Up