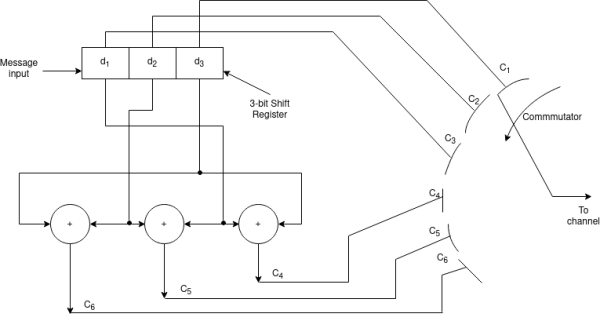
Code name | Msg Vector | Code Vector For (6,3) liner block code |
| d 1 d 2 d3 | d 1 d 2 d 3 d 1+d 3 d2 + d3 d1 + d2 |
Ca | 0 0 0 | 0 0 0 0 0 0 |
Cb | 0 0 1 | 0 0 1 1 1 0 |
Cc | 0 1 0 | 0 1 0 0 1 1 |
Cd | 0 1 1 | 0 1 1 1 0 1 |
Ce | 1 0 0 | 1 0 0 1 0 1 |
Cf | 1 0 1 | 1 0 1 0 1 1 |
Cg | 1 1 0 | 1 1 0 1 1 0 |
Ch | 1 1 1 | 1 1 1 0 0 0 |
|
1 | 0 | 1 |
0 | 1 | 1 |
1 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
1 | 0 | 1 |
0 | 1 | 1 |
1 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
|
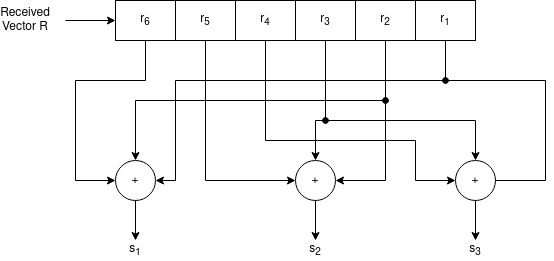
P = 1 0 1 0 1 1 1 1 0
P T = 1 0 1 0 1 1 1 1 0 Parity check matrix [H] = [P T | I n-k] = [ PT | I3 ] 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1
H T = 1 0 1 0 1 1 1 1 0 1 0 0 0 1 0 0 0 1 S = [s1 s2 s3] = R HT= [ 11 00 10] 1 0 1 0 1 1 1 1 0 1 0 0 0 1 0 0 0 1 [S]= [100] since s≠0 it represents error. Since [100] present in the 4th row of HT . So the error vector [E] = [0 0 0 1 0 0 ] the the corrected vector is given by C = R + E = [11 00 10][000100] C = [110110] which is the valid code
|
|
|
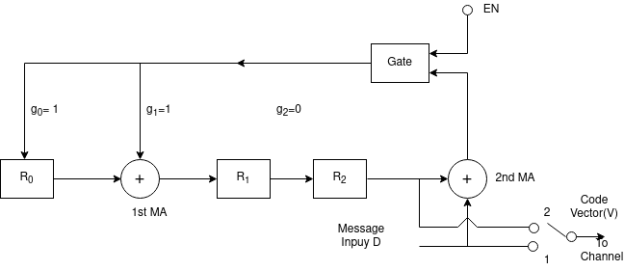
Number of shifts | Input Z(x) | Shift register contents | Comments |
Initialization gate1-oFF and gate-2 ON |
| 000 | Shift register contents are cleared |
1 | 1 | 100 |
|
2 | 0 | 010 |
|
3 | 1 | 101 |
|
4 | 0 | 100 |
|
5 | 1 | 110 |
|
6 | 1 | 111 |
|
7 | 1 | 001 | Indicates error |
8 | 0 | 110 |
|
9 | 0 | 011 |
|
10 | 0 | 111 |
|
11 | 0 | 101 |
|
12 | 0 | 100 | Endof shifting operation |
|
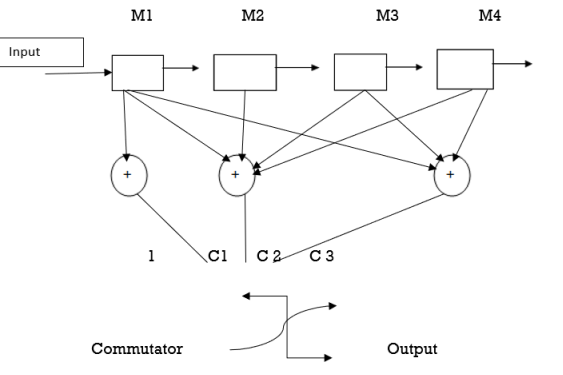
 s2
s2  s3
s3  s4c3 = s1
s4c3 = s1  s3
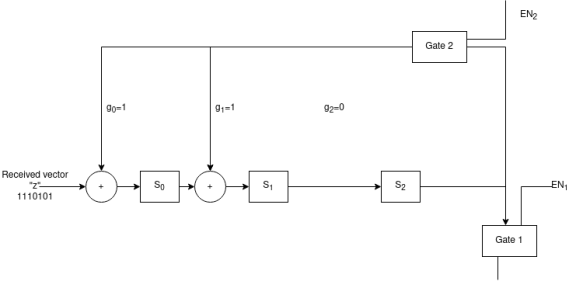
s3  s4We assume that initially the shift register is clear. During the first shift M1 = 1 M2 = M3=M4 = 0C1 = s1 = 1C2 = = s1
s4We assume that initially the shift register is clear. During the first shift M1 = 1 M2 = M3=M4 = 0C1 = s1 = 1C2 = = s1  s2
s2  s3
s3  s4 = 1
s4 = 1 0
0 0
0 0 =1C3 = s1
0 =1C3 = s1  s3
s3  s4= 1
s4= 1  0
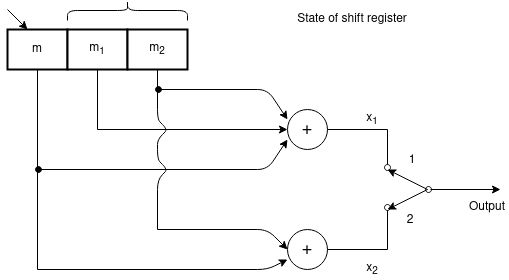
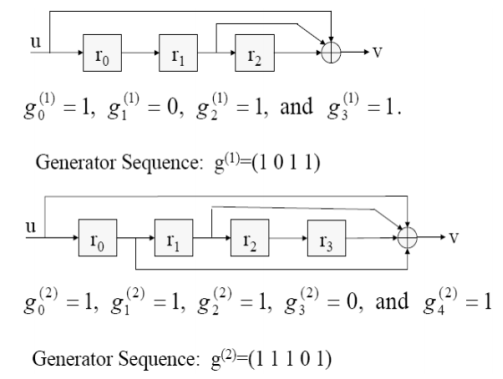
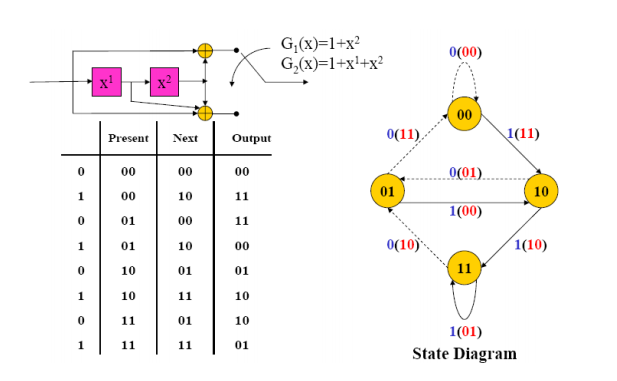
0 0 = 1The coded output for tbis message bit is 111C = 111 010 100 110 001 000 011 000 000 Q8) Assume a (2,1) convolutional encoder with constraint length 6. Draw the tree diagram , state diagram . Design the block code for a message block of size eight that can correct single errors . A8) Here :n = 2 and k =1 and K = 6 ( constraint length)M = K/n = 6/2 = 3 since constraint length k = n * M
0 = 1The coded output for tbis message bit is 111C = 111 010 100 110 001 000 011 000 000 Q8) Assume a (2,1) convolutional encoder with constraint length 6. Draw the tree diagram , state diagram . Design the block code for a message block of size eight that can correct single errors . A8) Here :n = 2 and k =1 and K = 6 ( constraint length)M = K/n = 6/2 = 3 since constraint length k = n * M
|
|
|
|
|
|
|