undefined | unit 3 op amp configuration and frequency response

LIC

UNIT - 3Op-Amp Configuration and Frequency Response Q1) A 200mV peak to peak sine waveform voltage is applied to Op-amp inverting amplifier with Rf/R1 = 10.?A1) Peak to peak input voltage 2Vm = 200 mV Vm = 100 mVVi= Vm sin wt = 100 sin wt mV Vo = -Rf/R1 x vi = -10 x 100 sinwt mV = -1000 sin wt mV Q2) Design a non-inverting amplifier using Op-amp with a closed loop voltage gain of 10?A2) Af = 1 + Rf/R1 =10 Rf/R1 = 9Rf = 9 R1 If R1 = 1KRf = 9K ΩQ3) In an op-amp inverting amplifier R1 = 1K Ω and Rf = 100KΩ. The DC supply voltage of the op-amp is ± 15V. Calculate the output voltage if input voltage is 1V?A3)R1 = 1KΩ Rf = 100KΩV+ = 15V and V-=-15V. vi = 1VAf = -Rf/R1 = -100K/1K = -100Af = vo/vi Vo = Af vi = -100 x 1V = -100VThe output voltage cannot exceed the DC power supply voltage. Since vo is negative and large it is limited to V-Vo ≈ V- = -15V Q4) Compare inverting, non-inverting and differential amplifier?A4)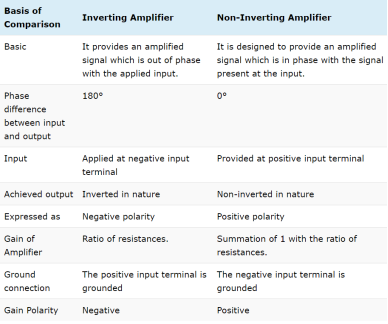

Q5) Explain voltage series amplifier?A5) In the voltage series feedback circuit, a fraction of the output voltage is applied in series with the input voltage through the feedback circuit. This is also known as shunt-driven series-fed feedback, i.e., a parallel-series circuit.The following figure shows the block diagram of voltage series feedback, by which it is evident that the feedback circuit is placed in shunt with the output but in series with the input.

Fig 4 Voltage Series Feedback As the feedback circuit is connected in shunt with the output, the output impedance is decreased and due to the series connection with the input, the input impedance is increased. Q6) Explain voltage shunt feedback amplifier?A6) In the voltage shunt feedback circuit, a fraction of the output voltage is applied in parallel with the input voltage through the feedback network. This is also known as shunt-driven shunt-fed feedback i.e., a parallel-parallel proto type.The below figure shows the block diagram of voltage shunt feedback, by which it is evident that the feedback circuit is placed in shunt with the output and also with the input.

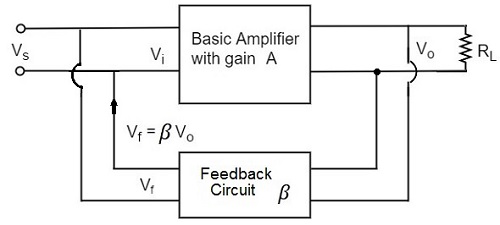Fig 5 Voltage Shunt FeedbackAs the feedback circuit is connected in shunt with the output and the input as well, both the output impedance and the input impedance are decreased.Q7) Derive Av, Ri, Ro for voltage series feedback amplifier?A7) Voltage series:

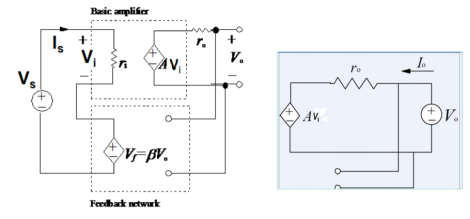Fig 7 Voltage Series FeedbackVoltage Gain :Vo = A.Vi Vf = β VoA(Vs – βVo) = Vo AVs = (1+βA) Vo Af = Vo/Vs = A/1+βA Input impedance Zin = Vs/Is = Vi+βAVi/Is Zin = Vi(1+β A ) /Is = ri(1+βA) Output Impedance Zout IVS=0 = Vo/Io Io = Vo – A. Vi / ro Vi + β.Vo = Vs Vi = - β Vo Io = Vo + AβVo/ro Zout = Vo/Io = ro / 1+AβQ8) Derive Av, Ri, Ro for voltage shunt feedback amplifier?A8) Voltage shunt feedback amplifier:

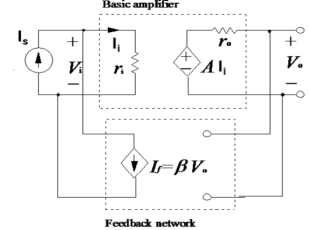Fig 6 Voltage shunt feedback networkVoltage gain: Vo =A.Ii = A(Is – If) If = β VoA(Is – β Vo ) = Vo A Is = (1+βA ) Vo Af = Vo/Is = A/ 1+βAInput Impedance Zin = Vi/Is = Vi/ Ii + If = Ii . ri / Ii + β A Ii Zin = ri / (1+βA)Output Impedance Zout IVS =0 = Vo/Io From input port Ii = -If = - β Vo From output port Io = Vo – A Ii/ro = Vo + βAVo/ro Zo = Vo /Io = ro/ (1+βA) Q9) Explain open loop frequency response of op-amp?A9) “Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz). This output gain decreases linearly with frequency down to “Unity Gain” or 1, at about 1MHz and this is shown in the following open loop gain response curve.Open-loop Frequency Response Curve

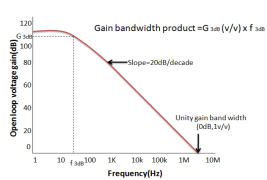Fig 10 Frequency Response CurveFrom this frequency response curve, we can see that the product of the gain against frequency is constant at any point along the curve. Also, that the unity gain (0dB) frequency also determines the gain of the amplifier at any point along the curve. This constant is generally known as the Gain Bandwidth Product or GBP. Therefore:GBP = Gain x Bandwidth = A x BWFor example, from the graph above the gain of the amplifier at 100kHz is given as 20dB or 10, then the gain bandwidth product is calculated as:GBP = A x BW = 10 x 100,000Hz = 1,000,000.Similarly, the operational amplifiers gain at 1kHz = 60dB or 1000, therefore the GBP is given as:GBP = A x BW = 1,000 x 1,000Hz = 1,000,000. The Voltage Gain (AV) of the operational amplifier can be found using the following formula:Av = Vout/ Vinand in Decibels or (dB) is given as:20 log (A) or 20 log (Vout/ Vin ) in dBAn Op- Amp BandwidthThe operational amplifiers bandwidth is the frequency range over which the voltage gain of the amplifier is above 70.7% or -3dB (where 0dB is the maximum) of its maximum output value.

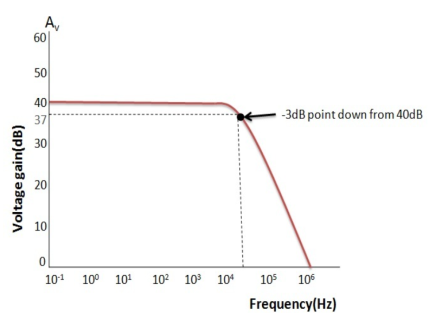Fig 11 Frequency ResponseQ10) Explain slew rate and also derive its expression?A10) The slew rate is a parameter that describes the operating speed of an op-amp. It represents the rate that can change per unit time stipulated by the output voltage. For example, 1V/us indicates that the voltage can change by 1V in 1μs. Ideal op-amps make it possible to faithfully output an output signal for any input signal. However, in reality slew rate limits do exist.When supplying a rectangular pulse at the input with a steep rise and fall, this indicates the possible degree of change in the output voltage per unit time.

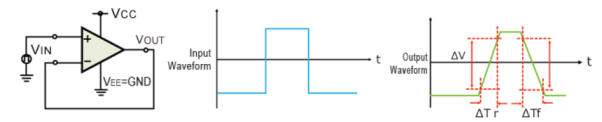Fig 14 Slew Rate calculationThe rise and fall slew rates are calculated by the following equations:SRr = ∆ V / ∆ Tr SRf = ∆ V / ∆ Tf

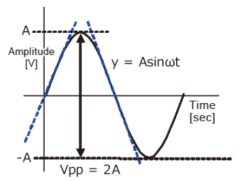Fig 15 Sinusoidal waveform Calculate the slew rate The output is given by y=AsinωtThe slew rate is the slope of the tangent of the sine wave, differentiating the above equation.

dy	/ = Aω cosωt		ωt=0
Dt

The slew rate isSR=Aω　ω=2πf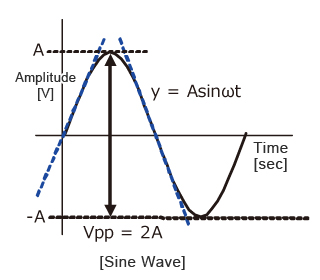

Fig 16 Sinusoidal Waveform Since the amplitude of the sine wave becomes Vpp=2A (peak-to-peak), the equation can be modified as follows.

This frequency(f) is referred to as the full power bandwidth. These are conditions where the amplification factor in the op-amp has not been set, in other words the relationship of the frequency and amplitude (within the output voltage range) that can be output by the op-amp in a voltage follower circuit.

Sign Up