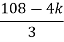undefined | unit 2 time response

Back to Study material

UNIT-2TIME RESPONSE Q1) The open loop transfer function of a system with unity feedback gain G (S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.A1) Finding closed loop transfer function,

C( S ) / R( S ) = G( S ) / 1 + G( S ) + H( S )

As it is unity feedback so, H(S) = 1

C(S)/R(S) = G(S)/1 + G(S)

= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4

C(S)/R(S) = 20/S2 + 5S + 24

Standard equation for second order system,

S2 + 2ξWnS + Wn2 = 0

We have,

S2 + 5S + 24 = 0

Wn2 = 24

Wn = 4.89 rad/sec

2ξWn = 5

(a). ξ = 5/2 x 4.89 = 0.511

(b). Mp% = e-∏ξ / √1 –ξ2 x 100

= e-∏ x 0.511 / √1 – (0.511)2 x 100

Mp% = 15.4%

(c). tr = ∏ - φ / Wd

φ = tan-1√1 – ξ2 / ξ

φ= tan-1√1 – (0.511)2 / (0.511)

φ = 1.03 rad.

tr = ∏ - 1.03/Wd

Wd = Wn√1 – ξ2

= 4.89 √1 – (0.511)2

Wd = 4.20 rad/sec

tr = ∏ - 1.03/4.20

tr = 502.34 msec

(d). tp = ∏/4.20 = 747.9 msec

Q2) A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Setteling time (v) Peak overshoot.A2) The closed loop transfer function is

C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2

= (5)2 / S2 + 2 x 0.7 x S + (5)2

C(S)/R(S) = 25 / S2 + 7s + 25

(ii). tp = ∏ / Wd

Wd = Wn√1 - ξ2

= 5√1 – (0.7)2

= 3.571 sec

(iii). tr = ∏ - φ/Wd

φ= tan-1√1 – ξ2 / ξ = 0.795 rad

tr = ∏ - 0.795 / 3.571

tr = 0.657 sec

(iv). For 2% settling time

ts = 4 / ξWn = 4 / 0.7 x 5

ts = 1.143 sec

(v). Mp = e-∏ξ / √1 –ξ2 x 100

Mp = 4.59%

Q3) The open loop transfer function of a unity feedback control system is given by G(S) = K/S(1 + ST). Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?A3)

C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1

C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)

C(S)/R(S) = K/S(1 + ST) + K

C(S)/R(S) = K/T / S2 + S/T + K/T

For second order system,

S2 + 2ξWnS + Wn2

2ξWn = 1/T

ξ = 1/2WnT

Wn2 = K/T

Wn =√K/T

ξ = 1 / 2√K/T T

ξ = 1 / 2 √KT

forξ1 = 0.2, for ξ2 = 0.4

ξ1 = 1 / 2 √K1T

ξ2 = 1 / 2 √K2T

ξ1/ ξ2 = √K2/K1

K2/K1 = (0.2/0.4)2

K2/K1 = 1 / 4

K1 = 4K2

Q4) Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2. Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?A4)

Mp = 5% = 0.05

Mp = e-∏ξ / √1 –ξ2

0.05 = e-∏ξ / √1 –ξ2

Cn 0.05 = - ∏ξ / √1 –ξ2

-2.99 = - ∏ξ / √1 –ξ2

8.97(1 – ξ2) = ξ2∏2

0.91 – 0.91 ξ2 = ξ2

0.91 = 1.91 ξ2

ξ2 = 0.69

(ii). ts = 4/ ξWn

4 = 4/ ξWn

Wn = 1/ ξ = 1/ 0.69

Wn = 1.45 rad/sec

Q5) for the given polynomials below determine the stability of the system S4+2S3+3S2+4S+5=0A5)

Arranging Coefficient in Rows.

S4	1	3	5
S3	2	4	0
S2	1	5	0
S1	-6	0	0
S0	5	0	0

For row S2 first term S2 =

= 1For row S2 Second termS2 =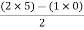

= 5For row S1: S1 =

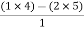= -6For row S0S0 =

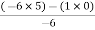= 5As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.Q6) Using Routh criterion determine the stability of the system with characteristic equation S4+8S3+18S2+16S+S = 0 A6) Arrange in rows.

S4	1	18	5
S3	8	16	0
S2	16	5
S1	13.5
S0	5

For row S2 first elementS1 =

= 16Second terms =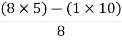

= 5For S1First element =

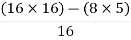= 13.5For S0 First element =

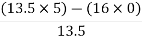= 5As there is no sign change for first column so all roots are is left half of S-plane and hence system is stable.Q7) Determine the stability of the system represent by following characteristic equations using Routh criterion1) S4 + 3s3 + 8s2 + 4s +3 = 02) S4 + 9s3 + 4S2 – 36s -32 = 0 A7)1) S4+3s3+8s2+4s+3=0

S4	1	8	3
S3	3	4	0
S2	6.66	3
S1	2.650	0
S0	3

No sign change in first column to no rows on right half of S-plane system stable.S4+9S3+4S2-36S-32 = 0

S4	1	4	-32
S3	9	-36	0
S2	8	-32
S1	0	0
S0

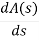Special case II of Routh Hurwitz criterion forming auxiliary equation A1 (s) = 8S2 – 32 = 0

= 16S – 0 =0

S4	1	4	-32
S3	9	-36	0
S2	8	-32
S1	16	0
S0	-32

One sign change so, one root lies on right half S-plane hence system is unstable.Q8) For using feedback open loop transfer function G(s) =

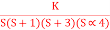find range of k for stabilityA8) Findlay characteristics equation.

CE = 1+G (s) H(s) = 0

H(s) =1 using feedback

CE = 1+ G(s)

1+ = 0

S(S+1)(S+3)(S+4)+k = 0

(S2+5)(S2+7Sα12)αK = 0

S4α7S3α1252+S3α7S2α125αK = 0

S4+8S3α19S2+125+k = 0

By Routh Hurwitz Criterion

S4	1	19	K
S3	8	12	0
S2	17.5	K
S1		0
S0	k

For system to be stable the range of K is 0< K <

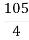.Q9) The characteristic equation for certain feedback control system is given. Find range of K for system to be stable.

S4	1	12	K
S3	4	36
S2	3	K
S1
S0	K

A9)

S4+4S3α12S2+36SαK = 0

For stability K>0

> 0

K < 27

Range of K will be 0 < K < 27

Q10) Check if all roots of equation S3+6S2+25S+38 = 0, have real poll more negative than -1.A10)

S3	1	25
S2	6	38
S1	18.67
S0	38

No sign change in first column, hence all roots are in left half of S-plane.

Replacing S = Z-1. In above equation

(Z-1)3+6(Z-1)2+25(Z-1)+38 = 0

Z3+ Z23+16Z+18=0

Z3	1	16
Z2	3	18
Z1	10
Z0	18

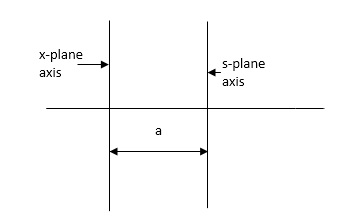
No sign change in first column roots lie on left half of Z-plane hence all roots of original equation in S-domain lie to left half 0f S = -1Q11) Explain relative stability?A11) Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.

Fig 1 Location of Pole for relative stabilityThe above fig 1 shows the characteristic equation is modified by shifting the origin of S-plane to S1= -

.S = Z-S1After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane

Sign Up