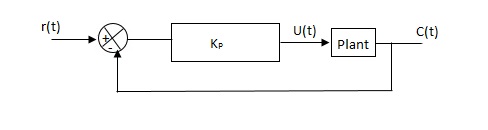
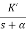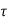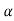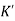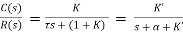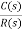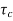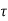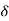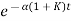|
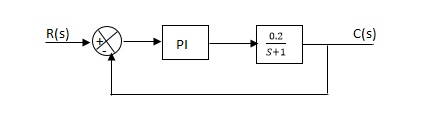
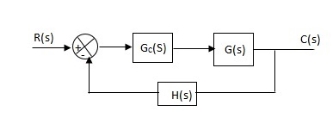
(a). Without : C(S)/R(S) = 0.2/(S + 1) C(S) = R(S) 0.2/(S + 1) + 0.2 For unit step ess = 1/1 + Kp Kp = lt G(S) S 0 = lt 0.2/(S + 1) S 0 Kp = 0.2 ess = 1/1.2 = 5/6 = 0.8 (b). With controller : Gc(S) = Kp + Ki/S G’(S) = Gc(S).G(S) = ( Kp + Ki/S )0.2/(S + 1) = (KpS + Ki)0.2/S(S + 1) ess = 1/1 + Kp = 0 So, the value of ess is decreased. (b). Given Kpi/Kp = 0.1 G’(S) = (Kp + Ki/S)(0.2/S + 1) = (KpS + Ki)0.2/S(S + 1) As a pole is to be added so, we have to examine the CE, 1 + G’(S) = 0 1 + (Kp + Ki)0.2/S(S + 1) = 0 S2 + S + 0.2KpS + 0.2Ki = 0 S2 + (0.2Kp + 1)S + 0.2Ki = 0 Given, Kpi = 0.1Ki Kp = 10Ki
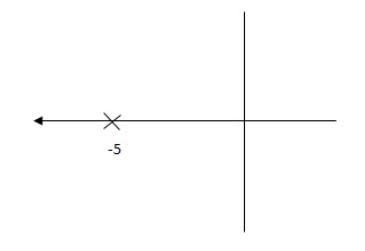
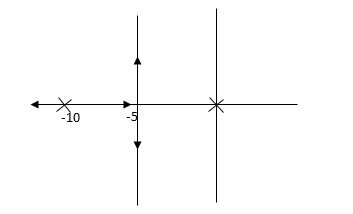
S2 + (2Ki + 1)S + 0.2Ki = 0 Pole at S = -5 25 + (2Ki + 1)(-5) + 0.2Ki = 0 -10Ki – 5 + 25 + 0.2Ki = 0 -9.8Ki = -20 Ki = 2.05 Kp = 10Ki = 20.5
Now, G’(S) = (KpS + Ki)(0.2)/S(S + 1) = (20.5S + 2.05)(0.2)/S(S + 1) G’(S) = 4.1S + 0.41/S(S + 1) |
|
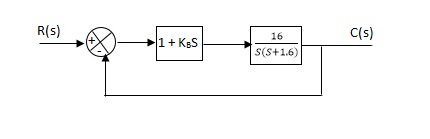
(1). Kp = 1 Without controller:- C(S)/R(S) = 16/S2 + 1.6S + 16 wn = 4 2 ξwn = 16 ξ = 1.6/2 x 4 = 0.2
(b). With derivative :- ξS = 0.2 to 0.8 undamped to critically damped, G’(S) = (1 + KdS)(16)/(S2 + 1.6S)
CE: S2 + 1.6S + 16(1 + KdS) = 0 S2 + (1.6 + Kd)S + 16 = 0 2 ξwn = 1.6 + Kd1.6 wn = 4 ξS = 0.8 2 x 4 x 0.8 = 1.6 + Kd1.6 6.4 – 1.6 = Kd1.6 4.8/16 = Kd Kd = 0.3 TF = (1 + 0.3S)16/S(S + 16)
|
|
|
|
|
|
|
|
|
|
w2n = 1 wn = 1 2ξWn = 8 ξ = 4 ξ>/1 so, overdamped. Now introducing Gc(S) = K G’(S) = Kp/S(S + 8) CLTF = Kp/S2 + 8S + Kp wn = √Kp 2 ξwn = 8 ξ = 4/√Kp If, Kp = 16; ξ = 1; critically damped Kp> 16; ξ< 1; undamped Kp< 16; ξ> 1; overdamped |
G(s) = Let K =
The poles for the above system lie at s= - The dc gain of the system is given by G(0) = K = For closed loop system the transfer function is given by
|
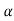 to (–
to (–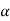 +K’). Due to this change the dynamic response of the system is also affected. For studying the dynamic response, we assume that the input to the system is an impulse.
+K’). Due to this change the dynamic response of the system is also affected. For studying the dynamic response, we assume that the input to the system is an impulse.r(t) = And it can also be written as R(s) = 1 Taking inverse Laplace transform of equation 1 we get For open loop system c(t) = K’ Taking inverse Laplace transform of equation 2 we get For closed loop system c(t) = K’ |
 =
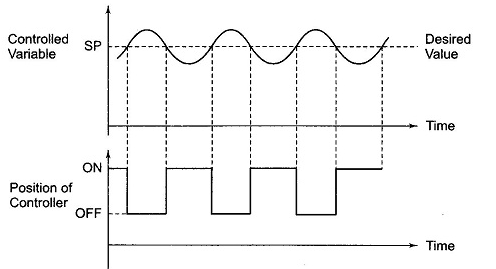
= 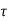 /(1+K) so its response decays faster than open loop system by factor of (1+K).Q10) Explain Ziegler Nichols method for tuning of controllers?A10)
/(1+K) so its response decays faster than open loop system by factor of (1+K).Q10) Explain Ziegler Nichols method for tuning of controllers?A10)
|
|
 delay time -L calculated by drawingtime constant -j tangent c(s) / l(s) = ke-l1s / ts+1 The values of KP, Ti and td should be set according to the table suggested by Ziegler Nichols tuning rules shown below.Type of controller
delay time -L calculated by drawingtime constant -j tangent c(s) / l(s) = ke-l1s / ts+1 The values of KP, Ti and td should be set according to the table suggested by Ziegler Nichols tuning rules shown below.Type of controllerTypes of controller | Kp | Ti | Td |
|
P | T/L | 00 | 0 |
|
PI | 0.9T/L | L/0.3 | 0 |
|
PID | 1.2T/L | 2L | 0.5L |
|
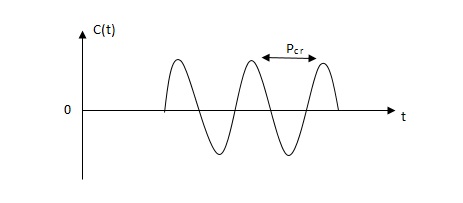
 and Td=02) use proportional control action only, increase kp from 0 to Kcr (Critical value).3)then Kcr and pcr (period) are determined experimentally.
and Td=02) use proportional control action only, increase kp from 0 to Kcr (Critical value).3)then Kcr and pcr (period) are determined experimentally.
|
|
Types of controller | KP | TI | Td |
P | 0.5Kcr |
| 0 |
PI | 0.45 KCR | 1/1.2PCR | 0 |
PID | 0.6KCR | 0.5PCR | 0.125PCR |
|
|
|
|
GC(S) = KP(1.1/Tis+Tds) =0.6 Kcr(1+1/0.5PcrS+ 0.125 PCRS) =0.075 KcrPcr(s+4/Pcr)2 / s
Thus, the PID controller has a pole at the origin and double zeros at s= -4/Pcr
| |||