UNIT - 1
DFT and FFT
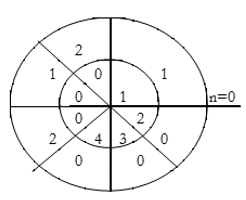
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) =  e-j2 π nk/N
e-j2 π nk/N
X(0) =
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) =  e-j2 π nk/N
e-j2 π nk/N
X(1) = 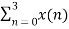 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 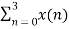 e-j2 π n2/4
e-j2 π n2/4
X(2) = 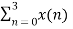 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) = 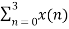 e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
2. For N =4 and
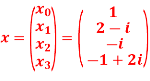
Calculate the DFT of x .
Solution:
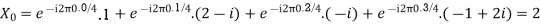
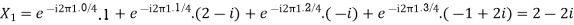
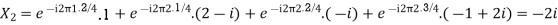

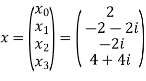
3. Compute the N-point DFT of x(n)=3δ(n).

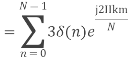


4. Compute the N-point DFT of x(n)=7(n−n0)
Solution − We know that,
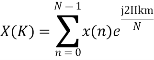
Substituting the value of x(n),
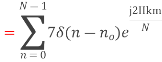
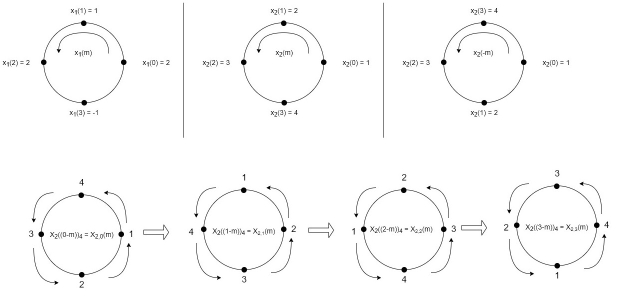
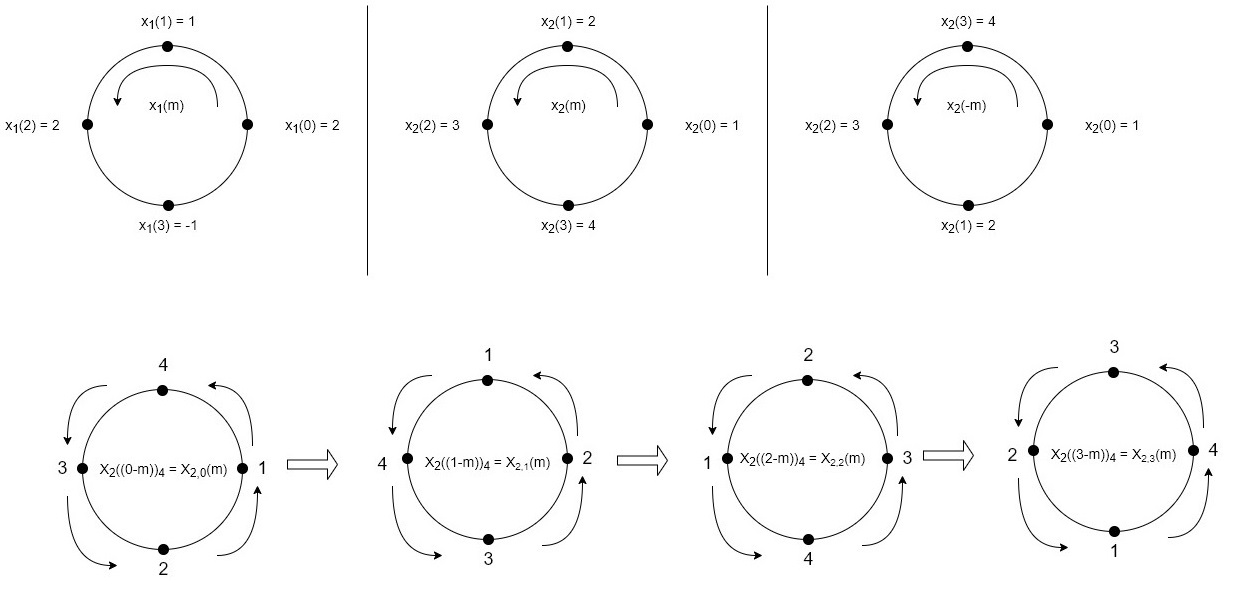
5. Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

(2)
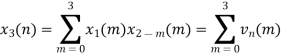
When n=0; 

The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
When n=1; 
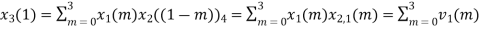
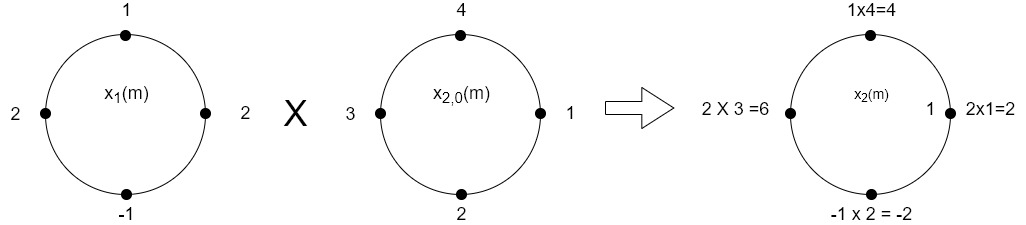
The sum of samples of v1(m) gives x2(1)
⸫ x3(1)=4 + 1 +8-3=10
(3)When n=2; 
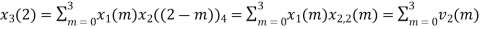
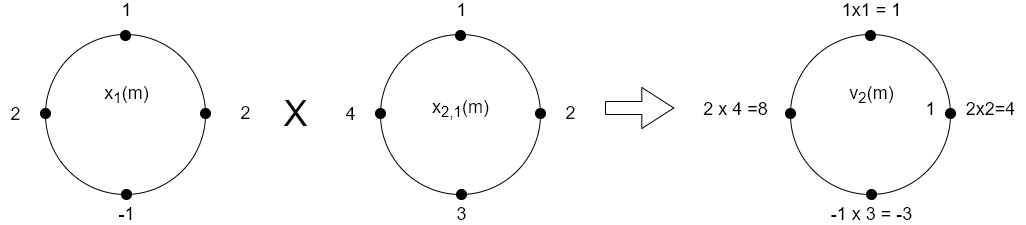
The sum of samples of v2(m) gives x3(2)
⸫ x3(2)=6+2+2-4=6
(4) When n=3; 
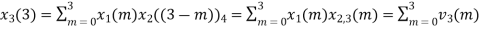
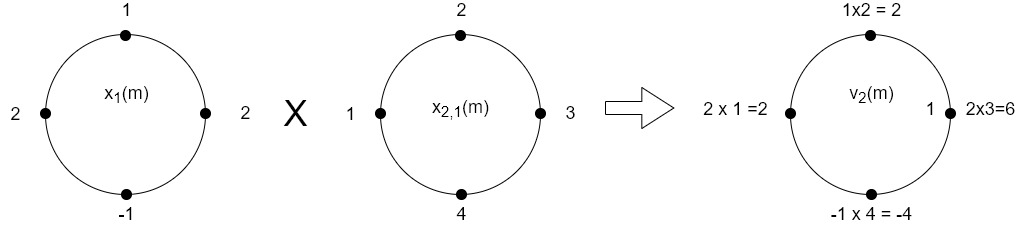
The sum of samples of v3(m) gives x3(3)
⸫ x3(3)=8+ 3+ 4-1= 14
x3(n)={10,10,6,14}


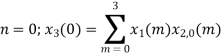
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
6. h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).
Solution:
Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))
Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1



7. Find circular convolution and linear using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
Solution:
Circular convolution using circular convolution:
x1x1(n) = {1, 2, 3, 4}
and x2x2 (n) = {1, 2, 1, 2}
L=4, M=4
Length of y(n) = L+M-1=4+4-1=7
∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}
& x2(n) = {1, 2, 1, 2, 0, 0, 0}
For y(0),
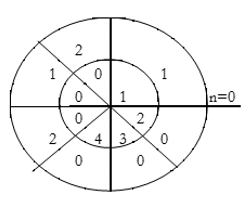
∴ y(0)= 1×1=1
For y(1),
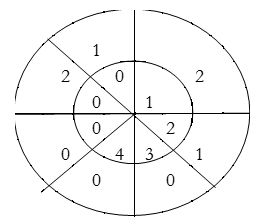
∴ y(1)= 2×1+1×2=4
For y(2),
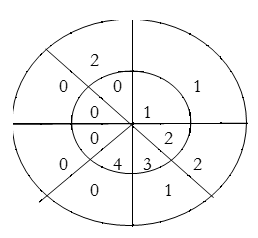
∴ y(2)= 1×1+2×2+3×1=8
For y(3),
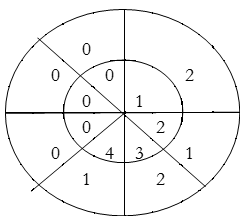
y(3)=1×2+2×1+3×2+4×1=14
For y(4),
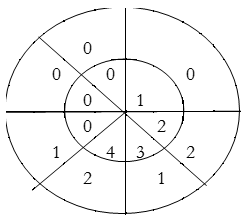
∴ y(4)= 4×2+3×1+2×2=15
For y(5),
∴ y(5) = 4×1+3×2=10
For y(6),
∴ y(6) = 4×2=8
∴y(n) = {1, 4, 8, 14, 15, 10, 8}
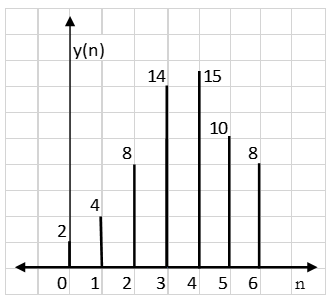
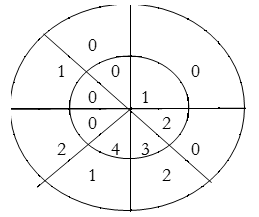
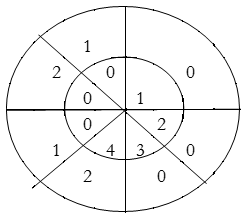
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}
For y(0),
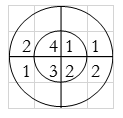
∴ y(0)= 1+4+3+8=16
For y(1),
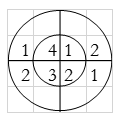
∴ y(1)= 2+2+6+4=14
For y(2),
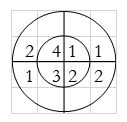
∴ y(2)= 1+4+3+8=16
For y(3),
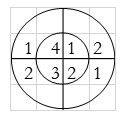
∴ y(3)= 2+2+6+4=14
y(n) = {16, 14, 16, 14}
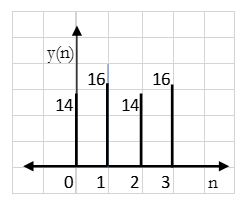
Result: y(n) = {14, 16, 14, 16}
8. Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
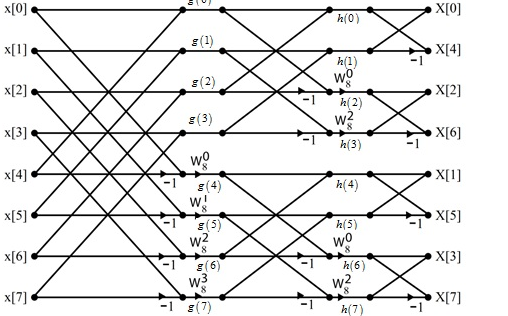
X(0)= 20 X(4) =0
X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141
X(2) = 0 X(6) = 0
X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142
9. Explain overlap add method.
Break the input signal x(n) into non overlapping blocks  of length L.
of length L.
Zero pad h(n) to be of length N=L+M-1.
Take N-DFT of h(n) to give H(k), k = 0,1,…,N-1.
Fop each block m
Zero pad 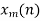 to be length of N-L+M-1.
to be length of N-L+M-1.
Take N-DFT of 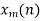 to give
to give 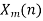 , k=0,1,…,N-1.
, k=0,1,…,N-1.
Multiply 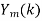 =
=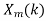 . H(k), k=0,1,…,N-1.
. H(k), k=0,1,…,N-1.
Take N-DFT of 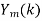 to give
to give 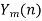 , n=0,1,…,N-1.
, n=0,1,…,N-1.
Form y(n) by overlapping the last M-1 samples of  with the first M-1 samples of
with the first M-1 samples of  and adding the result.
and adding the result.
10. Explain overlap save method.

- Take N-DFT of to give
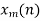 , k= 0,1,…,N-1.
, k= 0,1,…,N-1.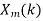
- Multiply =
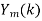 . H (k), k=0,1,…,N-1.
. H (k), k=0,1,…,N-1.
- Take N-DFT of to give
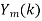 , n=0,1,…,N-1.
, n=0,1,…,N-1.
- Discard the first M-1 points of each output block .