undefined | unit 6 design for testability

Back to Study material

VLSI

Unit 6

Design for Testability

Q1) What is fault model?

A1) A fault model is an engineering model that could go wrong in the construction or operation of a piece of equipment.

From the model, the designer or user can then predict the consequences of this particular fault.

Fault models can be used in almost all branches of engineering.

Basic fault models in digital circuits include:

Static faults, which give incorrect values at any speed and sensitized by performing only one operation:

The stuck-at fault model.

In this, a signal, or gate output, is stuck at a 0 or 1 value, independent of the inputs to the circuit.

The bridging fault model.

Here, two signals are connected together when they should not be. Depending on the logic circuitry employed, this may result in a wired-OR or wired-AND logic function. Since there are O(n2) potential bridging faults, they are normally restricted to signals that are physically adjacent in the design.

The transistor faults.

This model describes faults for CMOS logic gates. At transistor level, a transistor maybe stuck-short or stuck-open. In stuck-short, a transistor behaves as it is always conducts (or stuck-on), and stuck-open is when a transistor never conducts current (or stuck-off). Stuck-short will produce a short between VDD and VSS.

The open fault model.

Here a wire is assumed broken, and one or more inputs are disconnected from the output that should drive them. As with bridging faults, the resulting behavior depends on the circuit implementation.

Dynamic faults, only at-speed and are sensitized by performing multiple operations sequentially:

The transition delay fault (or transition fault) model, where the signal eventually assumes the correct value, but more slowly (or rarely, more quickly) than normal.

Small-delay-defect mode

Q2) Explain the need for testability?

A2)

DFT is a technique, which facilitates a design to become testable after fabrication. Add on logic is added along with the design logic during implementation process helps in post-production testing.

Post-production testing is necessary because, the process of manufacturing is not 100% error free.

There are defects in silicon which contribute towards the errors introduced in the physical device.

A chip will not work as per the specifications if there are any errors introduced in fabrication.

All the functional tests run on each of a million physical devices, is very time consuming, there was a need for a method, which assures it's maturity without running full exhaustive tests on the physical device in order to ensure that the device has been manufactured correctly.

Q3) Explain path sensitizing?

A3)

The basic principle of the path sensitization method is to choose some path from the origin of the fault to the circuit output. A path is sensitized if the inputs to the gates along the path are assigned values such that the effect of the fault can be propagated to the output.

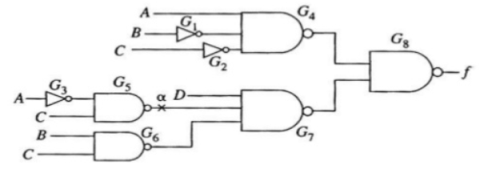
Diagram

Description automatically generated

Figure. Path Sensitizing

From the above fig. Assume that the line α is s-a-1.

Hence to test for α, both G3 = C = 1. Also D = G6 =1 so that G7 =1 if the fault is absent. To propagate the fault from G7 to output f via G8 requires G4 = 1.

This is because if G4 = 0 then output f will be forced to be 1.

The process of propagating the effect of the fault from its original location to the circuit output is known as forward trace.

Similar is the process of backward trace.

Q4) Explain random tests?

Random pattern testing has been a common practice in industry for a long time. It was recognized quite early in the development of test generation strategies that there is a lot to be gained if a short random test precedes the long and laborious deterministic test.

A random test is defined as a random selection of input vectors. The input vectors may or may not be equally likely. A random test is said to be uniform if all input vectors are equally probable, and said to be biased otherwise. It is important to note that no test is truly random. The reason is that no ideal random number generator exists.

Q5) Explain BIST?

A5) As the complexity of VLSI circuits increases, test generation and application becomes an expensive and not always very effective means of testing. Built-in Self Test (BIST) is another solution.

It is a mechanism that permits a machine to test itself. Engineers design BISTs to meet requirements such as:

high reliability

lower repair cycle times

or constraints such as:

limited technician accessibility

cost of testing during manufacture

The main purposeof BIST is to reduce the complexity, and thereby decrease the cost and reduce reliance upon external (pattern-programmed) test equipment.

It reduces cost in two ways:

reduces test-cycle duration

reduces the complexity of the test/probe setup, by reducing the number of I/O signals that must be driven/examined under tester control.

Figure below shows the Built-in Self Test system.

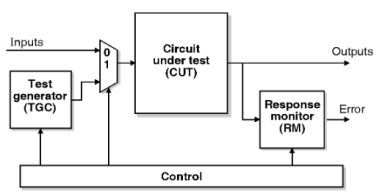
Diagram

Description automatically generated

Figure. BIST

Q6) What is boundary scan test?

A6) In boundary scan test we design the chip to increase observability and controllability

If each register could be observed and controlled, test problem reduces to testing combinational logic between registers.

The logic blocks enter the test mode where they generate test patterns and report the results automatically.

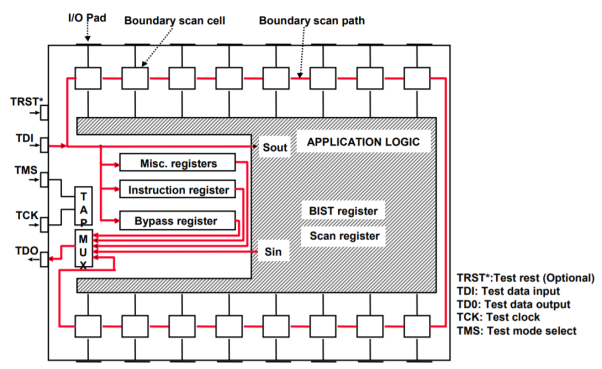
Diagram

Description automatically generated

Figure. Boundary scan

Q7) What is fault coverage?

A7) Fault Coverage contains the percentage of faults detected from all the faults of the test patterns generated by the tool

FC = DT + (PD * posdet_credit) / Total faults x 100

where DT is the detected faults class which includes all the faults that the ATPG identifies as detected and this are classified into two groups

Det_simulation (DS)

Det_implication (DI)

PD – posdet or possible detected fault class includes all the faults that fault simulation identifies as possible detected but not hard to detect

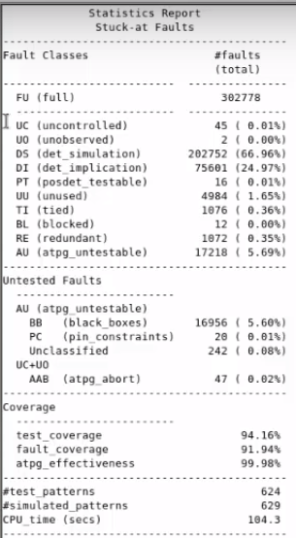
Table

Description automatically generated

Figure. Report_statistics of faults

From the report Total no of faults are given as 302778
Faults due to unused pins (UU), Tied pins (TI), Blocked Pins (BL), and redundant logic (RE) are untestable by tool and this faults must be excluded from the total number of faults while calculating the Test Coverage and considered while calculating the Fault Coverage.

UU+TI+BL+RE => 4984+1076+12+1072 = 7144

Thus Testable faults are given asTotal Faults – (UU+TI+BL+RE)
Total faults detected during simulation (DS) and implication (DI) are

DS +DI => 202752+75601+16 = 278369

In generalposdet_credit will be set to zero and with this above faults numbers we can have Test Coverage and Fault Coverage

TC = DT +0 / Testable faults x 100

TC = 278369/ 302778-7144 x 100

TC = 94.16 %

FC = DT +0/ Total faults x 100

FC = 278369/302778 x 100

FC = 91.94%

In this process TC and FC are calculated and we need to achieve 99 % Test Coverage for Stuck At fault model and 95% Test Coverage for At Speed fault model.

Q8) What is stuck at fault model?

A8) With a stuck at fault model we apply a structural test approach. Instead of testing all combination of 1’s and 0’s to a VLSI device, we test with a reduced set of test vectors.

Stuck at Fault Models operate at the logic model of digital circuits. An input or an output can be Stuck at Zero (S@0) or Stuck at One (S@1).

Its use three digital circuits to illustrate: Inverter, NAND, NOR. In CMOS technology, these logic gates can be found in most logic functions.

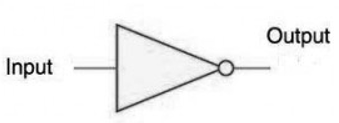
A pair of scissors

Description automatically generated with low confidence

Logic table

A	D
0	1
1	0

Inverter Stuck faults list: A S@0,A S@1, D S@0, D S@1

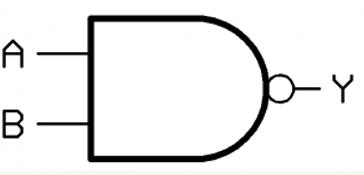
Shape

Description automatically generated

A	B	Y
1	0	1
1	1	0
0	0	1
0	1	1

NAND Stuck faults list: A S@0,A S@1, BS@0, B S@1, CS@0, C S @1

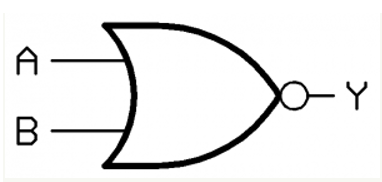
Venn diagram

Description automatically generated

NOR Logic Table

A	B	Y
1	0	1
1	1	0
0	0	1
0	1	1

NOR Stuck faults list: A S@0, A S@1, B S@0, B S@1, C S@0, C S@1

Q9) Explain stuck open and stuck short faults?

A9) Consider a 2-input NOR gate:

Stuck-At faults include: A-SA0 , B-SA0 , Out-SA0 and Out-SA1 .

SOP model adds three non-classical faults:

A-Stuck-Open ( A-SOP ),
B-Stuck-Open ( B-SOP )
Vdd-Stuck-Open ( VDD-SOP).

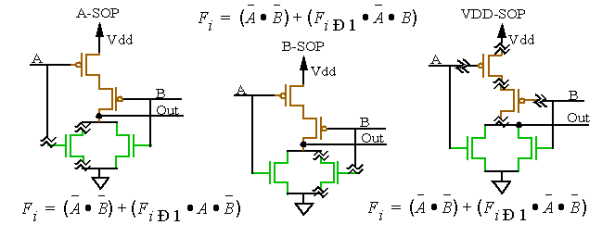
A picture containing text, clock

Description automatically generated

Figure. SOP model

Stuck-Open Faults

Exhaustive test AB = (00, 01, 10, 11) does not detect all faults.

For SOP, vector order is important.

For example, the sequence AB = (00, 01, 00, 10) is able to detect all faults on the NOR gate, including the SOP faults.

This test sequence tests each path between the output and VDD and GND independently.

The tests are really test sequences.

First pattern initializes the output node, second pattern checks for the presence of the fault.

Stuck-Open Faults

Switch-level test generation algorithms can automate the generation of these tests.

A gate level model is also possible:

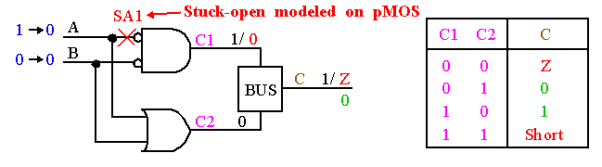
A picture containing text, clock, time, dark

Description automatically generated

Figure . Stuck open model

Series connections of transistors are replaced with AND, parallel connections are replaced with OR.

pMOS inputs are inverted.

When the 2 inputs to BUS are different, output determined by C1.

In fault free circuit, this must be true rsince complementary logic functions drive BUS.

Stuck-short (Stuck-on) Faults

Complement of the Stuck-Open fault model is the Stuck-On fault model.

Stuck-On faulty gate output is difficult to predict.

A transistor that is permanently stuck-on will, for some input combination(s), compete with its complementary transistors for control of the output.

Sometimes this competition does not result in a catastrophic failure.

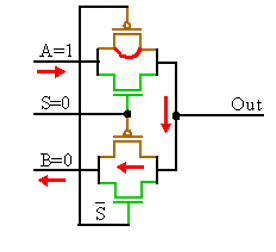
Diagram, schematic

Description automatically generated

Figure. Stuck ON

The output value depends on driving transistor resistances. Strength of upstream drivers. Delay fault is likely if functional behaviour is preserved. IDDQ test guarantees detection.

Stuck-short faults modeled as SA0 on pMOS in gate-level equivalent model.

Q10) Explain boundary scan test?

A10) Boundary-scan cells in a device can capture data from integrated circuit line, or force data onto them. In this way a test system that can input a data stream to the shift register chain can set up states on the board, and also monitor data. By setting up one serial data stream, latching this into place, and then monitor the returning data stream, it is possible to gain access to the circuits on the board and check that a returning data stream is what is expected. If it is, then the test can pass, but if not the boundary scan system has detected and problem that can be further investigated.

Q11) Explain JTAG technology?

A11) The JTAG, boundary scan test technique uses a shift register latch cell built into each external connection of every boundary scan compatible device. One boundary scan cell is included in the integrated circuit line adjacent to each I/O pin, and when used in the shift register mode it can transfer data along to the next cell in the device. There are defined entry and exit points for the data to enter and exit the device, and it is therefore possible to chain several devices together.

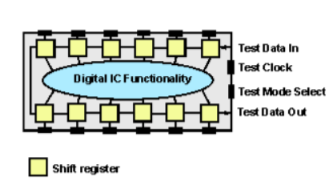
Diagram

Description automatically generated

Figure. JTAG technology

Under normal operating conditions the cell is set so that it has no effect and it becomes invisible. However when the device is set to test mode, it permits a serial data stream (test vector) to be passed from one shift register latch cell to the next.

JTAG Interface

There are a number of JTAG control and data lines that form the test access port, TAP. These lines known as TCK, TMS and the optional TRST line are connected in parallel to the chips in the boundary scan chain. Connections designated TDI (input) and TDO (output) are daisy chained together to provide a path around the boundary scan chips for the data. Data is sent into the TDI of the first chip, and then TDO from the first chip is connected to TDI of the next and so forth. Finally the data is taken from the TDO of the last IC in the daisy chain.

TAP, Test Access Port - The pins associated with the test access controller.

TCK, Test Clock - this pin is the clock signal used for ensuring the timing of the boundary scan system. The TDI shifts values into the appropriate register on the rising edge of TCK. The selected register contents shift out onto TDO on the falling edge of TCK.

TDI, Test Data Input - Test instructions shift into the device through this pin.

TDO, Test Data Output - This pin provides data from the boundary scan registers, i.e. test data shifts out on this pin.

TMS, Test Mode Select - This input which also clocks through on the rising edge of TCK determines the state of the TAP controller.

TRST, Test Reset - This is an optional active low test reset pin. It permits asynchronous TAP controller initialization without affecting other device or system logic.

Application:

It is used in a variety of other test scenarios, including product development and debugging as well as field service

Q12) Explain TAP controller?

A12) The TAP controller is a finite state machine that responds to changes at the TMS and TCK signals of the TAP and controls the sequence of operations of the circuitry defined by standard. It also controls the scanning of data into the various registers of the JTAG architecture. Two state transition paths for scanning the signal at TDI, one for shifting to the instruction register and one for shifting data into the active data register. The state diagram is shown in figure below. All state transitions of the TAP controller shall occur based on the value of TMS at the time of a rising edge of TCK. Actions of the test logic shall occur on either the rising or the falling edge of TCK in each controller state. The behavior of the TAP controller and other test logic in each of the controller states is briefly described as follows.

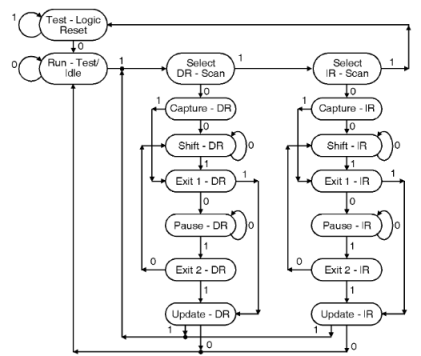
Diagram

Description automatically generated

Figure . TAP controller

Test-Logic-Reset: This state is entered on power-up of the device.

Run-Test-Idle: This state allows certain operations to occur depending on the current instruction.

Select-DR-Scan: This state is entered prior to performing a scan operation on a data register.

Select-IR-Scan: This state is entered prior to performing a scan operation on the instruction register.

Capture-DR: This state allows data register selected by the current instruction on the rising edge of TCK.

Shift-DR: This state shifts the data, in the currently selected register.

Exit1-DR: This state allows the option of passing on to the Pause-DR state.

Pause-DR: This wait state allows shifting of data to be temporarily halted.

Exit2-DR: This state allows the option of passing on to the Update-DR state.

Update-DR: This state causes data contained in the currently selected data register to be loaded into a latched parallel output.

Capture-IR: This state allows data to be loaded from parallel inputs into the instruction register.

Shift-IR: This shifts the values in the instruction register towards TDO.

Exit1-IR: This state allows the option of passing on to the Pause-IR state.

Pause-IR: This wait state that allows shifting of the instruction to be halted.

Exit2-IR: This state allows the option of passing on to the Update-IR state.

Update-IR: This state causes the values contained in the instruction register to be loaded into a latched parallel output on the falling edge of TCK after entering this state.

Sign Up