Question Bank

UNIT–3

Question Bank

UNIT–3

Question-1: Find the fourier series of the function f(x) = x      where 0 < x < 2 π

Sol. We know that, from fourier series,

f(x) =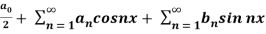

First we will find ,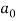

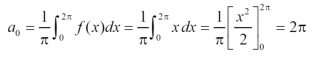
Now,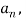

And ,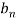

Put these value in fourier series, we get

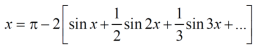
Question-2: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π

And has period 2π

Sol. First we will find

  = 

                                                   =

                                                   =

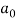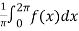
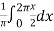
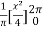
                                                  = π

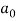   =   π

Similarly,

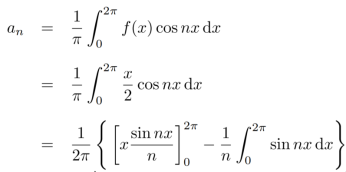
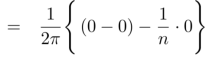
Which gives, 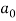   =   0

Now,

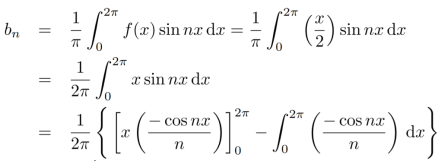
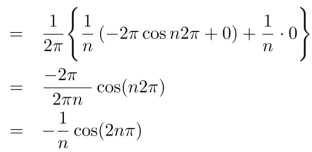
We get,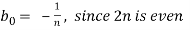

We know that, the fourier series

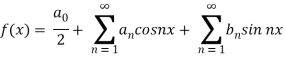
Put these values in fourier series, we get

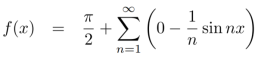
Question-3: Define even and odd functions.

Sol.

Odd function-

A function f(x), which is written as ,

f( - x ) = - f(x)

Is known as odd function.

The graph of the odd function looks like-

Tha graph of the function is symmetric about x-axis.

And the area under the curve from -π to π is always zero.(see fig)

Even function-

If f(-x) = f(x) then the function is known as even function.

The graph of the function f(x) looks like-

Area under the curve from -π to π  will always be double the area from 0 to π

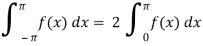
Question-4: Find the fourier expression of f(x) = x³ for –π< x <π.

Sol.

Here, we can see that f(x) Is an odd function

So that,

and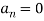

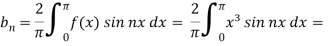
We will use here ,

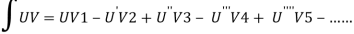
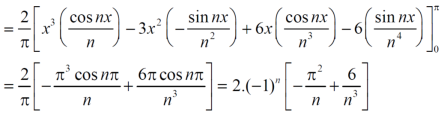
We get the value of f(x),

Question-5: Find the Fourier series expansion of the periodic function of period 2π.

f(x) = x² ,    -π≤x≤π

Sol. The given function is even, so that,

We will find

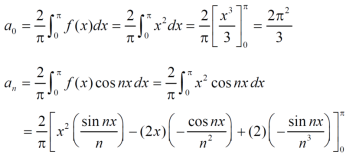
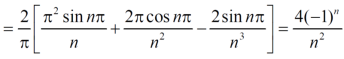
The fourier series will be ,

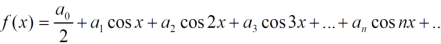
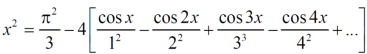
Question-6: Find a Fourier series for

;

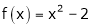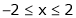
Solution:

Here

;

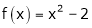Since f(x) is even function hence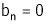

It’s Fourier series is

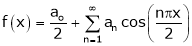… (1)

Where

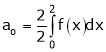
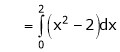
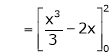
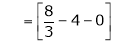
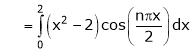
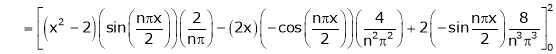
Hence equation (1) becomes,

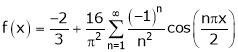
Question-7: Find the Fourier sine series for the function-

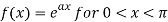
Where ‘a’ is a constant.

Sol. Here we know-

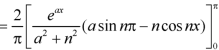
We know that-

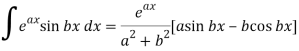
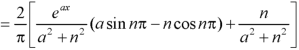
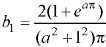
And

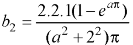
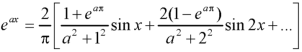
Question-8: Find the constant terms and the coefficients of the first sine and cosine terms in the Fourier series of f(x) of the following table-

Sol.

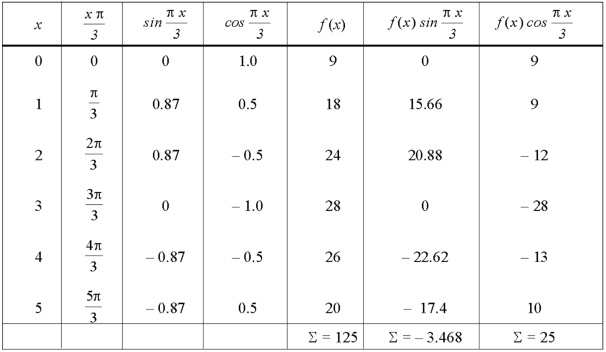
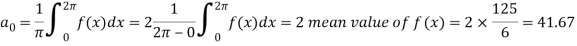
Fourier series is-

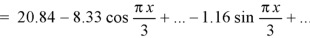
Question-9: Define Drichlet’sconditoons for the representation of Fourier series.

Sol.

Dirichlet’s conditions for representation by a Fourier series-

Let f(x) be a function defined in C < x < C + 2L such that

1)     f(x) is defined and single valued in the given internal also. 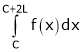exist.

2)     f(x) may have finite number of finite discontinuities in the interval.

3)     f(x) may have finite number of maxima or minima in the given interval.