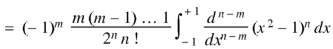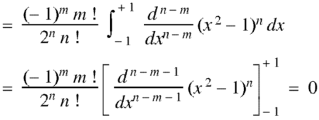Question Bank

UNIT–5

Question Bank

UNIT–5

Question-1: Define Bessel function.

Sol.The Bessel equation is-

The solution of this equations will be-

The Bessel function is denoted by and defined as-

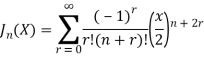
If we put n = 0 then Bessel function becomes-

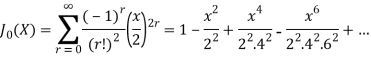
Now if n = 1, then-

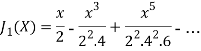
The graph of these two equations will be-

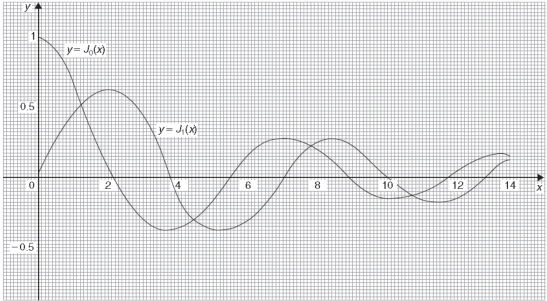
General solution of Bessel equation-

Question-2: Prove that-

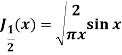
Sol.

As we know that-

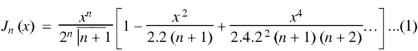
Now put n = 1/2 in equation (1), then we get-

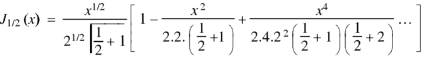
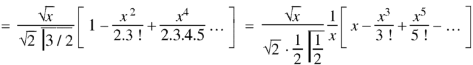
Hence proved.

Question-3: Prove that-

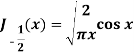
Sol.

Put n = -1/2 in equation (1) of the above question, we get-

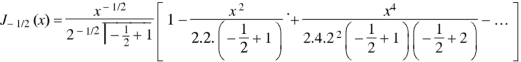
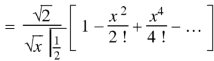
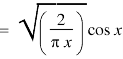
Question-4: Prove that-

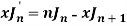
Sol.

As we know that-

On differentiating with respect to x, we obtain-

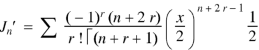
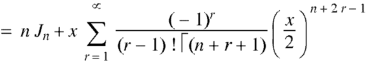
Putting r – 1 = s

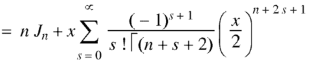
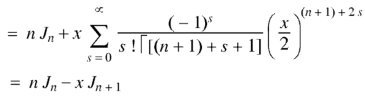
Question-5: Show that-

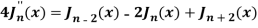
By using recurrence relation.

Sol.

We know that-

The recurrence formula-

On differentiating, we get-

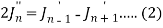
Now replace n by n -1 and n by n+1 in (1), we have-

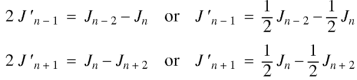
Put the values of and 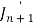from the above equations in (2), we get-

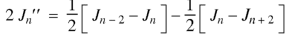
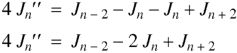
Question-6: Prove that-

Sol.

We know that- from recurrence formula

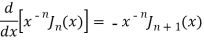
On integrating we get-

On taking n = 2 in (1), we get-

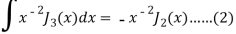
Again-

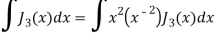
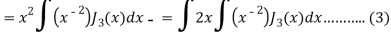
Put the value of from equation (2) and (3), we get-

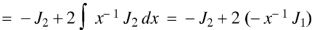
By equation (1), when n = 1

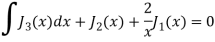
Question-7: Prove that is the coefficient of 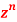in the expansion of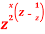

Proof:

As we know that-

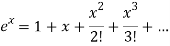
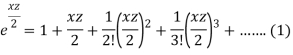
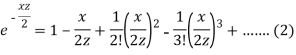
Multiply equation (1) by (2), we get-

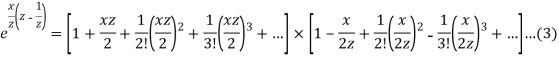
Now the coefficient of 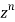in the product of (3)

=

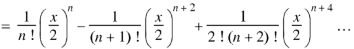
Similarly the coefficient of in the product of (3) =

So that-

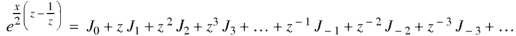
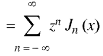
That is why 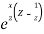is known as the generating function of Bessel functions

Question-8: Express in terms of Legendre polynomials.

Sol.

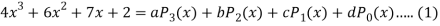
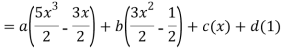
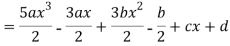
By equating the coefficients of like powers of x, we get-

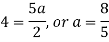
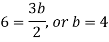
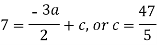
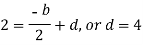
Put these values in equation (1), we get-

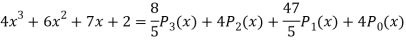
Question-9: Let be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-

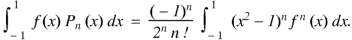
Sol.

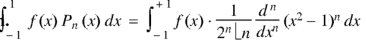
We know that-

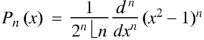
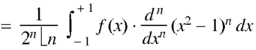
On integrating by parts, we get-

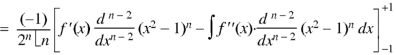
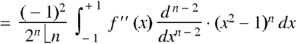
Now integrate (n – 2) times by parts, we get-

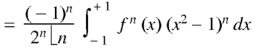
Question-10: Show that-

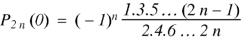
Sol.

We know that

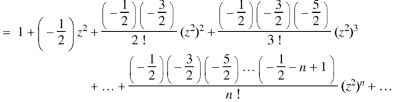
Equating the coefficients of both sides, we have-

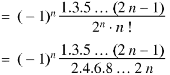
Question-11: Prove that-

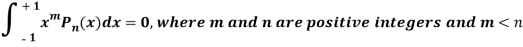
Sol.

By using Rodrigue formula for Legendre function.

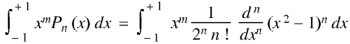
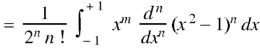
On integrating by parts, we get-

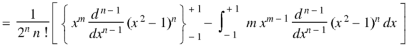
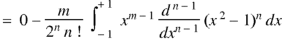
Now integrating m – 2 times, we get-