Unit 1
Fundamental Concepts of Financial Mathematics
Q1) Consider the following two investment strategies: A and B. Scheme A pays a 12 percent interest rate that is compounded annually. With monthly compounding, Scheme B pays 11.5 percent interest. Calculate the two investments' effective interest rates. Which scheme do you think you'd go with?
A1)
Scheme A's effective rate of interest is the same as its nominal rate of interest, which is 12 percent. Scheme B's effective rate of interest is
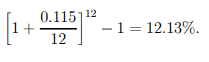
Despite the fact that Scheme A has a higher nominal interest rate, Scheme B has a higher effective rate of interest. As a result, while a $100 investment in Scheme A will yield $12 in interest after a year, a $100 investment in Scheme B will yield $12.13 in interest for the same time span. As a result, Scheme B is the preferred choice.
Another benefit of the effective rate of interest is that it can be used to calculate the cumulative amount without regard to the average rate for assets that last longer than a year.
Q2) State basic rules of proportions?
A2)
1. Invertendo:
We state the proportion is invertendo if a:b = c:d, which means b:a = d:c.
2. Alternendo:
If a:b = c:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d a:c = b:d
3. Componendo:
We state the proportion is componendo if a:b = c:d a + b:b = c+d:d a + b:b = c+d:d a + b:b = c+d:d a + b:b = c+d:d a + b
4. Dividendo:
If a:b = c:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d a–b:b = c–d:d
5. Componendo and dividendo:
If a:b = c:d
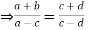The proportion is then said to be in componendo and dividendo.
Q3) State the terms Interest, Rate of interest per annum, Amount, Simple Interest and it’s formula.
A3)
Interest:
The extra money paid by the borrower to the lender on the principal lent is known as interest. The borrower must pay extra money (or interest) for the use of money. I is commonly used to represent interest.
For example:
For a year, Y borrowed 500rs from Z and returned 550rs. In this case, an extra 50 rupees is billed. The interest is 50 rupees.
Rate of interest per annum:
The interest charged annually for every 100rs is referred to as the rate of interest per annum. It is referred to as by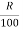 
OR 
.
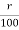Amount:
The total of the principal and interest paid is referred to as the on amount. It is denoted by the letter A.
Simple Interest:
Simple interest is described as interest measured uniformly on the original principal over the loan term. Simple Interest is the symbol for it.
Formula:
Simple interest on the principal "P" lent at a rate of r percent per year for a term of "t" years is normally calculated as follows: S.I =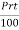 
.
For Example:
Gopi took out a three-year loan from Siva Reddy for 1200 rupees at a rate of 9% per annum.
Sol: P = 1200, r = 9%, t = 3
S.I.=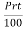
= 1200
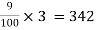rs
Q4) Slove the following questions and calculate the simple intrest,
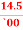
A4)
1) Here p = 1200, I =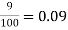 
, n = 3, I = ?
L = p. i.n = 1200 × 0.09 × 3 = 324
Amit will get 324rs as interest.
2) A = P(1+in) = 7500 (1+0.145 × 2.5) = 7500 (1+ 0.3625)
= 7500 × 1.3625 = 10218.75
Reqd. amount = 10218.75
3) Here S.I = 1407, n = 1.5, I = 0.14, P = ?
S.I = P . I.n or , 1407 = p × 0.14 × 1.5
Or, p = 
= 
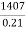= 6700
Required amount = 6700rs
Q5) Peter makes a one-year investment of Rs. 10,000 at a rate of 6% per year. The interest is multiplied every six months. Let's figure out how much interest was received in the first six months .
A5)
I1 = 10,000 x 6/100 x 6/12 = Rs. 300
The principal for the next 6 months = 10,000 + 300 = Rs. 10,300,
so the interest is multiplied.
As a result, I2 = 10,300 x ( 6/100) x 6/12 = Rs. 309
in interest received over the next six months (I2).
As a result,
I = I1 + I2 = 300 + 309 = Rs. 609
is total interest gained during the year.
The interest formula is I = PNR..., where
‘I' stands for interest,
‘P' stands for principal,
‘N' stands for time span, and
‘R' stands for rate of interest.
In this case, R = E, which stands for the effective rate of interest.
As a result, we have
E = I/PN = 609/(10000 1) = 0.0609 (or 6.09%).
Q6) John puts 5,000 rupees into a term deposit scheme. The scheme pays a 6% annual interest rate that is compounded quarterly. After a year, how much interest will John earn? What is the effective rate of interest, as well?
A6) We are aware of this.
● Principal amount = P = Rs. 5,000
● Actual rate of interest = i = 6% p.a. = 0.06 p.a. = 0.015 per quarter
● n = 4 = number of conversion periods (since we are calculating for one year and compounding happens every quarter)
As a result, compound interest (I) is calculated as I = P x [(1 + i)n – 1] = 5000 x [(1 + 0.015)4 – 1] = 5000 x 0.06136355 = 306.82.
As a result, John gains Rs. 306.82 in total interest (I) after a year. E = (1 + i)n – 1 = (1 + 0.015)4 – 1 = 0.0613 or 6.13 percent is also the effective rate of interest (E).
Q7) Solve the following numericals,
i)A credit card's interest rate is quoted as 23 percent p.a. compounded monthly. What is the annual effective interest rate? Make sure your answer is accurate to two decimal points.
ii) If the effective interest rate is 9% a year, the nominal interest rate is compounded quarterly (correct to two decimal places).
A7)
i) Since interest is compounded on a monthly basis, the following equation applies:
Substitute values and solve for i
The effective interest rate is 25,59%25,59% per annum.
ii) Since interest is compounded quarterly, the following is the solution:
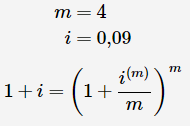
Substitute values and solve for i(m)
The nominal interest rate is 8,71%8,71% p.a. compounded quarterly.
Q8) What is force of interest?
A8)
A nominal interest rate or a discount rate multiplied an infinite number of times (or continuously) per time period is referred to as force of interest.
Consider a nominal interest rate (or even a discount rate) compounded half-yearly, then another compounded quarterly, then another compounded monthly, weekly, regular, compounded every second, and so on, until you can imagine an interest rate compounded every tenth of a second (continuously). The force of interest is the interest rate multiplied over time.
If ip is the annual interest rate multiplied, then the force of interest is the limit of ip as p approaches infinity.
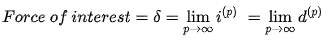
Q9) Solve the following numericals:
i)If the annual effective rate is ten percent per annum, the equivalent force of interest is ten percent per annum.
ii)Take a look at the force of interest obtained in the preceding case. An investor is looking for the appropriate discount rate.
A9)
i)
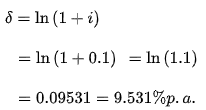
This means that at a rate of interest of 10% p.a. and a force of interest of 9.531 percent p.a., a sum would accumulate to the same value.
ii)
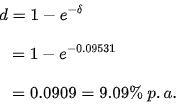
This assumes that a discount rate of 9.09 percent per annum is equivalent to a 10% per annum interest rate or a 9.531 percent per annum force of interest.
Q10) Calculate the cumulative balance after 10 years for the investment strategies in Example 1.7 using a $1,000 principal.
A10)
After ten years, the total amount accrued for Scheme A is
and that for Scheme B is
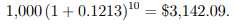
● It's worth noting that the cumulative sum of Scheme B is estimated without using its nominal rate in the preceding example.
● Although i(t) in (1.10) is a one-period effective rate, the definition can be extended to include n-period effective rates.
● The annual effective rate of interest in the period t to t + n is denoted by i(t, t + n), where integral n > 1.
● a(t) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t + n) at time t
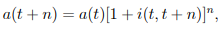…….1.13
which implies
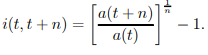……1.14
● The formula (1.10) can also be used for periods of less than a year. Assume that for the duration t to t+t, the effective rate of interest, denoted by i(t, t + t), is defined as
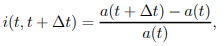…..1.15
which is the effective rate over the time interval t. It's worth noting that this rate isn't annualised.
