Unit – I
Introduction
Q1) Explain types and method of data collection.
A1) Definition:
Data collection is defined as the procedure of collecting, measuring and analyzing accurate insights for research using standard validated techniques.
Irrespective of the field of research, data collection is the primary and most important step for research. Depending on the required information, the approach of data collection is different for different fields of study.
The objective of data collection is ensuring that rich information and reliable data is collected for statistical analysis so that data-driven decisions can be made for research.
Data collection method
Data collection methods can be divided into two categories: secondary methods of data collection and primary methods of data collection.
Secondary data –
Secondary data is a type of data that has already been published in books, newspapers, magazines, journals, online portals etc. there is lot of information available in these sources. Therefore appropriate secondary data are used in the study plays an important role in terms of increasing the levels of research validity and reliability.
Primary data –
Primary data collection methods can be divided into two groups: quantitative and qualitative.
Quantitative data collection methods are based in mathematical calculations in various formats. Methods of quantitative data collection and analysis include questionnaires with closed-ended questions, methods of correlation and regression, mean, mode and median and others. Quantitative methods are less expensive and they can be applied within shorter duration of time. These methods are easy to make comparison between the findings.
Qualitative research methods, on the other hand, do not involve numbers or mathematical calculations. Qualitative research is closely associated with words, sounds, feeling, emotions, colours and other elements that are non-quantifiable.
Primary and secondary data are discussed more in detail in the below section.
Primary data is the information collected through original or first-hand research. Primary data is more reliable and authenticate as the data is nor changed or altered by any human beings. Also, the data is not published yet. Primary data is gathered by any authorized organization, investigator, and enumerator.
“Data which are gathered originally for a certain purpose are known as primary data.” — Horace Secrist.
Sources of primary data
The sources of primary data are as follows –
1. Experiments: In natural sciences, experiments are most reliable source of data collections. Experiments are conducted for medicine, psychological studies, nutrition and other scientific studies. Experiments are conducted in the fields as well as laboratories. The results of experiments are analysed by statistical test and thereafter conclusions are drawn.
2. Survey: surveys are used in social science, management, marketing and psychology to some extent. Surveys are conducted in different methods.
3. Questionnaire: Questionnaires consist of list of question either open ended or close ended for which the participants answer. Questionnaire can be conducted via telephone, mail, institute, fax, etc.
4. Interview: Interviews are expensive method of data collection. The interviewer collects information from each respondent independently. It involves in-depth questioning and follow up question. While taking interview, the interviewer can observe the body language and other reaction to the question.
5. Observation: observation can be conducted with or without knowledge of the participants. Observation can be made either natural or artificially created environment.
Secondary Data:
Secondary data are public information that has been collected by others. The data collected from primary research and used by other is referred as secondary data. The secondary data may be obtained from various sources like industry surveys, database and information system, etc.
“The data which are used in an investigation, but which have been gathered originally by someone else for some other purpose are known as secondary data.” — Blair
Sources of secondary data-
2. Books – books are available on any topic you want to research. Books provide insight on how much information is given for a particular topic and you can prepare your literature review.
3. Journals – journals provide up to date information on the very specific topic on which you want to research. Journal is one of the most important sources for providing the information on data collected.
4. Magazine or newspaper – Newspaper or magazine provide daily information regarding politics, business, sports, fashion, etc which can be used for conducting research.
5. Internet – internet is becoming advance, fast and reachable to the masses and much information is available on internet. Almost all journals, books are available on internet. Some are free and others you have to pay price
6. Company website – company’s website provides lots of information. They have a section called investor relations which contains full of annual reports, regulatory findings and investor presentations that can provide insights into both the individual company’s performance and that of the industry at large.
Q2) Explain scope, importance and limitation of statistics.
A2) The word statistics is derived from the Latin word “Status” that means a group of numbers that represent some information of our human interest. In ancient periods, the use of statistics was made to meet the administrative needs of the state. In modern time, the statistics is not only used for administrative of the state alone, also evaluate all those activities in our lives which can be expressed in quantitative terms.
The term “statistics” is defined in two senses: - in singular and in Plural senses.
Firstly in plural sense, statistics means systematic collection of numerical facts. Secondly in singular sense, the term statistics means the various methods used for collection, analysis and interpretation of numerical facts. It is described as statistical method. In our study we are more concerned with the second meaning of statistics.
Definition:
“Statistics is a body of methods for making wise decisions on the face of uncertainty.” —Wallis and Roberts
“Statistics is a body of methods for obtaining and analyzing numerical data in order to make better decisions in an uncertain world.” —Edward N. Dubois
Statistics are numerical statement of facts in any department of enquiry placed interrelation to each other.- Bouly.
The science of Statistics is essentially a branch of applied mathematics and can be regarded as a mathematics applied to observation data.- R.A fisher.
After analyzing the various definitions of statistics, the most proper definition of statistics are as follows
“Statistics in the plural sense are numerical statements of facts capable of some meaningful analysis and interpretation, and in singular sense, it relates to the collection, classification, presentation and interpretation of numerical data.”
Scope of statistics

Functions of statistics
2. Presentation of facts – Statistics helps in presenting the complex data in a simple form, so that it becomes easy to understand. Statistical methods present data in the form of graph, diagram, average, coefficient, etc.
3. Comparison – After simplifying the data, it can be correlated and compared. Comparing data relating to fact is one of the functions of statistics as absolute figures convey less meaning.
4. It helps other science- Many laws of economic, law of demand, law of supply have been verified with the help of statistics.
5. Forecasting – Statistics also predicts future course of action. On the basis of estimates with the help of statistics we can make future policies.
6. Policy making – Statistics helps in formulating favorable policies. Based on the forecast the government makes policies.
Uses and importance of statistics
2. Importance for businessman – statistics helps in providing relevant data. Thus with the help of those data a business man can estimate demand and supply of the commodity.
3. Importance in economics – statistics helps in measuring economics such as gross national output, consumption, saving, investment, expenditures, etc
4. Importance for politician – Politician use statistics in formulating economic, social and educational policies of the country
5. Importance in the field of education – statistics has wide application in education for determining the reliability and viability to a test, factor analysis, etc.
Limitation of statistics:
2. Study of aggregates only – statistics study only aggregates of quantitative facts. It does not study any particular unit. Prof. Horace Sacrist defined statistics, “By statistics we mean aggregates of facts…. and placed in relation to each other”
3. It does not depict the entire story of phenomena – Any phenomena happen, due to many causes. But all the cause is not expressed in numbers. So, correct conclusion cannot be drawn. Analyzing quantitative data and ignoring qualitative data cannot give 100% conclusion.
4. Homogeneity of data – To compare the data, it is essential that whatever statistics are collected, the same must be uniform in quality.
5. It is liable to be miscued – As W.I. King points out, “One of the short-comings of statistics is that do not bear on their face the label of their quality.” Thus the data collected by inexperienced person may be dishonest or biased. So to get correct conclusion data must be used in caution.
6. Too many methods to study a problem –to find a single result many statistical methods are used. All the methods result vary in each case. “It must not be assumed that the statistics is the only method to use in research, neither should this method of considered the best attack for the problem.” —Croxten and Cowden.
Q3) The following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
A3)
Income | No. of families | Xm (Mid point) | fXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |

X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Q4) Calculate the harmonic mean for the below data
Marks | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
F | 2 | 3 | 11 | 20 | 32 | 25 | 7 |
A4)
Marks | X | F | F/X |
30-39 | 34.5 | 2 | 0.0580 |
40-49 | 44.5 | 3 | 0.0674 |
50-59 | 54.4 | 11 | 0.2018 |
60-69 | 64.5 | 20 | 0.3101 |
70-79 | 74.5 | 32 | 0.4295 |
80-89 | 84.5 | 25 | 0.2959 |
90-99 | 94.5 | 7 | 0.0741 |
Total |
| 100 | 1.4368 |
HM = 100/1.4368 = 69.59
Q5) Calculate the geometric mean.
X | F |
60 – 80 | 22 |
80 – 100 | 38 |
100 – 120 | 45 |
120 – 140 | 35 |
|
|
A5)
X | f | Mid X | Log X | f log X |
60 – 80 | 22 | 70 | 1.845 | 40.59 |
80 – 100 | 38 | 90 | 1.954 | 74.25 |
100 – 120 | 45 | 110 | 2.041 | 91.85 |
120 – 140 | 35 | 130 | 2.114 | 73.99 |
Total | 140 |
|
| 280.68 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 280.68/140
= antilog 2.00
GM = 100
Q6) Calculate the median
Marks | No. of students |
0-4 | 2 |
5-9 | 8 |
10-14 | 14 |
15-19 | 17 |
20-24 | 9 |
A6)
Marks | No. of students | CF |
0-4 | 2 | 2 |
5-9 | 8 | 10 |
10-14 | 14 | 24 |
15-19 | 17 | 41 |
20-24 | 9 | 50 |
| 50 |
|
n = 50
 n = 50/2= 25
n = 50/2= 25
2
The category containing n/2 is 15 -19
Lb = 15
Cfp = 24
f = 17
ci = 4



 Median = 15 + 25-24 *4 = 15.23
Median = 15 + 25-24 *4 = 15.23
17
Q7) In a class of 30 students marks obtained by students in science out of 50 is tabulated below. Calculate the mode of the given data.
Marks obtained | No. of students |
10 -20 | 5 |
20 – 30 | 12 |
30 – 40 | 8 |
40 – 50 | 5 |
A7)
The group with the highest frequency is the modal group: - 20 -30
D1 = 12 - 5 = 7
D2 = 12 - 8 = 4
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
7+4
Mode = 61.8
Q8) Calculate Q1, Q2 and Q3 from the following data given below:
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
A8)
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:

Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
Q9) Calculate mean deviation from the median
Class | 5 -15 | 15 – 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
A9)
x | f | cf | Mid-point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 
 Median = 25+16-14 *10 = 27.42
Median = 25+16-14 *10 = 27.42
7
MD from median is 390. 32/32 = 12.91
Q10) Calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
A10)
Class interval | Frequency | Mid point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |

Mean = 2720/40 = 68
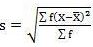
SD = √10510/40 = 16.20


