Unit – III

Probability

Q1) From a pack of 52 cards, two cards are drawn at random one after the other with replacement. What is the probability that both cards are kings?

A1)

 The probability of drawing a king P (A) =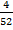 

The probability of drawing again the king after replacement P (B) =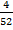 

Since the two events are independent, the probability of drawing two kings is:

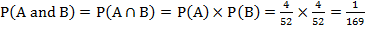
Q2) A bag contains 4 red balls, 3 white balls and 5 black balls. Two balls are drawn one after the other with replacement. Find the probability that first is red and the second is black.

A2)

 Probability of red ball in the first draw = 

 The probability of a black ball in the second draw = 

Since the events are independent, the probability that first is red and the second are black will be:

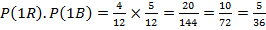
Q3) A bag contains 5 white and 3 red balls and four balls are successively drawn and are not replaced. What is the chance that (i) white and red balls appear alternatively and (ii) red and white balls appear alternatively?

A3)

(i) The probability of drawing a white ball = 5/8

The probability of drawing a red ball = 3/7

The probability of drawing a white ball = 4/6 and the probability of drawing a red ball = 2/5

Since the events are dependent, therefore the required probability is:

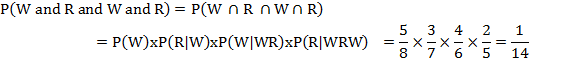
(ii) The probability of drawing a red ball = 3/8 and the probability of drawing a white ball = 5/7

The probability of drawing a red ball = 2/6 and the probability of drawing a white ball = 4/5

Since the events are dependent, therefore the required probability is:

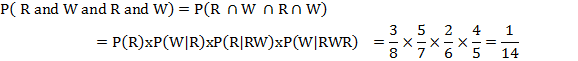
Q4) Find the number of permutations and combinations if n = 12 and r = 2.

A4)

Given,

n = 12

r = 2

Using the formula given above:

Permutation:

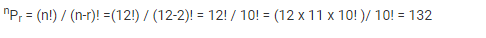
Combination:

Q5) I roll a fair die twice and obtain two numbers  X1= result of the first roll and X2= result of the second roll. Given that I know X1+X2=7, what is the probability that X1=4 or X2=4?

A5)

Q6) I roll a fair die. Let A be the event that the outcome is an odd number, i.e., A={1,3,5}. Also let B be the event that the outcome is less than or equal to 3, i.e., B={1,2,3}. What is the probability of A, P(A)? What is the probability of A given B, P(A|B)?

A6)

This is a finite sample space, so

P(A)=|A|/|S|=|{1,3,5}|/6=12.

Now, let's find the conditional probability of A given that B occurred. If we know B has occurred, the outcome must be among {1,2,3}. For A to also happen the outcome must be in A∩B={1,3}. Since all die rolls are equally likely, we argue that P(A|B) must be equal to

P(A|B)=|A∩B|/|B|=23.

Q7) Ten coins are tossed simultaneously. Find the probability of getting (i) atleast seven heads (ii) exactly seven heads (iii) atmost seven heads

A7)

p = Probability of getting a head = ½ 2

q = Probability of not getting a head =1/2

The probability of getting x heads throwing 10 coins simultaneously is given by

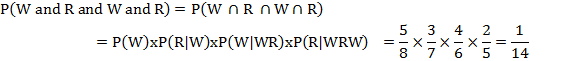
Q8) If 2% of electric bulbs manufactured by a certain company are defective. Find the probability that in a sample of 200 bulbs i) less than 2 bulbs ii) more than 3 bulbs are defective.[e-4 = 0.0183]

A8)

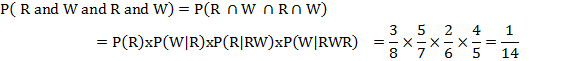
Q9) In a normal distribution whose mean is 12 and standard deviation is 2. Find the probability for the interval from x = 9.6 to x = 13.8.

A9)

Q10) For a normal distribution whose mean is 2 and standard deviation 3. Find the value of the variate such that the probability of the variate from the mean to the value is 0.4115.

A10)