Q1) Explain concepts of cost? (8 marks)

A1)

Concept of cost

A firm who wants to maximize their profit concentrates on revenue and cost of the firm. Profit of the firm can be increased either by increasing revenue or by reducing cost. Firm generally cannot influence revenue because it is determined by the market forces but it is possible for the firm to reduce cost by producing maximum output or by increasing efficiency of the organization.

For managerial decision-making, cost is very important because it helps to decide price for the commodity. It also helps to decide whether to increase the production or not. Therefore, understanding of cost concepts is very important.

Social cost on the other hand is bared by the society as a result of production of commodity. Even though social cost occurs due to production of a commodity it is not bared by the producer. It consists of external cost. E.g.: If a factory is located in a residential area causes air pollution. Due to pollution as the health of the people living in that area affects, they have to spend money on medical facilities. Even though this cost occurs due to the factory, it is passed on to the society at large. Externalities are included in the social cost

b.  Historical cost and Replacement cost: The original money value spent at the time of purchasing of an asset is called historical cost. Most of the assets in the balance sheet are at the historical cost. One of the advantages of historical cost is that records maintained on the basis of historical cost are considered to be reliable, consistent, comparable and verifiable. Historical cost does not reflect current market valuation.

The amount which has to be spent at the time of replacing of the existing asset is called the replacement cost. This cost reflects the current market prices. If we consider an increase in prices over the years, replacement cost will be greater than historical cost. If we consider fall in prices over the years, replacement cost will be less than historical cost and if we consider prices to be constant over the years, replacement cost and historical costs are the same.

c.   Fixed cost and Variable cost: Fixed cost refers to the firm’s expenditure on fixed factors of production. Even if no output is produced, fixed cost needs to be paid. Even if output increases in the short run, fixed cost remains constant. E.g.: If a businessman borrows money from a bank to start his business. Initially even if his output is zero, he has to pay the interest on borrowed capital. Rent on land, insurance premium, tax payment are some of the examples of fixed cost. Addition of all fixed cost gives Total Fixed Cost.

Variable cost on the other hand refers to the firm’s expenditure on variable factors of production. When no output is produced, variable cost is zero. As output increases, variable cost also increases. Payment for raw material, wages and salaries of the workers are some of the examples of variable cost. Addition of all variable costs gives the Total Variable Cost.

d.  Total cost, Average cost and Marginal cost: Total cost (TC) – Firms total expenditure on all fixed and variable factors for producing a commodity is called the Total cost of production. Therefore TC= TFC+TVC For zero level of output there is some total cost. It increases with an increase in the level of output

Average Cost (AC) or Average Total Cost (ATC) – It refers to the per unit cost of producing a commodity. It is calculated by the following formula

AC = TC/Q

Where AC = Average cost TC = Total cost Q = Number of units produced

Average cost can also be calculated by using following formula

AC or ATC = AFC+AVC

Where AC- Average Cost AFC- Average Fixed Cost AVC- Average Variable Cost

Average Fixed Cost (AFC)- It is the per unit fixed cost of production. It can be calculated by the following formula

AFC= TFC/Q

Where TFC= Total Fixed Cost Q = Number of units produced

Average Variable Cost (AVC) - It is the per unit variable cost of production. It can be calculated by the following formula

AVC= TVC/Q

Where TVC= Total Variable Cost Q= Number of units produced

Marginal Cost (MC) - It is the addition made to the total cost. Or cost of producing an additional unit of output is called as the marginal cost. It can be calculated by using following formula

MC = Change in total cost/ change in output TC

Eg: If total cost of producing 2 cars is Rs. 3, 00,000 and the total cost of producing 3 cars is Rs. 4, 50,000. Then the marginal cost is Rs. 1, 50,000 i.e. the cost of producing an additional unit of output.

e.   Sunk Cost and Incremental Cost: In order to enter in to the market certain costs are incurred by the firm. These costs are known as Sunk cost. It includes the cost by the firm for setting up the business, advertisement etc. These costs cannot be recovered by the firm if they decide to exit the market.

Incremental cost refers to a change in total coat as a result of policy change or a change in managerial decision. The concept of incremental cost is broader as compared to marginal cost.

Marginal cost considers a change in total cost due to a unit change in output whereas incremental cost considers a change in total cost due to an introduction of new product, change in advertising strategy, additional batch of output etc. The concept of incremental cost is more relevant as compared to marginal cost because the firm increases its output in batches and not by unit only.

f.     Implicit Cost and Explicit Cost: Implicit cost refers to the cost of all own factors which the entrepreneur employs in the business. It includes salary and wages for the service of entrepreneur, interest on capital invested by the entrepreneur etc. Implicit costs are also called indirect cost because direct cash payment is not made to own factors of production.

If entrepreneur sold these services to others, he would have earned money. Therefore, implicit cost is also the opportunity cost of factors owned by him.

Explicit cost on the other hand is the direct cash payment made by the firm for purchasing or hiring of various factors of production. E.g. Rent paid for hiring of land, money spent for purchasing for raw material, wages and salaries paid to the employees, expenditure on transport, power, advertising etc.

g.  Accounting and Economic Cost: Accounting cost includes only explicit cost i.e. the firm’s expenditure on purchasing of various factors of production. For financial purpose and tax purpose, accounting cost is important.

Economic cost on the other hand includes both explicit and implicit cost. This cost is important for managerial decision making. Therefore an economist who wants to take any decision considers both explicit and implicit cost.

Q2) Explain total cost, marginal cost and average cost? (5 marks)

A2)

Average Cost (AC) or Average Total Cost (ATC) – It refers to the per unit cost of producing a commodity. It is calculated by the following formula

AC = TC/Q

Where AC = Average cost TC = Total cost Q = Number of units produced

Average cost can also be calculated by using following formula

AC or ATC = AFC+AVC

Where AC- Average Cost AFC- Average Fixed Cost AVC- Average Variable Cost

Average Fixed Cost (AFC)- It is the per unit fixed cost of production. It can be calculated by the following formula

AFC= TFC/Q

Where TFC= Total Fixed Cost Q = Number of units produced

Average Variable Cost (AVC) - It is the per unit variable cost of production. It can be calculated by the following formula

AVC= TVC/Q

Where TVC= Total Variable Cost Q= Number of units produced

Marginal Cost (MC) - It is the addition made to the total cost. Or cost of producing an additional unit of output is called as the marginal cost. It can be calculated by using following formula

MC = Change in total cost/ change in output TC

Eg: If total cost of producing 2 cars is Rs. 3, 00,000 and the total cost of producing 3 cars is Rs. 4, 50,000. Then the marginal cost is Rs. 1, 50,000 i.e. the cost of producing an additional unit of output.

Q3) What do you mean by Learning Curve? (5 marks)

A3)

The learning curve shows an inverse relationship between an average cost of production and the level of output. This means that as firm produces more and more output, its average cost of production declines. Therefore, the learning curve slopes downward from left to right. Following diagram explains the learning curve effect.

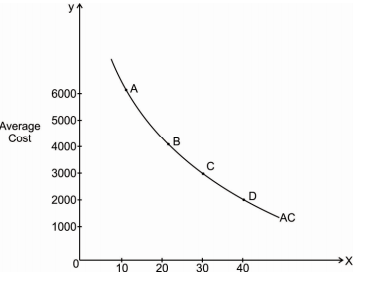
In the above diagram X axis represents total output and Y axis represents the average cost. It shows that average cost is RS.6000 for producing 10 units of output. As output increases to 20, 30 and 40 units, average cost declines to 4000, rs 3000 and rs 2000 respectively. Points P, Q, R and S shows different combinations of output and average cost.

Learning curve effect is a result of an experience which the firm gains during the process of production. When the firm is new, it takes time for the firm to produce the output. Thus, the costs are high. As firm becomes older, it learns to use new techniques of production, efficient way of using raw material and skills. Workers also become efficient over a period of time. All this will help to reduce the average cost of production. Firm learn to reduce cost through experience. Therefore, learning curve is also called an Experience curve. The effect of learning curve applies to the manufacturing and service sector.

As shown in the diagram learning curve initially declines faster and then declines at a slower rate. This means that when the production process is new, average cost declines much faster as compared to the old production process

Q4) Explain the following concepts a) Implicit cost and Explicit cost b) Private cost and Social cost c) Historical cost and Replacement cost d) Total cost, Average cost and Marginal cost e) Fixed cost and Variable cost f) Opportunity cost. (8 marks)

A4)

Implicit cost refers to the cost of all own factors which the entrepreneur employs in the business. It includes salary and wages for the service of entrepreneur, interest on capital invested by the entrepreneur etc. Implicit costs are also called indirect cost because direct cash payment is not made to own factors of production. If entrepreneur sold these services to others, he would have earned money. Therefore, implicit cost is also the opportunity cost of factors owned by him. Explicit cost on the other hand is the direct cash payment made by the firm for purchasing or hiring of various factors of production. E.g. Rent paid for hiring of land, money spent for purchasing for raw material, wages and salaries paid to the employees, expenditure on transport, power, advertising etc.

b.  Private cost and Social cost

Costs which are directly incurred by the individual or firm producing good or service is called private cost. This cost gives private benefit to an individual or firm engaged in relevant activity. Some of the examples of private cost are firm’s expenditure on purchase of raw material, payment of rent, wages and salaries, interest, insurance, depreciation etc. Similarly company’s expenditure for its labor, advertising cost for the promotion of  goods, transportation cost to carry goods from company to the market are also considered as private cost.

Social cost on the other hand is bared by the society as a result of production of commodity. Even though social cost occurs due to production of a commodity it is not bared by the producer. It consists of external cost. E.g.: If a factory is located in a residential area causes air pollution. Due to pollution as the health of the people living in that area affects, they have to spend money on medical facilities. Even though this cost occurs due to the factory, it is passed on to the society at large. Externalities are included in the social cost.

c.   Historical cost and Replacement cost

The original money value spent at the time of purchasing of an asset is called historical cost. Most of the assets in the balance sheet are at the historical cost. One of the advantages of historical cost is that records maintained on the basis of historical cost are considered to be reliable, consistent, comparable and verifiable. Historical cost does not reflect current market valuation.

The amount which has to be spent at the time of replacing of the existing asset is called the replacement cost. This cost reflects the current market prices. If we consider an increase in prices over the years, replacement cost will be greater than historical cost. If we consider fall in prices over the years, replacement cost will be less than historical cost and if we consider prices to be constant over the years, replacement cost and historical costs are the same.

d.  Total cost, Average cost and Marginal cost

Firms total expenditure on all fixed and variable factors for producing a commodity is called the Total cost of production. Therefore TC= TFC+TVC For zero level of output there is some total cost. It increases with an increase in the level of output.

Average Cost (AC) or Average Total Cost (ATC) – It refers to the per unit cost of producing a commodity. It is calculated by the following formula

AC = TC/Q

Where AC = Average cost TC = Total cost Q = Number of units produced

Average cost can also be calculated by using following formula

AC or ATC = AFC+AVC

Where AC- Average Cost AFC- Average Fixed Cost AVC- Average Variable Cost

Average Fixed Cost (AFC)- It is the per unit fixed cost of production. It can be calculated by the following formula

AFC= TFC/Q

Where TFC= Total Fixed Cost Q = Number of units produced

Average Variable Cost (AVC) - It is the per unit variable cost of production. It can be calculated by the following formula

AVC= TVC/Q

Where TVC= Total Variable Cost Q= Number of units produced

Marginal Cost (MC) - It is the addition made to the total cost. Or cost of producing an additional unit of output is called as the marginal cost. It can be calculated by using following formula

MC = Change in total cost/ change in output TC

Eg: If total cost of producing 2 cars is Rs. 3, 00,000 and the total cost of producing 3 cars is Rs. 4, 50,000. Then the marginal cost is Rs. 1, 50,000 i.e. the cost of producing an additional unit of output.

e.   Fixed cost and Variable cost

Fixed cost refers to the firm’s expenditure on fixed factors of production. Even if no output is produced, fixed cost needs to be paid. Even if output increases in the short run, fixed cost remains constant. E.g.: If a businessman borrows money from a bank to start his business. Initially even if his output is zero, he has to pay the interest on borrowed capital. Rent on land, insurance premium, tax payment are some of the examples of fixed cost. Addition of all fixed cost gives Total Fixed Cost.

Variable cost on the other hand refers to the firm’s expenditure on variable factors of production. When no output is produced, variable cost is zero. As output increases, variable cost also increases. Payment for raw material, wages and salaries of the workers are some of the examples of variable cost. Addition of all variable costs gives the Total Variable Cost.

f.     Historical cost and Replacement cost:

The original money value spent at the time of purchasing of an asset is called historical cost. Most of the assets in the balance sheet are at the historical cost. One of the advantages of historical cost is that records maintained on the basis of historical cost are considered to be reliable, consistent, comparable and verifiable. Historical cost does not reflect current market valuation.

The amount which has to be spent at the time of replacing of the existing asset is called the replacement cost. This cost reflects the current market prices. If we consider an increase in prices over the years, replacement cost will be greater than historical cost. If we consider fall in prices over the years, replacement cost will be less than historical cost and if we consider prices to be constant over the years, replacement cost and historical costs are the same

Q5) Explain the relationship between TFC, TVC and TC with the help of diagram. (5 marks)

A5)

Relationship between TFC, TVC and TC in the short run TFC is the firm’s total expenditure on fixed factors of production. For zero level of output TFC is zero. It remains constant for all the levels of output.

TVC on the other hand is the firm’s total expenditure on variable factors of production. For zero level output TVC is zero. It increases with an increase in the level of output.

Total cost is the additional of Total Fixed Cost and Total Variable Cost. In the following table relationship between TFC, TVC and TC is discussed for different units of output

Explanation – In table First column shows various levels of output starting from zero units to 8 units. Second column shows TFC. As fixed factors of production are constant for certain level of output TFC is also constant for all level of output. For zero level of output also TFC is Rs. 50. Third column shows TVC which is zero for zero level of output. With an increase level of output TVC initially increases at decreasing rate then increases at an increasing rate. This is because of the law of variable proportions. Forth column shows TC which is the addition of TFC and TVC. TC increases with an increase level in the output. TC increases in the same proportions as increased in TVC.

This relation between TFC, TVC and TC can be explained with the help of following diagram.

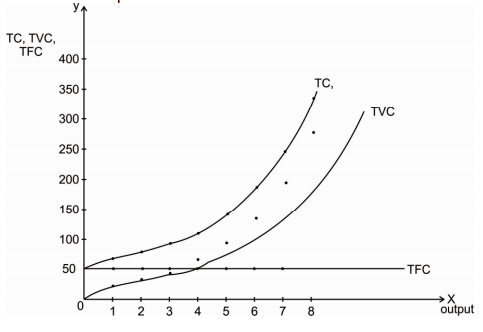
By plotting different combinations of output and TFC, TVC and TC, we have TFC curve, TVC curve and TC curves.

Diagram shows that TFC curve is a straight-line curve parallel to X axis. This is because when output is zero, some fixed cost has to be paid and this cost remains constant for all the levels of output. TFC curve is horizontal.

TVC curve starts at the point of origin because when output is zero, TVC is also zero. TVC curve initially increases at a diminishing rate with an increase in the level of output and then increases at an increasing rate.

As TC is the addition of TFC and TVC, TC curve is above TFC and TVC curves. The shape of TC curve is same as the TVC curve. The gap between TC and TVC curve measures TFC.

Q6) Explain the derivation of Long run Average Cost curve? (5 marks)

A6)

Different plant sizes are available to the firm to operate in the long run. For a specific level of output, the plant of specific size is more suitable. For every size of plant there will be a specific average cost and thus a specific average cost curve. In the long run different short run average cost curves are available for different sizes of plant. The firm has to choose the specific size of plant for its operation.

Derivation of Long run average cost curve with a number of short run average cost curves can be discussed with the help of following diagrams

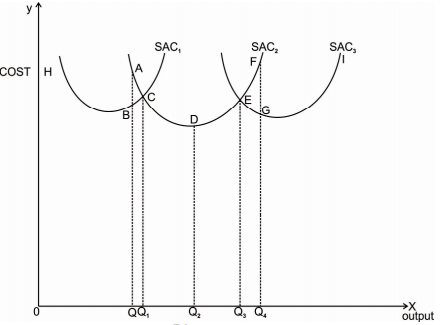
Here we assume that there are three sizes of plant.

Above figure shows that there are three plants available to the firm and are shown by three different cost curves- SAC1, SAC2 and SAC3. For a particular level of output, a specific plant is most suited.

Above diagram shows that for producing OQ level of output on plant SAC1, cost is BQ and on plant SAC2 cost is AQ. This shows that OQ level of output can be produced with lower cost QB with SAC1 as compared to plant SAC2.

If the firm wants to produce OQ1 level of output, it can be produced either with plant SAC1 or SAC2. But it is better for the firm to go with plant SAC2 because as shown in the diagram higher level of output OQ2 can be produced with much lower cost on SAC2. With plant SAC2, output greater than OQ1 and less than OQ3 can be produced at lower average cost.

For output greater than OQ3 firm will use plant SAC3 because the average cost with SAC2 will be greater as compared to average cost with SAC3.

Derivation of LAC

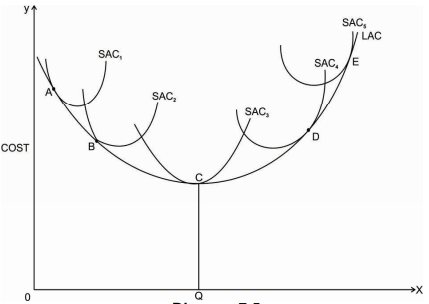
From the above explanation it is clear that in the long run the firm has alternative plant sizes available for the production and the firm will choose that plant size which gives minimum average cost for producing a given level of output. Accordingly to the first figure with three short run average cost curves the Long run Average Cost curve is HBCEGI.

If we assume that there are infinite plant sizes available, there are number of short run average cost curves corresponding to each plant size. Therefore, the LAC will be a smooth U-shaped curve as shown in second diagram above.

As LAC curve is a locus of points of the lowest average cost of producing different levels of output. Every point of LAC will have a tangency point with SAC curve. It can be seen from the above diagram that LAC curve is tangent to the minimum point of SAC3 curve only at the optimum level of output OQ. Plant SAC3 is considered as the optimum size of plant because it produces optimum level of output OQ with minimum cost CQ.

For any output less than OQ, LAC curve is tangent to SAC curve on its declining part ie. At point A and B on SAC1 and SAC2. For any output greater than OQ, LAC curve is tangent to SAC curve on its increasing part i.e. At point D and E on SAC4 and SAC5.

It can be seen from second Diagram that LAC curve initially declines, reaches to minimum and again increases with an increase in the level of output. LAC curve is much flatter than SAC curves. LAC curve declines due to economies of scale and increases due to diseconomies of scale.

As the LAC curve includes the family of short run average cost curves, it is called an Envelop curve. In the long run firm can also plan to increase its scale of production and therefore LAC curve is also called the Planning Curve.

Q7) Discuss the Learning curve effect? (5 marks)

A7)

The learning curve shows an inverse relationship between an average cost of production and the level of output. This means that as firm produces more and more output, its average cost of production declines. Therefore, the learning curve slopes downward from left to right. Following diagram explains the learning curve effect.

In the above diagram X axis represents total output and Y axis represents the average cost. It shows that average cost is RS.6000 for producing 10 units of output. As output increases to 20, 30 and 40 units, average cost declines to 4000, rs 3000 and rs 2000 respectively. Points P, Q, R and S shows different combinations of output and average cost.

Learning curve effect is a result of an experience which the firm gains during the process of production. When the firm is new, it takes time for the firm to produce the output. Thus, the costs are high. As firm becomes older, it learns to use new techniques of production, efficient way of using raw material and skills. Workers also become efficient over a period of time. All this will help to reduce the average cost of production. Firm learn to reduce cost through experience. Therefore, learning curve is also called an Experience curve. The effect of learning curve applies to the manufacturing and service sector.

As shown in the diagram learning curve initially declines faster and then declines at a slower rate. This means that when the production process is new, average cost declines much faster as compared to the old production process

Q8) Bring out the relationship between AC and MC? (5 marks)

A8)

AC is the per unit cost of production and marginal cost is the cost of producing an additional unit of output. Relationship between AC and MC can be discussed with the help of following diagram.

For initial levels of output AC and MC both curves are declining, but MC is less than AC. When MC is less than AC it means that cost of producing an additional unit of output is less than per unit cost of production. As MC

At a certain level of output (optimum level of output) AC is minimum. At this point MC curve intersects AC curve. Thus AC=MC. It means that cost of producing an additional unit of output is exactly equal to the average cost of production. As AC=MC, new AC must be equal to the old average cost.

At higher levels of output AC and MC both are increasing but MC>AC. It means that the cost of producing an additional unit of output is greater than the average cost of production. As MC>AC, new average cost must be greater than old average cost. Therefore, AC curve is rising. From the above explanation we can conclude that when

MC<AC, MC pulls the AC curve down

MC=AC, AC curve is flat as MC pulls AC horizontally.

MC>AC, MC pulls the AC curve up.

Long run cost and output relationship

As the name suggests long run refers to a sufficiently long period. As the long period is available, firm can make necessary change in all factors of production as per the changes in demand. Thus, in long run all factors of production are variable. Hence there are no fixed cost in the long run. Depending on the type of industry the length of long run can differ. For a firm producing a particular product, long run may be years

In the long run firm can make proper planning and build that size of plant which will minimize the cost of production for producing optimum level of output. Once the particular plant has been built, the firm operates in the short run. This means that even though firm operates in the short run, it plans in the long run.

Q9) Define AC,AFC, AVC and MC and also discuss the relationship between them. (8 marks)

A9)

Production function gives the functional relationship between the level of output and the various factor inputs (land, labor, capital and entrepreneur). The cost of production depends on the level of output produced, nature of technology used, prices of factors of production. Thus, the cost function is derived from the production function. The cost function is given as

C = f (Q, T, Pf)

Where C = total cost Q = Level of output produced T = Technology Pf = Prices of factors f = Functional relationship

If we assume that technology, prices of factors are constant, total cost increases with an increase in the level of output i.e. C = f(Q).

Any change in production function will shift cost function either up or down. E.g. Use of better techniques of production, use of better-quality raw material, use of efficient labors etc. will improve the production function and thus reduce the cost function. Similarly use of poor-quality raw material, inefficient techniques of production, unskilled labor will shift the production function up.

The relationship between cost and output needs to be studied in the short run and in the long run.

Short run cost output relationship

As the name suggests short run is a very short period where the firm produces its output by changing only variable factors of production. This is because in the short run fixed factors of production remain constant for all the levels of output. Following table shows the behavior of output and various costs in the short run.

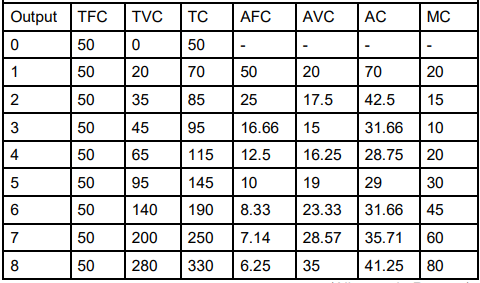
In the above table output is shown in the (1st) column, which increases from 0 units to 8units. For all the levels of output TFC in column (2) remain constant i.e. Rs. 50. TVC in the (3rd) column is zero for zero level of output. And then increases with an increase in the level of output. In column (4) TC is calculated by adding TFC and TVC

AFC in column (5) is calculated by using the formula TFC/Q. As TFC remain constant for all the levels of output, AFC continuously declines with an increase in the level of output.

AVC in column (6) is calculated by using formula TVC/Q. Initially AVC declines. At third level of output it reaches to the minimum and then increases with an increase with an increase in the level of output.

AC in column (7) is calculated by using the formula TC/Q. AC also declines initially reaches to the minimum point at 4th unit of output and then increases with an increase in the level of output.

MC in column (8) is the cost of producing an additional unit of output. It is calculated by the formula 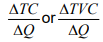. This is because TC increases by the same amount as increase in TVC. MC initially declines, reaches to minimum and increases thereafter.

Diagrammatic relationship between AFC, AVC, AC and MC is as follows-

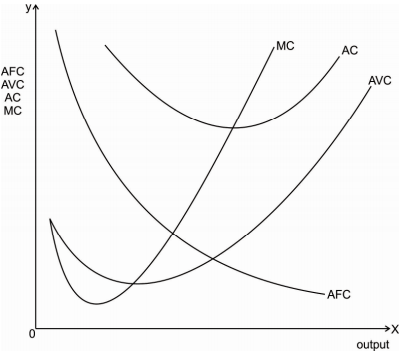
Explanation:

1. As AFC is continuously declining. AFC curve slopes downward from left to right.

2. Initially AVC curve is declining, reaches to a minimum and then increases with an increase in the level of output. AVC curve starts increasing after a normal capacity level of output is produced. More intensive use of various factors of production leads to an increase in AVC.

3. AC curve lies above AFC and AVC curves because AC is the addition of AFC and AVC. AC curve initially declines due to fall in AFC curve. AC curve reaches to minimum point and then increases due to an increase in AVC curve. AC curve is a Ushaped curve.

4. MC curve is also a U-shaped curve. MC curve also falls in the beginning, reaches to the minimum and then increases. When MC curve starts rising, it intersects the AVC curve and AC curve at their minimum point.

Relationship between AC and MC:

AC is the per unit cost of production and marginal cost is the cost of producing an additional unit of output. Relationship between AC and MC can be discussed with the help of following diagram.

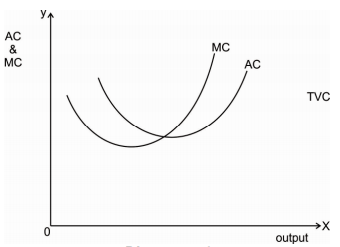
For initial levels of output AC and MC both curves are declining, but MC is less than AC. When MC is less than AC it means that cost of producing an additional unit of output is less than per unit cost of production. As MC

At a certain level of output (optimum level of output) AC is minimum. At this point MC curve intersects AC curve. Thus AC=MC. It means that cost of producing an additional unit of output is exactly equal to the average cost of production. As AC=MC, new AC must be equal to the old average cost.

At higher levels of output AC and MC both are increasing but MC>AC. It means that the cost of producing an additional unit of output is greater than the average cost of production. As MC>AC, new average cost must be greater than old average cost. Therefore, AC curve is rising. From the above explanation we can conclude that when

MC<AC, MC pulls the AC curve down.

MC=AC, AC curve is flat as MC pulls AC horizontally.

MC>AC, MC pulls the AC curve up.

Long run cost and output relationship

As the name suggests long run refers to a sufficiently long period. As the long period is available, firm can make necessary change in all factors of production as per the changes in demand. Thus, in long run all factors of production are variable. Hence there are no fixed cost in the long run. Depending on the type of industry the length of long run can differ. For a firm producing a particular product, long run may be years

In the long run firm can make proper planning and build that size of plant which will minimize the cost of production for producing optimum level of output. Once the particular plant has been built, the firm operates in the short run. This means that even though firm operates in the short run, it plans in the long run.

Q10) Explain the concept of break-even point with the help of diagram. (5 marks)

A10)

Break-even analysis studies the relationship between total cost, total revenue, total profits and losses over a range of output. Break-even point is a point where the total revenue of the firm is equal to total cost. Therefore, at break-even point there is no profit, no loss.

Break-even analysis technique is used in the business to determine the level of production or sales volume which is necessary for the business to cover its cost of doing a business. In financial analysis the concept of break-even point is most commonly used. The concept of break-even point can be explained with the help of following table

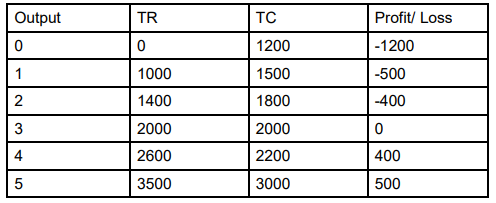
Above table shows that break-even level of output is 3 units because, firms TR and TC are equal at 3 units of output and therefore there is no profit, no loss.

Break-even point can also be explained with the help of following diagram

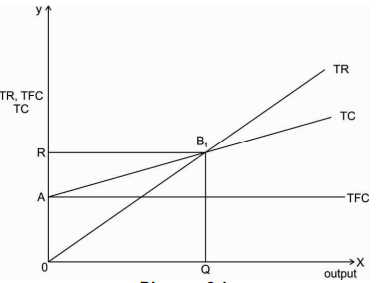
Above diagram is drawn on the basis of the assumption that TR and TC curves are linear i.e. TR and TC increases at a constant rate with an increase in the level of output. Therefore, TR and TC curves are straight lines.

For initial levels of output total cost is greater than total revenue therefore the firm is making loss. At output OQ, firm stops making loss, TR=TC therefore there is no profit no loss. Thus, OQ is the break-even output and B1 is the break-even point. After OQ level of output total revenue is greater than total cost and thus firm starts making profit.

When TR and TC curves are linear, there is only one breakeven point. According to above diagram entire output after breakeven output gives profit. However, this may not be true because of changes in price and cost.

If we do not consider constant change in TR and TC, TR and TC curves are non-linear. In this case we have more than one break-even point as shown in the following diagram

In the above diagram on the Y axis we measure cost and revenue and on the X axis we measure output.

In case of non-linear TR and TC curves there two breakeven points P and Q, indicating lower level of output OM and higher level of output ON respectively. For any output less than OM and greater than ON, firm makes losses because TC>TR. Between the range of output M and N, TR>TC and thus firm makes profit.

Q11) Discuss the implications and limitations of break-even analysis. (5 marks)

A11)

Break-even analysis studies the relationship between total cost, total revenue, total profits and losses over a range of output. Break-even point is a point where the total revenue of the firm is equal to total cost. Therefore, at break-even point there is no profit, no loss.

Application of breakeven analysis

Business firms are interested in understanding break-even analysis because it helps to determine that level of output which will help the firm to cover its entire cost and thus to make profit. Breakeven point is the point where the firm starts making profit. Breakeven analysis is used in the business for following purposes.

Limitations

Q12) Discuss with the help of diagram how break-even point changes due to change in price and fixed cost. (8 marks)

A12)

Break-even analysis studies the relationship between total cost, total revenue, total profits and losses over a range of output. Break-even point is a point where the total revenue of the firm is equal to total cost. Therefore, at break-even point there is no profit, no loss.

Break-even analysis technique is used in the business to determine the level of production or sales volume which is necessary for the business to cover its cost of doing a business. In financial analysis the concept of break-even point is most commonly used

Changes in price

Any change in price will have an effect on total revenue and therefore also on break-even point.

If we consider the same example 1 and consider an increase in price to Rs.17, and keep fixed cost and average variable cost constant, break-even quantity is

QB = FC/ P-AVC

= 4000/17-7 = 4000/10 = 400 units

If we consider fall in price to Rs. 12, keeping fixed cost and average variable cost constant, break-even quantity is

QB = FC/P-AVC

= 4000/12-7 = 4000/5 = 800 units

This shows that with an increase in price, break-even quantity falls and with a fall in price, break-even quantity increases.

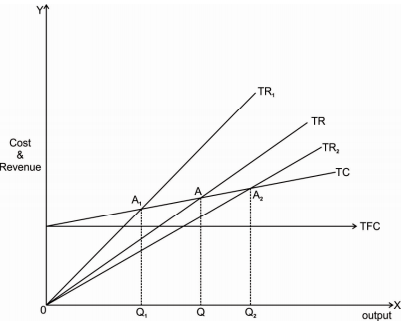
Effect of changes in price on break-even point and breakeven quantity can be explained with the help of following diagram.

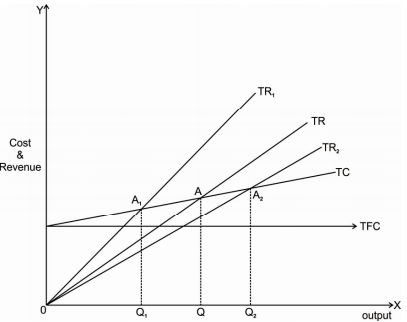
In the above diagram X axis measures output and Y axis measures cost and revenue. With an initial TR and TC curves A is the break-even point, where TR and TC curves intersects. If price increases, TR curve shifts upward from TR to TR1. This will bring down the break-even point from A to A1. Similarly, with a fall in price, TR curve shifts downward to TR2 and thus break-even point also shifts to A2.

Changes in fixed cost

For the same mathematical example 1 if we change the fixed cost and keep price and average variable cost constant, we have changes in breakeven quantity.

Suppose fixed cost increases to Rs. 5000, break-even quantity is

QB = FC/P-AVC = 5000/15-7 = 5000/8 = 625 units.

If fixed cost falls to Rs. 3600, break-even quantity is

QB = FC/P-AVC = 3600/15-7 = 3600/8 = 450 units

This shows that with an increase in fixed cost, break-even quantity increases and with a fall in fixed cost, break-even quantity falls.

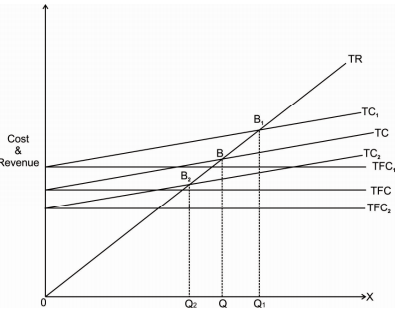
Changes in break-even point due to changes in fixed cost can be explained with the help of following diagram

On the X axis we measure output and on the Y axis we measure cost and revenue. With an initial TR and TC curves initial break-even point is B initial break even quantity is OQ if fixed cost increases, TFC curve shifts upward to TFC1. As total cost is the addition of TFC and TVC, TC curve will also shift upward to TC1. This shifts the break-even point at higher level to B1. Break even quantity has also increased from OQ to OQ1.

On the other hand, if TFC falls, TFC curve will shift downward to TFC2. This will shift the TC curve down to TC2. Therefore, new break-even point is B2 & new break even quantity falls from OQ to OQ2.

Q13) Explain changes in break-even point due to change in total variable cost? (5 marks)

A13)

Break-even analysis studies the relationship between total cost, total revenue, total profits and losses over a range of output. Break-even point is a point where the total revenue of the firm is equal to total cost. Therefore, at break-even point there is no profit, no loss.

Break-even analysis technique is used in the business to determine the level of production or sales volume which is necessary for the business to cover its cost of doing a business. In financial analysis the concept of break-even point is most commonly used

Changes in variable cost per unit

Using the same mathematical problem if we keep price and fixed cost constant and change the variable cost per unit, we have a change in break-even quantity.

Suppose the average variable cost per unit increases to Rs. 10, break-even quantity is

QB = FC/P-AVC

= 4000/15-10 = 4000/5 = 800 units.

If variable cost per unit falls to Rs. 5, break-even quantity is

QB = FC/P-AVC

= 4000/15-5 = 4000/10 = 400 units.

This shows that with an increase in per unit variable cost, break-even quantity increases and with a fall in average variable cost, break-even quantity falls.

This can be discussed with the help of following diagram

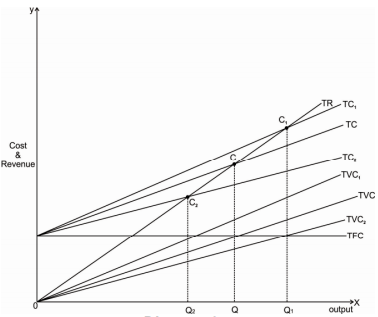
In the above diagram X axis measures output and Y axis measures cost and revenue. Initial break-even point is C where TR and TC curves intersect. Initial break even quantity is OQ. With an increase in TVC, TVC curve shifts to TVC1. This also shifts TC curve to TC1. TVC1 and TC are parallel to each other. Thus, the new break-even point shifts upward to C1 & break even quantity increases from OQ to OQ1.

With a fall in TVC, TVC curve shifts to TVC2, shifting down TC curve to TC2. Thus, the new break-even point also shifts down to C2. Again, TVC2 and TC2 are parallel to each other. New break even quantity falls from OQ to OQ2.

Q14) Explain changes in breakeven point due to price, fixed cost and variable cost. (8 marks)

A14)

Break-even analysis studies the relationship between total cost, total revenue, total profits and losses over a range of output. Break-even point is a point where the total revenue of the firm is equal to total cost. Therefore, at break-even point there is no profit, no loss.

Break-even analysis technique is used in the business to determine the level of production or sales volume which is necessary for the business to cover its cost of doing a business. In financial analysis the concept of break-even point is most commonly used.

Break-even point or break-even quantity changes due to change in following factors

Changes in break-even quantity and break-even point due to above factors can be discussed with the help of following example-

Changes in price

Any change in price will have an effect on total revenue and therefore also on break-even point.

If we consider the same example 1 and consider an increase in price to Rs.17, and keep fixed cost and average variable cost constant, break-even quantity is

QB = FC/ P-AVC

= 4000/17-7 = 4000/10 = 400 units

If we consider fall in price to Rs. 12, keeping fixed cost and average variable cost constant, break-even quantity is

QB = FC/P-AVC

= 4000/12-7 = 4000/5 = 800 units

This shows that with an increase in price, break-even quantity falls and with a fall in price, break-even quantity increases.

Effect of changes in price on break-even point and breakeven quantity can be explained with the help of following diagram.

In the above diagram X axis measures output and Y axis measures cost and revenue. With an initial TR and TC curves A is the break-even point, where TR and TC curves intersects. If price increases, TR curve shifts upward from TR to TR1. This will bring down the break-even point from A to A1. Similarly, with a fall in price, TR curve shifts downward to TR2 and thus break-even point also shifts to A2.

Changes in fixed cost

For the same mathematical example 1 if we change the fixed cost and keep price and average variable cost constant, we have changes in breakeven quantity.

Suppose fixed cost increases to Rs. 5000, break-even quantity is

QB = FC/P-AVC = 5000/15-7 = 5000/8 = 625 units.

If fixed cost falls to Rs. 3600, break-even quantity is

QB = FC/P-AVC = 3600/15-7 = 3600/8 = 450 units

This shows that with an increase in fixed cost, break-even quantity increases and with a fall in fixed cost, break-even quantity falls.

Changes in break-even point due to changes in fixed cost can be explained with the help of following diagram

On the X axis we measure output and on the Y axis we measure cost and revenue. With an initial TR and TC curves initial break-even point is B initial break even quantity is OQ if fixed cost increases, TFC curve shifts upward to TFC1. As total cost is the addition of TFC and TVC, TC curve will also shift upward to TC1. This shifts the break-even point at higher level to B1. Break even quantity has also increased from OQ to OQ1.

On the other hand, if TFC falls, TFC curve will shift downward to TFC2. This will shift the TC curve down to TC2. Therefore, new break-even point is B2 & new break even quantity falls from OQ to OQ2.

Changes in variable cost per unit

Using the same mathematical problem if we keep price and fixed cost constant and change the variable cost per unit, we have a change in break-even quantity.

Suppose the average variable cost per unit increases to Rs. 10, break-even quantity is

QB = FC/P-AVC

= 4000/15-10 = 4000/5 = 800 units.

If variable cost per unit falls to Rs. 5, break-even quantity is

QB = FC/P-AVC

= 4000/15-5 = 4000/10 = 400 units.

This shows that with an increase in per unit variable cost, break-even quantity increases and with a fall in average variable cost, break-even quantity falls.

This can be discussed with the help of following diagram

In the above diagram X axis measures output and Y axis measures cost and revenue. Initial break-even point is C where TR and TC curves intersect. Initial break even quantity is OQ. With an increase in TVC, TVC curve shifts to TVC1. This also shifts TC curve to TC1. TVC1 and TC are parallel to each other. Thus, the new break-even point shifts upward to C1 & break even quantity increases from OQ to OQ1.

With a fall in TVC, TVC curve shifts to TVC2, shifting down TC curve to TC2. Thus, the new break-even point also shifts down to C2. Again, TVC2 and TC2 are parallel to each other. New break even quantity falls from OQ to OQ2.

Q15) Suppose fixed cost for the firm is Rs. 4000, price per unit of output is Rs. 15 and the Average Variable Cost is Rs. 7, its breakeven quantity is-

A15)

BQ = FC/ P-AVC

4000/15-7

4000/8

Q= 500 units

Break-even sales volume can be calculated by multiplying break-even quantity by the price per unit of output.

BS = BQ*P

Where BS= Break-even sales volume

BQ= Break even quantity P= Price per unit

BS= 500*15

= Rs.7500