Unit-2
Permutation, Combination and Linear Programming Problems
Part-A
Q1) Explain the concept of permutation and combination and factorial. (8)
A1)
Suppose a man has a mobile phone and he sets a password of three digits from 0 to 9. Suppose the man forgets his 3 digits password. Then is there any technique which helps him to open the lock? The answer is yes. This answer is provided by the techniques of counting. In case of above situation, techniques of counting tell us how many different locking options ( the three digits codes) are possible with 3 numbers each containing 10 digits from 0 to 9. Out of these options, there is only one correct option. If the man starts to try them definitely at some stage, phone lock will get opened (because total number of options is finite in number). In our day to day life, there are many situations, where we need to count the number of ways a particular event can take place.
In these types of situations we use the concept of permutation, combination etc.
“The continued product of first n natural numbers, i.e., 1, 2, 3, …. (n – 1) n, is generally denoted by the symbol 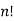 we read it as ‘factorial n”.
we read it as ‘factorial n”.
Expressed as-
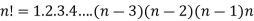
The product of first n natural numbers is denoted by n! and read as ‘n factorial’.
n! = n. (n –1) .…3.2.1
If n = 0, then we define 0! = 1
Q2) What do you understand by fundamental principal of counting. (7)
A2)
There are two fundamental principles of counting. These two principles solve the problems of counting. So it becomes necessary for us first to define what is the counting problem? According to Grinstead and Snell (2006) it is defined as if you “Consider an experiment that takes place in several stages and is such that the number of outcomes m at the nth stage is independent of the outcomes of the previous stages. The number m may be different for different stages. We want to count the number of ways that the entire experiment can be carried out.”
Fundamental principal of counting:
- The Sum Rule- Let us consider two tasks which need to be completed. If the first task can be completed in M different ways and the second in N different ways, and if these cannot be performed simultaneously, then there are M + N ways of doing either task. This is the sum rule of counting.
Example: Suppose one woman or one man has to be selected for a game from a society comprising 17 men and 29 women. In how many different ways can this selection be made?
Sol.
The first task of selecting a woman can be done in 29 ways. The second task of selecting a man can be done in 17 ways. It follows from the sum rule, that there are 17+29 = 46 ways of making this selection.
2. The Product Rule- Let us suppose that a task comprises of two procedures. If the first procedure can be completed in M different ways and the second procedure can be done in N different ways after the first procedure is done, then the total number of ways of completing the task is M × N
Example: suppose a teacher wants to select one boy and one girl student out of a class having 15 boys and 10 girls students, then teacher can make such selection in 15× 10 = 150 distinct ways.
Q3) How do we find the Permutation of things when they are not all different and n different things in a circle? (5)
A2)
To find the number of permutation of n things taken all together, the things are not all different.
Suppose that n things be represented by n letters and p of them be equal to a, q of them be equal to b and r of them be equal to c and the rest be all different. Let X be the required number of permutations.
X = n! /p ! q ! r !
N different things in a circle
When things are arranged in a row, we find two ends in each arrangement, while when the things are arranged in circle, there is no such end.
Thus the number of ways in which n different things can be arranged in a circle taking all together is (n – 1) !, since any one of the things placed first is fixed and remaining (n – 1) things can now be arranged in (n –1) ! ways.
Q4) Explain permutations. (8)
A4)
A permutation is an arrangement of objects in a definite order. Since we have already studied combinations, we can also interpret Permutations as ‘ordered combinations.
Permutation is related to the arrangement of things. Things arranged in a line come under the heading of linear permutation, while arrangement of things in a circle comes under the heading of circular permutation.
Linear Permutation
Possible arrangements in a line of a number of things taken some or all at a time are called the permutation.
Circular Permutation
If anticlock wise and clock wise order of arrangements makes different permutations then number of circular permutations of n distinct things = (n – 1)! And if anti-clock wise and clock wise order of arrangements does not give distinct permutations then total number of permutations of n distinct things = (n – 1)!/2
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 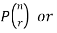
Note-
- The number of permutations of n different things taken r at a time in which p particular things never occur is-
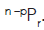
2. The number of permutations of n different things taken r at a time in which p particular things are always present is-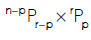
Q5) Write a short note on sampling with or without replacement. (7)
A5)
Suppose we chose the samples with repetition, from example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = 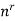
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
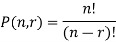
Theorem- The total number of permutations of n things taken r at a time any thing can repeat any number of times is given by n’.
Proof:
In order to find out total number of permutations, we have to fill up r positions, where
First position can be filled up in n ways,
Second position can also be filled up in n ways,]
Third position can be filled up in n way,
And so on
r’th position can be filled up in n ways.
So that, required number of permutations = n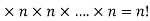
Q6) Explain combinations.(7)
A6)
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
“The different groups or collection or selections that can be made of a given set of things by taking some or all of them at a time, without any regard to the order of their arrangements are called their combinations.”
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
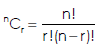
Total number of combinations:
Total number of combination of n different things taken 1, 2, 3 …. n at a time.
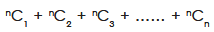
Note-
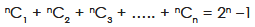
Note-
1. Property-1
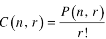
2. Property-2
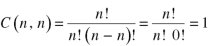
3. Property-3
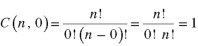
Part-B
Q7) There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row? (5)
A1)
Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =
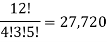
Q8) In how many ways 6 children can be arranged in a line, such that (7)
(i) Two particular children of them are always together
(ii) Two particular children of them are never together
A2)
(i) The given condition states that, 2 students needs to be together, hence we can consider them 1.
Thus, the remaining 7 gives the arrangement in 5! ways, i.e. 120.
Also, the two children in a line can be arranged in 2! Ways.
Hence, the total number of arrangements will be,
5! × 2! = 120 × 2 = 240 ways
(ii) The total number of arrangements of 6 children will be 6!, i.e. 720 ways.
Out of the total arrangement, we know that, two particular children when together can be arranged in 240 ways.
Therefore, total arrangement of children in which two particular children are never together will be 720 – 240 ways, i.e. 480 ways.
Q9) Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed? (8)
A3)
Number of ways of selecting 3 consonants from 7
= 7C3
Number of ways of selecting 2 vowels from 4
= 4C2
Number of ways of selecting 3 consonants from 7 and 2 vowels from 4
= 7C3 × 4C2
= 210
It means we can have 210 groups where each group contains total 5 letters (3 consonants and 2 vowels).
Number of ways of arranging 5 letters among themselves
= 5! = 5 × 4 × 3 × 2 × 1 = 120 = 5! = 5 × 4 × 3 × 2 × 1 = 120
Hence, required number of ways
= 210 × 120 = 25200
Q10) In how many ways 15 things be divided into three groups of 4, 5, 6 things respectively. (5)
A4)
The first group can be selected as-
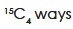
The second group can be selected as-
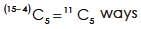
The third group can be selected as-
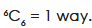
Hence the total number of ways-
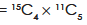
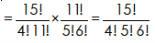
Q11) In how many ways can be letters of the word TABLE be arranged so that the vowels are always (i) together (ii) separated ? (5)
A5)
(i)
In the word there are 2 vowels, 3 consonants all different. Taking the 2 vowels (A, E) as one letter we are to arrange 4 letters (i.e. 3 consonants + 1) which can be done in 4 ! ways. Again 2 vowels can be arranged among themselves in 2 ! ways.
Hence, required number of ways = 4! × 2! = 48.
(ii) Without any restriction (i.e. whether the vowels, consonants are together or not) all the different 5
Letters can be arranged in 5! ways. Arrangement of vowels together is 48 (shown above)
Hence, Required number of ways = 5! – 48 = 120 – 48 = 72.
Q12) In how many ways can be letters of the word SUNDAY be arranged? How many of them do not begin with S? How many of them do not begin with S, but end with Y? (5)
A6)
There are 6 letters in the word SUNDAY, which can be arranged in 6! = 720 ways.
Now placing S in first position fixed, the other 5 letters can be arrange in (5)! = 120 ways.
The arrangements of letters that do not begin with S = (6) ! – (5) ! = 720 – 120 = 600 ways.
Lastly, placing Y in the last position, we can arrange in (5) ! = 120 ways and keeping Y in the last position and
S in the first position, we can arrange in (4) ! = 24 ways.
Hence, the required no. Of arrangements = (5) ! – 4 ! = 120 – 24 = 96 ways.
Q13) Given n points in space, no three of which are collinear and no four coplanar, for what value of n will the number of straight lines be equal to the number of planes obtained by connecting these points? (5)
A7)
Since no three points, are collinear, the number of lines = number of ways in which 2 points can be selected out of n points
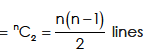
Again since three non-collinear points define a space and no four of the points are coplaner; the number of planes = number of ways in which 3 points can be selected out of n points.
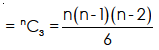
Now, we have
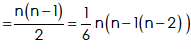
Or
6 = 2 (n – 2) Hence, n = 5
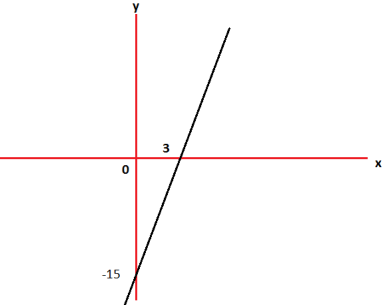
Q14) Draw the graph for the linear equation y - 5x + 15=0. (7)
A8)
The given equation can be written as-
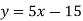
x-intercept-
When y = 0, we get-
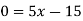
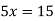
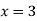
y-intercept-
When x = 0, we get-
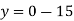
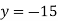
Q15) In a sports broadcasting company, the manager must pick the top three goals of the month, from a list of ten goals. In how many ways can the top three goals be decided? (5)
A9)
Since the manager must decide the top three goals of the month; the order of the goals is very important! It decides the first-place winner, the runner-up, and the second runner-up. Thus, we can see that the problem is of permutation formula.
Picking up three goals from a list of ten:
Possible Permutations = 10P3 = 10!(10−3)! = 10 × 9 × 8 = 720
Therefore, there are 720 ways of picking the top three goals!
Q16) A magic show has ten people in the audience. For the next act, the magician needs two people from the audience. In how many ways can he invite the two people from his audience? (8)
A10)
What we mean by the number of ways is actually how many different pairs of people can he invite up to the stage. For e.g. Suppose that we have five friends Tim, John, Robin, Alice and Sarah in the audience along with five other people.
Now, the magic trick can be conducted equally well by inviting say, John and Alice to the stage; as well as by inviting Tim and Robin to the stage. Thus, we need to find out the number of all such pairs which can lead to a success of the magic trick.
We must choose 2 people out of the total 10 people. Thus, according to the formula, we have n = 10 and r = 2. Then,
10C2 = 10!2!(10−2)!
It can be solved by expanding the factorial in the numerator:
= 10.9.8!2!.8! → 10.91.2
= 45
Hence there are 45 ways in which the magician can select two people from his audience of ten. This is what you mean by the number of combinations of two people from a total of ten people.
Q17) A manufacturer produces two types of for children, mouth – organs and drums, each of which must be processed through two machines A and B. The Maximum availability of machines A and B per day are 12 and 18 hours respectively. The manufacturing a mouth – organ requires 4 hours in machine A and 3 hours in profit per mouth – organ is Rs 20 and per drum is Rs 50, machine A and 6 hours of machine B. If the profit per mouth-organ is RS 20 and per drum is Rs 50, formulate the problem to maximize the profit. (8)
A11)
Let us suppose that, the manufacturer produces X mouth- organs and y drums per day. Then tabulating the given data as follow, we observe that, if x mouth –organs and y drums are manufactured per day, he will require 4x + 2y hours of machine A and 3x + 6y hours of machine B.
Machine | Mouthorgan (x) | Drum (y) | Maximum available |
A | 4 | 2 | 12 |
B | 3 | 6 | 18 |
Since the availability of the machine A and B are not more than 12 and 18 hours respectively, we must have 4x + 2y 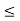 12 and 3x + 6y
12 and 3x + 6y 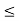 18.
18.
Note that, he may not able to complete a mouth – organ or a drum in a daytherefore, x or y need not be integers, but x and y can never be negative, since nobody can manufacture a negative number of objects. Hence, the condition
X30 , y3 0 will be implemented
Thus, the problem written mathematically will be
4x +2y 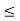 12
12
3x + 6y 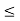 18 and
18 and
x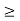 0, y
0, y 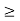 0
0
These inequalities are the constraints on the problem.
Now to find the objective function.
Since the profit per mouth – organ and drum are RS 20 RS 50 respectively, the objective function would be
Profit z = 20x + 50y, which is to be maximized
Under the constraints given above.
Q18) Solve graphically, the following lpp problem (8)
Maximise z=9x +13y,subject to
2x + 3y 18
18
2x +y  10,
10,
x  0
0
y  0
0
A12)
Step 1>>Draw the lines 2x +3y =18 and 2x + y=10
And obtain the feasible region given by OAPBO
Step 2>>The optimum solution is at one of the corners O,A,P,B of the feasible region
Therefore,we need to find the coordinates of these corners
O,A and B are already known to be (0,0),(5,0) and (0,6) respectively.
To find P, observe that, it is the point of intersection of the lines 2x +3y =18 and 2x + y=10
Therefore, solvingthis equation simultaneously, we will get the coordinates of P
2x +3y =18
2x + y=10
Subtracting, 2y = 8
Y = 4
Substituting y=4 in 2x + y=10
We get 2x + 4=10 i.e.2x=6
x=3
Hence the point p is (3,4).
Step 3>> check the values of z=9x +13y , at each of these corners .
At O(0,0), z= 9(0) + 13(0)=0
At A(5,0), z= 9(5) + 13(0)= 45
At P(3,4), z= 9(3) + 13(4)= 79
At B(0,6), z= 9(0) + 13(6)= 78
Therefore, the maximum value of z occurs at P(3,4)
Therefore, the optimum solution of the L.P. Problem is x=3, y=4 and the optimum value of z is 79.
Q19) Solve the following LPP graphically- (8)
Maximize-
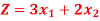
Subject to the constraints-
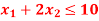
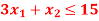
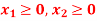
A13)
Change the given constraints into equations-
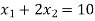
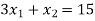
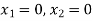
The line 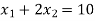 meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
Hence origin (0,0) satisfies the inequality 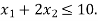 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of 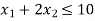 .
.
And
The line 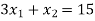 meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
Hence origin (0,0) satisfies the inequality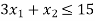 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of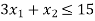 .
.
Now all the points in first quadrant satisfies 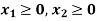 .
.
So that first quadrant is the region represented by 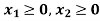
Hence the region OCEBO satisfies all the inequalities.
And each point on the region is the feasible solution of the problem.
Feasible solution-
Here in this problem the feasible solution is (5,0), (4,3) and (0,5).
Now we can obtain the optimal solution of the problem.
As we know that any point in the feasible region that gives the optimal value is called an optimal solution.
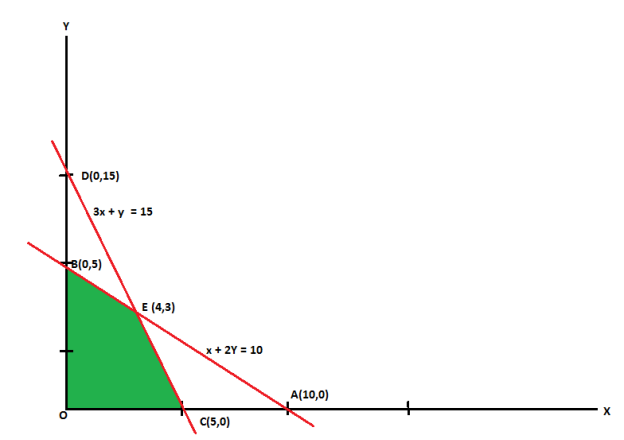
The value of the objective function 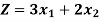 at corner points of the feasible region is given below-
at corner points of the feasible region is given below-
Vertex [ feasible region ] | Value of 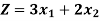 |
O(0,0) | 0 |
C(5,0) | 15 |
E(4,3) | 18 [Maximum] |
B(0,5) | 10 |
Here we see that the maximum value of Z is 18.