OR
Unit IVJob Sequencing and Theory of Games Q1) Define Job Sequencing Problem with an example.A1) If the work is done before the deadline, given an assortment of jobs where every job has a deadline and associated benefit. Each work often needs a single unit of time, so the minimum possible deadline for every job is 1. How to optimize overall benefit because it is possible to plan just one job at a time.Example 1: Input: Four jobs with the following information:Deadlines and earnings
Output: The limit is followed byProfit series of employment positionsC, a, a, a Example 2:Input: Five jobs with the following information:Deadlines and earnings
Output: The limit is followed byProfit series of employment positionsC, a, f, and e, Q2) Explain Processing Maximum 9 Jobs through Two Machines only.A2)Example There are nine jobs, each of which must go through two P and Q machines in the order PQ, below are the processing times (in hours):
Task: Find the series to minimize the cumulative time T has elapsed. Calculate the overall idle time during this period for the machines as well.Solution: On two machines, the minimum cycle time is 2 corresponding to task A on machine P. This means that task A would first precede it. We are left with 8 tasks on two machines after assigning task A.
In this reduced problem, the minimum processing time is 3, corresponding to jobs E and G (both on machine Q). Now that the corresponding processing time of task E on machine P is lower than the corresponding processing time of task G on machine Q, task E will be processed in the last one and task G will be processed in the next one. The scenario will be dealt with as
The problem now decreases to 6 tasks with processing time on two computers, as follows:
Here since the minimum processing time is 4 which occurs for tasks C and I on machine P and task D on machine Q. Therefore, the task C which has less processing time on P will be processed first and then task I and task D will be placed at the last i.e., 7th sequence cell.The sequence will appear as follows:
The problem now decreases to the following 3 duties on two machines.
The minimum processing time in this reduced table is 5, which occurs both on machine P for tasks B and H. Now that the corresponding time is the same for tasks B and H on machine Q, i.e., 8. In the 4th and 5th sequence cells, tasks B or H may be arbitrarily placed. It is then possible to place the remaining task F in the 6th sequence cell. Therefore, the optimal sequences are portrayed as
or
Furthermore, the minimum elapsed time corresponding to the optimal sequence A → I → C → B → H → F → D → E → G can also be calculated.
Therefore, the total time elapsed for this proposed sequence from job A to job G completion is 61 hours. Machine P remains idle for 11 hours during this time (from 50 hours to 61 hours) and machine Q remains idle for only 2 hours (from 0 hour to 2 hour). Q3) With help of numerical based problem explain Processing Maximum 6 Jobs through Three Machines only.A3) Via three stages of processing, viz., cutting, stitching & pressing, Shahi Export House has to process five products. In the following table, processing times are given:
Determine the order in which these objects should be handled so that the overall processing time is reduced.The processing times are given below for the new issue.
Thus, in each of the two forms, the ideal sequence can be created.
Total elapsed time = 42Idle time for cutting process = 42 – 25 = 17 hours
Idle time for sewing process = 3 + (8 - 6) + (10 - 9) + (17 - 15) + (25 - 19) + (42 - 29) = 27 hours.
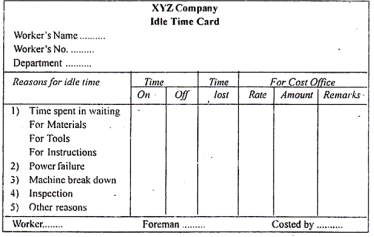
Idle time for pressing process = 6 + (11 - 11) + (18 - 18) + (24 - 24) + (34 - 34) = 6 hours. Q4) Define idle time with its types.A4) Attendance time must match work time. In general, it doesn't happen for many reasons. Examples-Time required to walk from the factory gate to the department, materials, tools, time lost to wait for instructions, loss due to machine failure, power outages, etc. This wasted time is called idle time. .. The idle time card is provided to check the idle time. The idle time card shows the reason for the idle time, so you can take action to prevent avoidable idle time.A sample idle time card is shown below
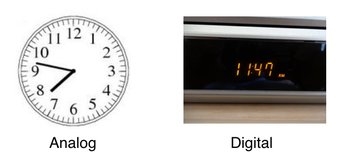
Idle time type:Idle time can be divided into two categories based on the cause or reason for its occurrence.(A) Normal idle time.(B) Abnormal idle time.(A) Normal idle time:This is unique to all types of employment and cannot be avoided. The cost of this time is borne by each job or product or department.An example of normal idle time is shown below.(1) The time it takes for a worker to walk from the gate to the department.(2) Time is required to receive tools, change clothes and receive work instructions.(3) The time it takes to change from one job to another.(4) Personal needs and time required for tea.(5) Wait time for the machine to be ready for production work (called setup time).Normal idle time processing:There are two ways to charge your production environment during normal idle time:(1) Normal idle time costs will be factory costs and will be collected as indirect costs.(2) Normal idle time costs are charged directly to production as direct wages.(B) Abnormal idle time:Abnormal idle time is the avoidable idle time caused by preventable conditions.The reasons why the idle time is abnormal are as follows.(1) Time lost due to machine failure,(2) Time lost due to a power outage.(3) Loss of time due to lack of materials.(4) Wasted time because there is no instruction. And(5) Time lost due to strikes and lockouts.Handling of abnormal idle time:The basic principle of costing is to eliminate the impact of all anomalous losses and profits on a job or process or operation by transferring all anomalous costs and profits to the income statement. They should not form part of the production cost. Wages paid for abnormal idle time are charged to the costing profit and loss account.Idle time control: It is necessary to analyse the reasons for idle time and take measures to prepare for all contingencies, such as preventive maintenance of machines, proper arrangements to provide sufficient materials, preparation of work instructions in advance, and avoidance of strikes there is. Even normal idle time can be controlled by efficient management planning and supervision. Q5) What is elapsed time?A5) Elapsed time is the time elapsed between the two specified times. At the end of this lesson, you can calculate how long it will take to do something, or how long it will take for something to start. Let's get started!Clock typeYou know that clocks are used to convey time. There are two main types of watches we see every day. Learn about them now.An analog clock is a circle with the numbers 1-12 on the edge and at least two moving hands. A digital clock is a clock that displays the time in 3 or 4 digits as a visual example, start by using an analog clock to calculate the elapsed time.
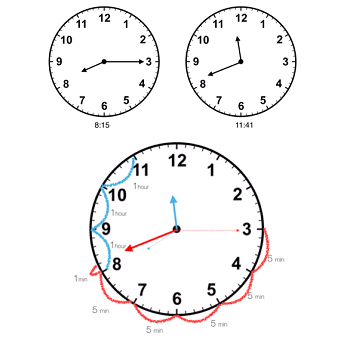
Elapsed time in analogAnalog and digital clocksRemember that on analog clocks, the short hands point to the hour and the long hands point to the minute. In the pictures showing both types of clocks, the analog clock shows 7:47. As the long needle moves for 24 hours, it touches each short line. These are equivalent to 1 minute. The numbers represent the passage of 5 minutes. After 60 minutes have passed since the long hand made one lap, the short hand moved to the next number, indicating that one hour had passed.ExampleLet's try it with an example. Jeremiah arrives at school at 8:15 am. He is doing a special project in science and is very excited. Science begins at 11:41 am. How long does Jeremiah have before the science class begins?
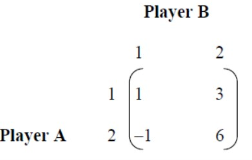
Q6) Write note on Game theory.A6) Game theory is a theoretical framework for imagining social situations between competing players. In some respects, game theory is the best decision of an independent competing actor in the science of strategy, or at least in a strategic setting. Let's look at some examples.The major pioneers of game theory were the 1940s mathematician John von Neumann and the economist Oskar Morgenstern. Mathematician John Nash is considered by many to provide the first significant extension of the work of von Neumann and Morgenstern! Q7) How will you explain the Basics of game theory? Do mention the Nash equilibrium.A7) The focus of theory of games may be a game that acts as a model for an interactive situation between rational players. The key to game theory is that the rewards of one player depend on the strategy implemented by the other player. The game identifies the player's identity, preferences, available strategies, and how these strategies affect results. Depending on the model, various other requirements and assumptions may be required. According to game theory, the actions and choices of all participants influence their outcomes!Let's start with Nash equilibriumNash equilibrium is the result reached, which means that once achieved, the payoff cannot be increased by unilaterally changing decisions. You can also think of it as "no regrets" in the sense that once you make a decision, you will not regret a decision that takes into account the consequences.In most cases, the Nash equilibrium is achieved over time. However, once the Nash equilibrium is reached, it does not deviate. After learning how to find the Nash equilibrium, let's see how unilateral movements affect the situation. Does it make sense? The Nash equilibrium is described as "no regrets" because it should not be. It is generally believed that there are multiple equilibrium in a game.This mainly happens in games that have more complex elements than the two choices of two players. In a simultaneous game that repeats over time, one of this multiple equilibrium is reached after trial and error. This scenario of various overtime choices before reaching equilibrium is most often performed in the business world when two companies are deciding on prices for compatible products such as airfares and soft drinks. The impact of game theory on economics and businessGame theory has revolutionized economics by addressing the critical problems of previous mathematical economic models. Neoclassical economics, for example, struggled to understand the expectations of entrepreneurs and was unable to cope with imperfect competition. Game theory turned its attention to the market process itself from steady-state equilibrium.In business, game theory is undoubtedly useful for modelling competing behaviour between economic agents. Enterprises often have several strategic options that affect their ability to achieve economic benefits. For example, companies may face dilemmas such as discontinuing existing products, starting new product development, lowering prices compared to competitors, or adopting new marketing strategies. Economists tend to use game theory to understand the behaviour of oligopolistic businesses. This helps predict the possible consequences of a company engaging in certain actions such as price fixing or collusion. Q8) What do you mean by Repeated oligopoly game?A8) The prisoner's dilemma was played once by two players. Players were given a payoff matrix. Each can make one choice and the game ended after the first selection round.In the real world of oligopoly, there are as many players as companies in the core industry. They play round by round: the company raises its price. When another company introduces a new product and the first company cuts prices, the third company introduces a new marketing strategy. Oligopoly games are a bit like baseball games, with no limit on the number of innings. One company will play one round later and another will be on top on another day. Example: In games in the computer industry, the rules have changed with the introduction of personal computers. Very easy to win in mainframe games, IBM is struggling to keep up with a world where rivals continue to lower prices and improve quality.The oligopoly game can have more than two players, so the game is much more complicated, but the basic structure remains the same. The fact that the game itself repeats brings new strategic considerations. Players need to consider how their choices will affect their rivals in the future, not how their choices will affect their rivals.Now keep the game simple and think about duopoly games. The two companies have colluded implicitly or openly to create an exclusive solution. As long as each player just supports the agreement, the two companies will get exactly the maximum financial benefit possible for the company. Q9) What is Decision process?A9) Game theory is about making decisions in an interactive world, so the best decisions of all decision makers depend on what others make. As a result, everyone in this interactive world needs to anticipate the decisions of others in order to promote their own interests.This was a collaboration between Austrian economist Oskar Morgenstern and Hungarian genius, polymath and multilingually acclaimed John von Neumann.Von Neumann was an undisputed genius, but he quickly realized that he was a mediocre poker player and couldn't beat poker games in probability theory. His great appreciation for the rough information, secondary guesses, and unpredictability of poker games laid the very foundation for game theory. Poker players can hide information by strategically releasing it through movements and encouraging mistakes from rivals.In other words, he formalized how poker players "bluff" their rivals by tricking them into hiding information and playing with a set of strategies that are ultimately supposed to win the game.John Nash's legacy in game theory is a unique and achievable Nash equilibrium, and therefore game theory has become completely clinical and completely excluded from the real world. The only exceptions among skilled economists today are two other Nobel laureates, Thomas C. Schelling and Roger Myerson. Q10) Define the Terminology of Game Theory: Players, Strategies, Play, Payoff, Payoff matrix, Maximin, Maximax, Saddle Point.A10) PlayersA strategic decision-maker inside the game's context.StrategiesGiven the collection of situations that might occur within the game, a full course of action a player would take. PlayAny set of criteria that have an effect based on the decisions of two or more decision-makers (players)PayoffThe pay-out that a player gets from a single result. The payoff can be from dollars to utilities in any quantifiable manner,Payoff matrixIn game theory, a payoff matrix is an important tool because it summarizes theIt helps us determine whether there is a dominant strategy or an Optimal Mixed strategy or a Nash equilibrium. Pay off matrices are commonly used in Economics while representing a Duopoly or Oligopoly model game.MaximinThe maximin individual looks at the worst that could happen under each action and then selects the largest payoff action. They assume that it will be the worst that can happen, and then they take the best-worst-case scenario action. The minimum maximum or "best of the worst" maximum. This is the person who puts his or her funds into a bank account so the stock market will lose money.MaximaxThe Maximax looks at the best that could occur under each action and then selects the greatest value action. They assume they're going to get as much as possible and then they take the best-case scenario action. The maximum Maximax or "best of the best" maximum. This is the lotto player; large payoffs are seen and the probabilities are ignored.Saddle pointA point where a function of two variables has partial derivatives equal to zero, so where there is neither a maximum nor a minimum value for the function. Q11) Determine which of the following two-person zero-sum games are strictly determinable and fair. Give optimum strategies for each player in the case of strictly determinable games:
(b) 
A11) The payoff matrix for player A is
The payoffs marked with [*] in each row reflect the minimum payoff and the payoffs marked with [+] in each column of the payoff matrix represent the full payoff. 
(maximinim) is the largest portion of the minimum lines.Value) and the smallest Column Maximum part represents 
(minimax value).Thus obviously, we have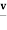 
=0 and 
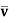2. Since 
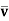, the game is not strictly determinable. Q12) Consider the example of solving a game whose pay-off matrix is given as follows in the following table:Issue of the Game
A12) The game is worked out using the minimax method. In each row, find the smallest value and select the largest value from these values. Next, in each column, find the largest value and pick the smallest of these numbers. The following table shows the procedure. Minimax Procedure
If Maximum value in row is equal to the minimum value in column, then saddle point exists.
Max Min = Min Max
1 = 1Therefore, there is a saddle point.
The strategies are,
Player A plays Strategy A1, (A A1).
Player B plays Strategy B1, (B B1).
Value of game = 1.
JobID | Deadline | Earning |
|
|
|
a | 4 | 20 |
b | 1 | 10 |
c | 1 | 40 |
d | 1 | 30 |
JobID | Deadline | Earning | |||
|
|
| |||
a | 2 | 100 | |||
b | 1 | 19 | |||
c | 2 | 27 | |||
d | 1 | 25 | |||
e | 3 | 15 | |||
Machine | Job(s) | ||||||||
A | B | C | D | E | F | G | H | I | |
P | 2 | 5 | 4 | 9 | 6 | 8 | 7 | 5 | 4 |
Q | 6 | 8 | 7 | 4 | 3 | 9 | 3 | 8 | 11 |
Machine | B | C | D | E | F | G | H | I |
P | 5 | 4 | 9 | 6 | 8 | 7 | 5 | 4 |
Q | 8 | 7 | 4 | 3 | 9 | 3 | 8 | 11 |
A |
|
|
|
|
|
| G | E |
Machine | B | C | D | F | H | I |
P | 5 | 4 | 9 | 8 | 5 | 4 |
Q | 8 | 7 | 4 | 9 | 8 | 11 |
A | C | I |
|
|
| D | E | G |
Machine | B | F | H |
P | 5 | 8 | 5 |
Q | 8 | 9 | 8 |
A | I | C | B | H | F | D | E | G |
A | 1 | C | H | B | F | D | E | G |
Job Sequence | Machine A | Machine B | ||
Time In | Time Out | Time In | Time Out | |
A | 0 | 2 | 2 | 8 |
I | 2 | 6 | 8 | 19 |
C | 6 | 10 | 19 | 26 |
B | 10 | 15 | 26 | 34 |
H | 15 | 20 | 34 | 42 |
F | 20 | 28 | 42 | 51 |
D | 28 | 37 | 51 | 55 |
E | 37 | 43 | 55 | 58 |
G | 43 | 50 | 58 | 61 |
Item | Cutting | Sewing | Pressing |
1 | 3 | 3 | 5 |
2 | 8 | 4 | 8 |
3 | 7 | 2 | 10 |
4 | 5 | 1 | 7 |
5 | 2 | 5 | 6 |
Item | Gi = Ai + Bi | Hi = Bi + Ci |
1 | 6 | 8 |
2 | 12 | 12 |
3 | 9 | 12 |
4 | 6 | 8 |
5 | 7 | 11 |
1 | 4 | 5 | 3 | 2 |
4 | 1 | 5 | 3 | 2 |
Item | Cutting | Sewing | Pressing | |||
| Time in | Time out | Time in | Time out | Time in | Time out |
1 | 0 | 3 | 3 | 6 | 6 | 11 |
4 | 3 | 8 | 8 | 9 | 11 | 18 |
5 | 8 | 10 | 10 | 15 | 18 | 24 |
3 | 10 | 17 | 17 | 19 | 24 | 34 |
2 | 17 | 25 | 25 | 29 | 34 | 42 |
Idle time for sewing process = 3 + (8 - 6) + (10 - 9) + (17 - 15) + (25 - 19) + (42 - 29) = 27 hours.
Idle time for pressing process = 6 + (11 - 11) + (18 - 18) + (24 - 24) + (34 - 34) = 6 hours. Q4) Define idle time with its types.A4) Attendance time must match work time. In general, it doesn't happen for many reasons. Examples-Time required to walk from the factory gate to the department, materials, tools, time lost to wait for instructions, loss due to machine failure, power outages, etc. This wasted time is called idle time. .. The idle time card is provided to check the idle time. The idle time card shows the reason for the idle time, so you can take action to prevent avoidable idle time.A sample idle time card is shown below
|
|
|
(a) 
(b) A11) The payoff matrix for player A is Player A | Player B | Row minima | |
B1 | B2 | ||
A1 | 5+ | 0* | 0 |
A2 | 0* | 2+ | 0 |
Column maxima | 5 | 2 |
|
(maximinim) is the largest portion of the minimum lines.Value) and the smallest Column Maximum part represents (minimax value).Thus obviously, we have 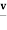=0 and 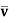2. Since 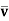, the game is not strictly determinable. Q12) Consider the example of solving a game whose pay-off matrix is given as follows in the following table:Issue of the Game
|
|
Max Min = Min Max
1 = 1Therefore, there is a saddle point.
The strategies are,
Player A plays Strategy A1, (A A1).
Player B plays Strategy B1, (B B1).
Value of game = 1.
0 matching results found