undefined | unit 3 network analysis

Back to Study material

UNIT 3NETWORK ANALYSIS Q1) What is the Critical Path Method? Describe its various concepts in brief.A1) Critical Path MethodThe critical path method (CPM), also known as critical path analysis (CPA), is a scheduling procedure that uses a network diagram to depict a project and the sequences of tasks required to complete it, which are known as paths.The essential technique for using CPM is to construct a model of the project that includes the following:

A list of all tasks required to complete the project

The dependencies between the tasks

The estimate of time (duration) that each activity will take to complete.

The concepts in CPM are as follows:ActivityEvery project consists of several job operations or tasks which are called activities. An activity is shown by an arrow and it begins and ends with an event. Activity consumes time and resources. An activity may be performed by an individual or a group of individuals.EventAn event represents a point in time signifying the completion of some activities and the beginning of new ones. This is usually represented by a circle in a network which is also called a node or connector.

Network diagram A project schedule network diagram visualizes the sequential and logical relationship between tasks in a project setting. This visualization relies on the clear expression of the chronology as it pertains to these tasks and events.Most often, a project network diagram is depicted as a chart with a series of boxes and arrows. This network diagram tool is used to map out the schedule and work sequence for the project, as well as track its progress through each stage — up to and including completion. Because it encompasses the large tasks that need to occur over the project’s duration, a network diagram is also useful in illustrating the scope of the project. Merge eventWhen more than one activity comes and joins an event such an event is known as a merge event.

Burst event When more than one activity leaves an event such an event is known as a burst event.

Concurrent activityActivities that can be accomplished concurrently are known as concurrent activities. It may be noted that an activity can be a predecessor or a successor to an event or it may be concurrent with one or more of other activities. Burst Activity: An activity that has more than one activity immediately following it (more than one dependency arrow flowing from it). Q2) Describe the Activity on node (AON) method. A2) The priority projection shows the connection of activities. Therefore, it's a crucial communication tool for stakeholders.

Precedence Diagramming Method (PDM)

The priority projection is formed from rectangles called nodes. These boxes show the activity of the project. The arrow connects the 2 boxes and shows the connection. Therefore, these diagrams are called activity (AON) diagrams on the node.AON dependency typeAON uses four dependencies.

Mandatory dependencies

Discretionary

External dependencies

Internal dependency

1. Mandatory dependenciesThis dependency is additionally referred to as hard logic. You cannot avoid it. The beginning of subsequent activity depends thereon.For example, you can’t install a ceiling until you’ve got built all the walls.2. DiscretionaryThis dependency also referred to as preferred logic or soft logic, is liable for optimizing resources.For example, you’ll create four walls in any order. However, if it’s beneficial to create them during a particular order, build them therein order.Here you’ll change the sequence of activities consistent with your favorite logic.3. External dependenciesThe project management team has no control over external dependencies.For example, government approval could also be required before subsequent activity can begin. 4. Internal dependencyThese dependencies are under the control of the project or organization.For example, you can’t get a resource until you’re released from another project.DependencyThe AON Method uses four relationships:

End to start (FS)

Finish to end (FF)

Start to Start (SS)

From start to finish (SF)

End to start (FS)

In this method, you can't start subsequent activity until the primary activity is complete. This is often the foremost common relationship in AON.

End and begin (FS) relationship

For example, to color a wall, you initially got to create the wall. During this case, the primary activity is building the wall, and therefore the second activity is painting. You can't start painting the wall until the wall is prepared.

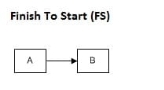
Finish To Start (FS) Relationship

Finish ending (FF)

Here, you can't complete subsequent activity until the primary activity is completed. Simply put, you would like to end both activities at an equivalent time.

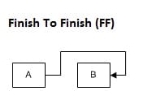
Finish To Finish (FF) Relationship

Relationship from end to finish (FF)

For example, for instance, you're coding a program for a client. The client will provide the functionality after completing the milestone. you can't complete the coding until you've got the complete requirements of the client. Here you would like to end both activities at an equivalent time.

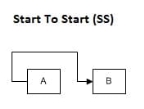
Start To Start (SS) Relationship

Start to Start (SS)

Here, subsequent activity can't be started until the primary activity is started. Both activities must start at an equivalent time.

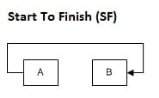
Start To Finish (SF) Relationship

Start-to-start (SS) relationship

Suppose you would like to use a coating to the wall, but you would like to wash the wall to use it.Therefore, one team cleans the wall, and therefore the second team coats the wall. You’ll start both activities at an equivalent time.

From start to finish (SF)

Here, you can't finish the subsequent activity until the primary activity has started.

Start-to-end (SF) relationship

For example, you're moving to a replacement house and you've got to demolish your old house. During this case, you'll not be ready to move to your new home until you're ready. Therefore, the second activity (building a replacement home) must be completed before the primary activity (moving to a replacement home) begins.Simply put, you're moving to your new home. You can't leave an old house until the new one is prepared.This relationship is rare, but you would like to know all the dependencies. Helps you draw a network diagram and schedule your project. Q3) Define Dummy activity and state its uses. A3) Dummy activities are some sort of simulated activity that has zero duration and is created solely to show the path of a particular relationship and action in the manner shown by the arrows. Dummy activities are useful for implementing specific logical relationships between two specific activities in arrow projection once you cannot specifically link or conceptualize them just by using arrows that move from one activity to another. It is a tool. In this case, creating a dummy activity that essentially acts as a placeholder format can provide something of great value. Dummy activities should not be assigned for any period in planning and/or scheduling or project activities and components. When they are shown in graphic format, dummy activities must be represented by a dashed user with an arrow at one end, and in some cases in a unique color.Uses of Dummy activities:

If two paths in your network have common events but are otherwise independent, you may get a logical error. This problem can be solved by separating the two (more or less) independent paths, introducing a dummy activity, and linking the completion of the data structure design to the start of the ordering activity. This effectively breaks the link between the data structure design and the order.

Dummy activities, where two activities share the same start and end nodes, make it easy to distinguish between activity endpoints.

If there is a time lag in parallel activities, you may see this as an activity ladder. In this case, the documentation can proceed in parallel with the prototype test as long as it starts for at least one day.

Q4) Draw a network for the simple project of the erection of steelworks for a shed. The various elements of a project are as under:

A4)

Q5) Define the following terms: Critical Path, Sub-critical Path, Critical and Non-critical Activities, Project Completion Time. A5) Critical pathThe critical path is the longest sequence of activities in a project plan which must be completed on time for the project to complete on the due date. Activity on the critical path cannot be started until its predecessor activity is complete; if it is delayed for a day, the entire project will be delayed for a day unless the activity following the delayed activity is completed a day earlier. Sub-critical pathThe sub-critical path means the second-longest path in the network. It is shorter than the critical path but longer than all other paths in the network. All activities on the sub-critical path are not critical. Some of the activities may be critical. Critical activitiesCritical activities are the project tasks that must start and finish on time to ensure that the project ends on schedule. A delay in any critical activity will delay the completion of the project unless the project plan can be adjusted so that successor tasks finish more quickly than planned. Non-critical activitiesActivities that can be pushed beyond their allotted deadline (up to the slack time) without affecting the project due date are called non-critical activities. Project completion timeWhen you have calculated the duration of the critical path, you can determine what the expected time of project completion is. Adding the time it takes to complete the tasks on the critical path to the starting date gives you the completion date according to the time estimation definition. You can maintain this date as long as you complete every critical activity within its projected duration. At the same time, you have to monitor the other activities of the project for delays. Q6) Describe the procedure for the Forward pass and Backward pass method.

A6) Forward pass method (For Earliest event time):

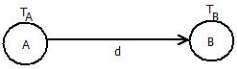
Based on the fixed occurrence time of the initial network event, the forward pass computation yields the earliest start and earliest finish times for each activity and indirectly the earliest expected occurrence time for each event.This consists of the following steps:

The computation begins from the start node and moves to the ‘end’ node. To accomplish this, the forward pass computations start with an assumed earliest occurrence time of zero for the initial project event.

i.e. E1 = ; i = 1

2. Calculate the earliest start time for each activity that begins at the event i. This is equal to the earliest occurrence time of event i (Tail event) i.e., ESij = Ei for all activity (i, j) starting from the event i.

3. Calculate the earliest finish time of each activity (I, j) which is the earliest start time of the activity plus the duration of the activity, i.e.

EFij = ESij + tij= Ei + tij 4. Calculate the earliest occurrence time for event j (J > i) which is the maximum of the earliest finish times of all activities ending into that event, i.e.Ej = Maximum (ESij + tij)= Max [Ei + tij]The computed values are put into the lower-left portion of each event.Backward pass method (For latest allowable time):In this method, the calculation begins from the last event L.The various steps are as follows:1. Set the latest occurrence time of the last event L which is equal to the earliest occurrence time of that event obtained from the forward pass method.i.e., Assume L = E for ending event.

2. Latest finish time for activity (i,j) equal to the latest event time of event j, i.e., LFij = Li

3. The latest starting time of activity (i,j) is the latest completion time of (i,j) minus the activity time i.e.LSij = LFij – tij= Li – tij4. Latest event time for the event i is the minimum of the latest start time of all activities originating from that event.Thus,Li = Minimum (LSij)= Min (LFij – tij)= Min (Lj – Lij)The computed values are put into the lower right portion of each event. Q7) Define the following terms: EST, EFT, LST, LFT, Free float, Independent float, and Interference float. A7) The terms can be defines as follows:

Earliest Start Time (EST):

The earliest possible time at which the event can occur. The EST also denotes the Earliest Start Time (EST) of activity as activities emanate from events. The EST of an activity is the time before which it cannot commence without affecting the immediately preceding activity.

Early Finish Time (EFT)

The earliest point in time when the scheduled activity can complete (based on preceding logic and constraints).

Latest Start Time (LST):

The latest time at which the event can take place. Also referred to as the Latest Start Time (LST) indicating the latest time at which an activity can begin without delaying the project completion time.

Late Finish Time (LFT)

The latest point in time when the scheduled activity can finish so as not to delay the project completion date or any constraint.

Free float

The term “free float” is used to describe the amount of time that spans from the completion of one previously scheduled activity and extends to the point at which the next scheduled activity is set to begin.

Independent float

An independent float is that part of the whole float which will delay the beginning of activity without affecting the float of the previous activity calculated for activity by subtracting tail event slack from the entire float.

Interfering float

Interference floats are part of the overall float and reduce the float for subsequent activities. This is the difference between the slowest end time of the activity in question and the earliest start time of the next activity, or zero, whichever is greater. Q8) Project consists of the following activities. Their sequence and duration are also given in the following table. Draw network and determine project duration, critical path. Also, calculate total float & free float for all the activities.

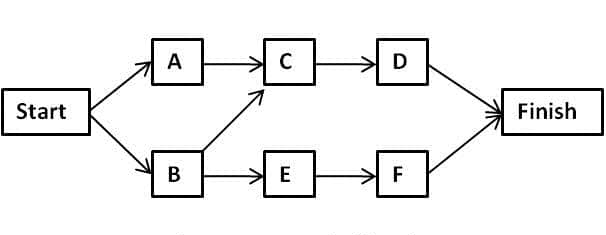
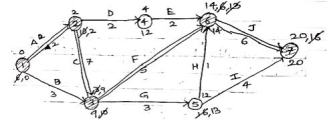
	A	B	C	D	E	F	G	H	I	J
Activity	1-2	1-3	2-3	2-4	4-6	3-6	3-5	5-6	5-7	6-7
Duration	2	3	7	2	2	5	3	1	4	6

A8) EFT=EST+d, LST=LFT-d (d=Duration)

Activity	Duration	EST	EFT	LST	LFT	T.F	F.F
A(1-2)	2	0	2	0	2	0	0
B(1-3)	3	0	3	6	9	6	6
C(2-3)	7	2	9	2	9	0	0
D(2-4)	2	2	4	10	12	8	0
E(4-6)	2	4	6	12	14	8	8
F(3-6)	5	9	14	9	14	0	0
G(3-5)	3	9	12	10	13	1	0
H(5-6)	1	12	13	13	14	1	1
I(5-7)	4	12	16	16	20	4	4
J(6-7)	6	14	20	14	20	0	0

Total float = LFT-EFT or LST-ESTFree float = TB−d−TA

enter image description here

Project duration = 20 DaysCritical path = 1-2-3-6-7i.e. A-C-F-J Q9) Define the terms: Normal Time, Normal Cost, Crash Time, Crash Cost of Activities. Cost Slope of an Activity, Direct costs, and Indirect costs. A9) The terms can be defined as:

Normal cost:

The normal cost is the lowest possible direct cost required to complete an activity.

Normal Time:

This is the time required when activities are performed in a normal way. It is usually the longest time for the project and entails money saving is there.

Crash Time:

This is the time in which the activity will be taken up on a crash basis for accomplishing. It indicates the shortest time for accomplishing the activity but money is not the criterion.

Crash Cost:

The cost involved when activity is performed on a crash basis without consideration of the costs involved. Time-saving is the main criterion.

Activity cost slope.

Activity cost slope is the rate of increase in the cost of activity per unit with a decrease in time. The cost slope indicates the additional cost incurred per unit of time saved in reducing the duration of an activity.

Direct costs:

It represents the expenditure which can be allocated to different activities in a project, like manpower, material, etc.

Indirect costs:

It represents the expenditure on those items which are shared by more than one activity and cannot be directly allocated to the individual activity of a project. Indirect costs of a project are those expenditures that cannot be apportioned or allocated to the individual activity. These include the expenditure related to the administration and establishment charges, overhead, supervision, loss of revenue, etc.

Q10) What are the steps in crashing a project?

A10) The process of Project Crashing is as follows:

1. Compute the crash cost per

period*. If crash costs are linear over time: 𝐶𝑟𝑎𝑠ℎ 𝐶𝑜𝑠𝑡 𝑃𝑒𝑟 𝑃𝑒𝑟𝑖𝑜𝑑 = 𝐶𝑟𝑎𝑠ℎ 𝐶𝑜𝑠𝑡 − 𝑁𝑜𝑟𝑚𝑎𝑙 𝐶𝑜𝑠𝑡 𝑁𝑜𝑟𝑚𝑎𝑙 𝑇𝑖𝑚𝑒 − 𝐶𝑟𝑎𝑠ℎ 𝑇𝑖𝑚𝑒

2. Find the critical path.

• Identify the critical activities using current activity times

3. Find the critical path activity with the lowest crash cost and crash this activity by 1-time unit

• E.g. Crash by 1 day, week, month

• Examine only critical path activities that can be crashed (i.e. max crash possible > 0)

• If there are multiple critical paths, crash multiple activities at the same time or crash one activity that is common to all the critical paths. Choose the strategy that gives the lowest overall cost.

4. Update all activity times. If the desired due date has been reached, stop. If not, return to Step 2.

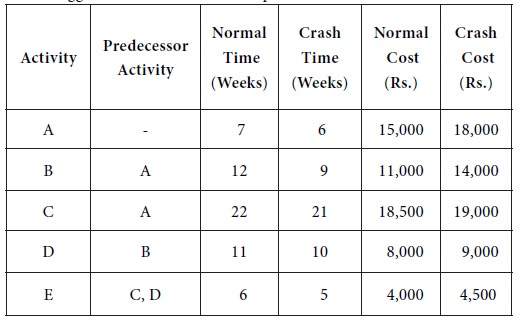
Q11) The management of a company is interested in crashing the following project by spending an additional amount not exceeding Rs. 2,000. Suggest how this can be accomplished.

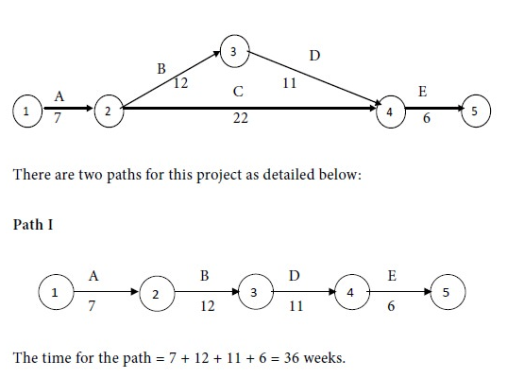
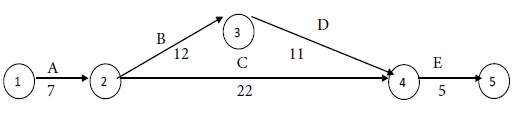
A11) We have the following network diagram for the given project with normal costs:

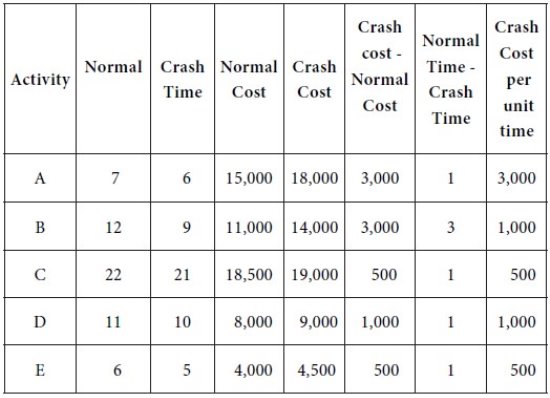
Therefore Path I is the critical path and the critical activities are A, B, D, and E. The non-critical activity is C.
The crash cost per unit time for the activities in the project is provided in the following table.

We have to choose one of the activities A, B, D, and E for crashing. The crash cost per unit time is as follows:

Rs. 3,000 for A; Rs. 1,000 for B; Rs. 1,000 for D; Rs. 500 for E.
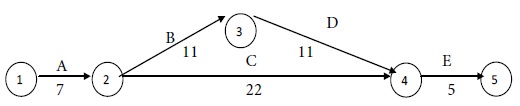
The least among them is Rs. 500. So we have to choose activity E for crashing. We reduce the time of E by one week by spending an extra amount of Rs. 500. After this step, we have the following network with the revised times for the activities:

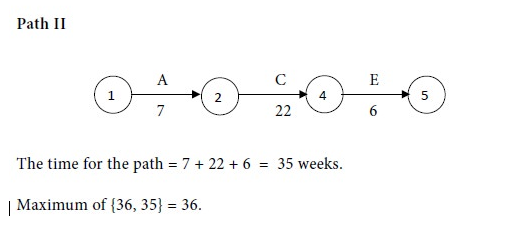
The revised time for Path I = 7 + 12 + 11 + 5 = 35 weeks.
The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {35, 34} = 35. Therefore Path I is the critical path and the critical activities are A, B, D, and E. The non-critical activity is C.
The time of E cannot be reduced further. So we cannot select it for crashing. Next B and have the smallest crash cost per unit time. Let us select B for crashing. Let us reduce the time of E by one week at an extra cost of Rs. 1,000.
After this step, we have the following network with the revised times for the activities:

The revised time for Path I = 7 + 11 + 11 + 5 = 34 weeks.
The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {34, 34} = 34.
Since both paths have equal times, both are critical paths. So, we can choose an activity for crashing from either of them depending on the least crash cost per unit time. In path I, the activities are A, B, D, and E. In path II, the activities are A, C, and E.
The crash cost per unit time is the least for activity C. So we select C for crashing. Reduce the time of C by one week at an extra cost of Rs. 500.
By the given condition, the extra amount cannot exceed Rs. 2,000.
Since this state has been met, we stop with this step.
Result: The following crashing scheme is suggested for the given project:
Reduce the time of E, B, and C by one week each.
Project time after crashing is 33 weeks.
Extra amount required = 500 + 1,000 + 500 = Rs. 2,000.

Q12) Differentiate between CPM and PERT.

A12) Difference between PERT and CPM :

S.No.	PERT	CPM
1.	PERT is that technique of project management that is used to manage uncertain (i.e., time is not known) activities of any project.	CPM is that technique of project management that is used to manage only certain (i.e., time is known) activities of any project.
2.	It is an event-oriented technique which means that network is constructed based on an event.	It is an activity-oriented technique which means that network is constructed based on activities.
3.	It is a probability model.	It is a deterministic model.
4.	It majorly focuses on time as meeting time target or estimation of percent completion is more important.	It majorly focuses on Time-cost trade-off as minimizing cost is more important.
5.	It is appropriate for high precision time estimation.	It is appropriate for reasonable time estimation.
6.	It has Non-repetitive nature of the job.	It has repetitive nature of the job.
7.	There is no chance of crashing as there is no certainty of time.	There may be crashing because of certain time boundation.
8.	It doesn’t use any dummy activities.	It uses dummy activities for representing the sequence of activities.
9.	It is suitable for projects which required research and development.	It is suitable for construction projects.

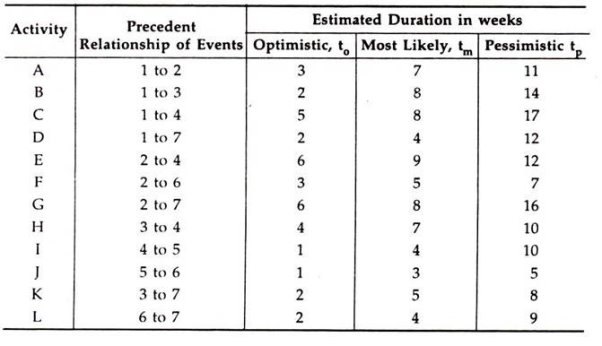
Q13) Following is a table of activities of a project with estimated optimistic, most likely, and pessimistic duration in weeks:

Considering the above details, we are to:(a) Draw project network;(b) Identify the critical path on the network;(c) Find the probability of completing the project in 32 weeks;(d) Find the estimated weeks of completion with a probability of 90%.

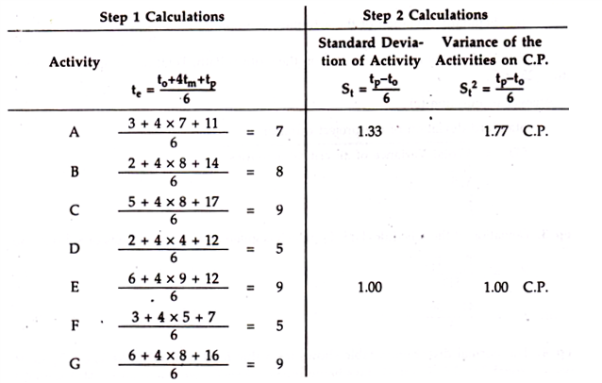
A13) Step 1:

To Calculate the Estimated time te per activity as per PERT:

... Standard Deviation SD = √6.83 = 2.61With the above te -s and the activities with the precedent relationship of events, we would like to prepare the network construction and then we find:1. ESTs of the events, starting with the event (1) as zero EST, then following the forward pass rule considering the longest EST when two or more activities converge to one event, till we reach the last event.2. LFTs of the events, starting with the last event, the last events LFT being the same as its EST. Then follow the ‘backward pass’ and find the LFT of the tail event (as LFT of head event, less tij) and, considering the shortest time units, when two or more activities emanate from one event.The solution to the question (a) and (b) drawing the project network and find the critical path:

Recapitulation of Time elements in network construction:(1) EST for event 4: activities C, E and H converge with C for 0 + 9 = 9 weeks, E for 7 + 9 = 16 weeks and H for 8 + 7 = 15 weeks. Therefore, we take the highest, i.e. 16.(2) LFT for event 2: activities E and F emanate from it coming backward from event 4, the LFT for 2 is 16 – 9 = 7 and, from event 6, the LFT for 2 is 23.5 – 5 = 18.5. Therefore, we take the lowest, i.e. 7.We find the events 1, 2, 4, 5, 6, and 7 are having EST = LFT and, as such, they are critical events and the double-line arrows shown in the network represent Critical Path with activities A, E, I, J and L; total project time being 28 weeks, i.e. TE is 28 weeks.The solution to question (c) to find the probability of completing the project in 32 weeks.Step 2:Calculations of duration:(a) Standard deviation of the activities duration St = tp-to /6 on the critical path marked CP.(b) Total of variances on Critical Path = 6-83(c) Standard Deviation of the Project Duration, = √6-83 = 2.61Step 3:Deviation of the scheduled date Ts (which is 32 weeks in question), in units of SD, is Z and the value of:Z= TS-TE/SD = 32 – 28/2.61 = 1.53Value of 1-53 per normal distribution table = 0-4370 = 0-44 (approx.).Step 4:We are to add 0-44 with 0-5; since 32 days is more than the mean project duration of 28 weeks, we are to add i.e. 0.50 + 0.44 = 0.94.... The probability to complete the project by 32 days is 94%.The solution for (d):Find the project duration with 90% probability. Ts is the unknown project schedule, it is more than TE as the probability of 90% is more than the probability of 50%. The value to adjust with 0.50 is 0.90 – 0.50 = 0.40. From the normal distribution table, we find the corresponding value of 0.40 is 1.28. In other words, the value of Z is 1.28.Therefore, putting the known values Z = TS-TE/SD =TS-28/2.61 = 1.28.or , Ts = 28 + 2.61 x 1.28= 28 + 3.34= 31.34 weeks.We can say with a 90% confidence level that the project can be completed by 31-34 weeks.

Sign Up