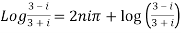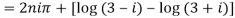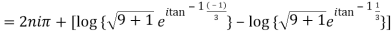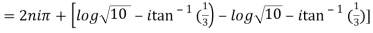Unit 2
Unit 2
Hyperbolic function and Logarithm of complex numbers
Question and answer
- Simplify
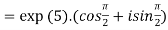
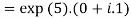
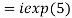
2. Find the value of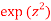 
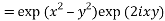
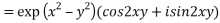
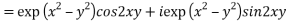
3. Expand the function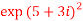 
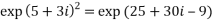
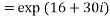
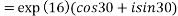
4. Find out the value of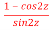 
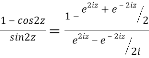
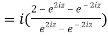
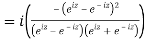
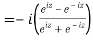
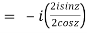
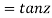
5. Prove that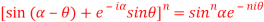 
LHS 
= 
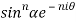
6. Solve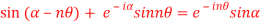 
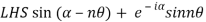
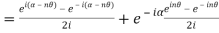
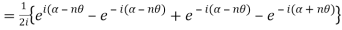
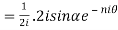
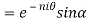
7. If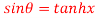
then prove that 
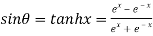……(i)
Squaring both sides
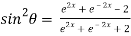
Now,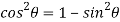 
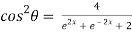
……(ii)
Dividing (i) by (ii)
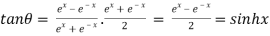
8. Prove that 
Let 
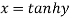
Squaring on both sides
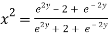
Again 
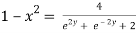
Taking square root on both side
Now, 
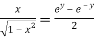
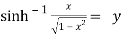
Hence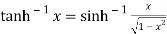 
9. Separate the real and imaginary part of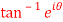 
Let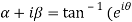 
)….(1)
…..(2)
On adding (1) and (2) we get
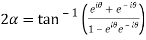
Subtracting (1) and(2) we get
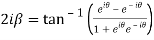
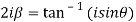
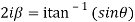
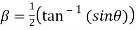
Which are the required real and imaginary parts.
10. Find the general value of 
The general value is
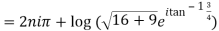
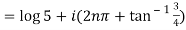
11. Separate the real and imaginary part of 
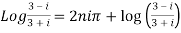
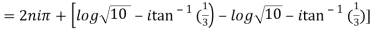
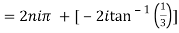
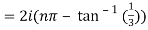
Unit 2
Hyperbolic function and Logarithm of complex numbers
Question and answer
- Simplify
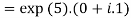
2. Find the value of 
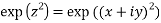
3. Expand the function 
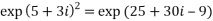
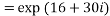
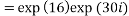
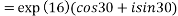
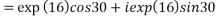
4. Find out the value of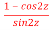 
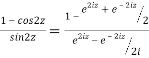
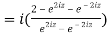
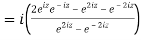
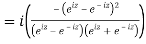
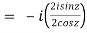
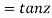
5. Prove that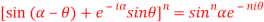 
LHS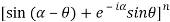 
= 
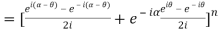
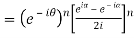
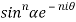
6. Solve 
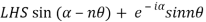
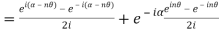
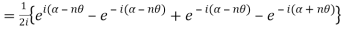
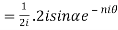
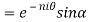
7. If
then prove that 
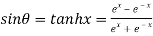……(i)
Squaring both sides
Now,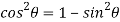 
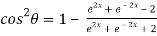
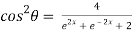
……(ii)
Dividing (i) by (ii)
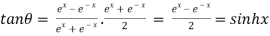
8. Prove that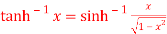 
Let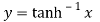 
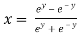
Squaring on both sides
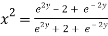
Again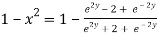 
Taking square root on both side
Now,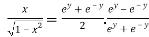 
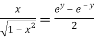
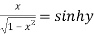
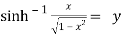
Hence 
9. Separate the real and imaginary part of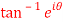 
Let 
)….(1)
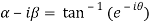…..(2)
On adding (1) and (2) we get
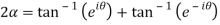
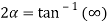
Subtracting (1) and(2) we get
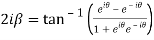
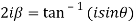
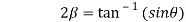
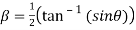
Which are the required real and imaginary parts.
10. Find the general value of 
The general value is
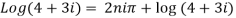
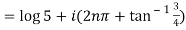
11. Separate the real and imaginary part of 
