Unit -3

Partial Differentiation

Question and answer

1. Find the value of

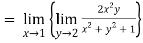
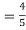
2.     Find the value of

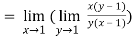
         As above value tend to infinite  as x and y approaches to 1

    Therefore using L-hospital rule

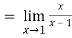
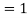
3.     If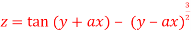

           Show that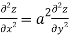

Given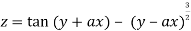 

Partially differentiating z with respect to x keeping y as constant

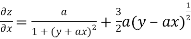
   Again partially differentiating z with respect to x keeping y as constant

Partially differentiating z with respect to y keeping x as constant

 Again partially differentiating z with respect to y keeping x as constant

From eq(i) and eq(ii) we conclude that

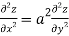
4.     If 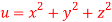where then find the value of ?

Given  

Where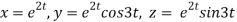 

By chain rule

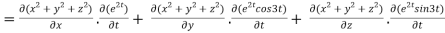
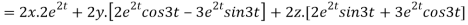
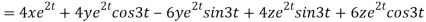
                          Now substituting the value of x ,y,z we get

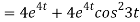                          -6

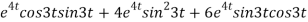
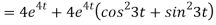
                          8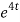

5.     If where the relation is .

Find the value of

Let the given relation is denoted by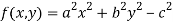

We know that

        Differentiating u with respect to x and using chain rule

6.     Show that

                              Given

    Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z

7.     If

                         Let

                        Thus u is an homogenous function of degree 2 in x and y

                               Therefore by Euler’s theorem

                                                  substituting the value of u

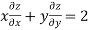
                                               Hence proved

8.     If

                Let

                Thus z is a homogenous function of degree 1 in x and y

            Therefore by deduction of Euler’s theorem

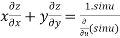
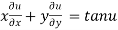
Hence proved

9.     If . Prove that

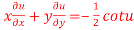
                              Let 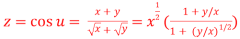    ….(i)

                   Thus  z is an homogenous equation of degree (1/2) in x and y

                    Therefore by deduction of Euler’s theorem

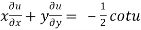
Hence proved 

10. If , prove that

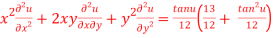
     Let

          Thus z is an homogenous equation of degree 1/12 in x and y

         Therefore by deduction of Euler’s theorem

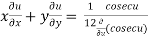
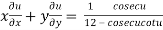
                                   ……(2)

                     Partially differentiating (2) with respect to x we get

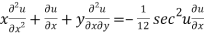
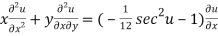                                    …..(3)

                     Partially differentiating (2) with respect to y we get

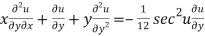
                                  …(4)

                   Multiplying x by (3)  and y by (4) and the on adding we get

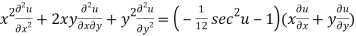
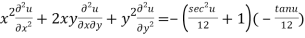                        {by using (1)}

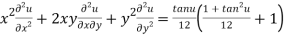
                       Hence proved.

Unit -3

Partial Differentiation

Question and answer

1. Find the value of

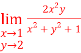
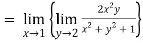
2.     Find the value of

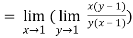
         As above value tend to infinite  as x and y approaches to 1

    Therefore using L-hospital rule

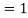
3.     If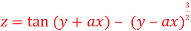

           Show that

Given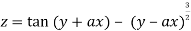 

Partially differentiating z with respect to x keeping y as constant

   Again partially differentiating z with respect to x keeping y as constant

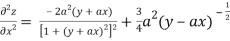
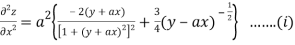
Partially differentiating z with respect to y keeping x as constant

 Again partially differentiating z with respect to y keeping x as constant

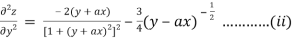
From eq(i) and eq(ii) we conclude that

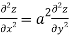
4.     If 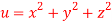where then find the value of ?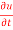

Given  

Where 

By chain rule

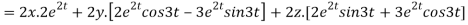
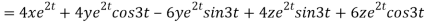
                          Now substituting the value of x ,y,z we get

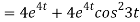                          -6

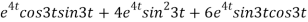
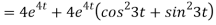
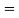                          8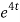

5.     If 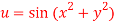where the relation is .

Find the value of

Let the given relation is denoted by

We know that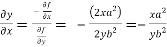

        Differentiating u with respect to x and using chain rule

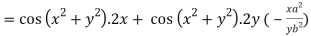
6.     Show that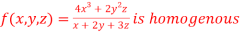

                              Given

    Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z

7.     If

                         Let

                        Thus u is an homogenous function of degree 2 in x and y

                               Therefore by Euler’s theorem

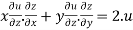
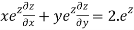                                                  substituting the value of u

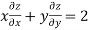
                                               Hence proved

8.     If

                Let

                Thus z is a homogenous function of degree 1 in x and y

            Therefore by deduction of Euler’s theorem

Hence proved

9.     If 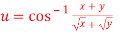. Prove that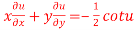

                              Let 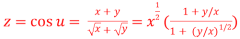    ….(i)

                   Thus  z is an homogenous equation of degree (1/2) in x and y

                    Therefore by deduction of Euler’s theorem

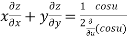
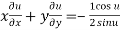
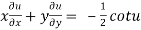
Hence proved 

10. If , prove that

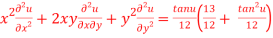
     Let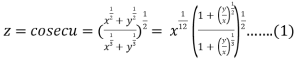

          Thus z is an homogenous equation of degree 1/12 in x and y

         Therefore by deduction of Euler’s theorem

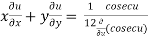
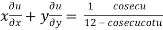
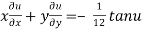                                   ……(2)

                     Partially differentiating (2) with respect to x we get

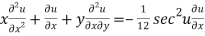
                                    …..(3)

                     Partially differentiating (2) with respect to y we get

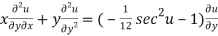                                  …(4)

                   Multiplying x by (3)  and y by (4) and the on adding we get

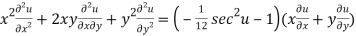
                        {by using (1)}

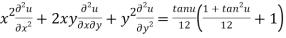
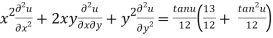
                       Hence proved.