Unit-5
Matrices
Question and Answer
- Let A =
 Find
Find  .
.
Then 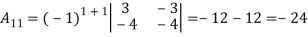

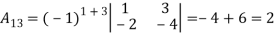


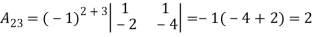


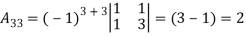

2. let A =  Find A-1
Find A-1
Then 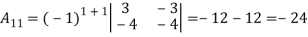
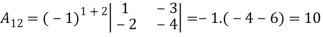
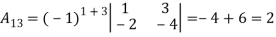
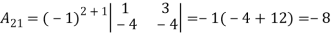


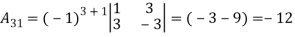
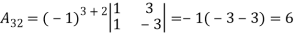

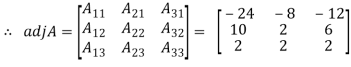
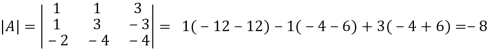
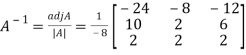
3. Express the matrix  as sum of a symmetric and skew symmetric matrix.
as sum of a symmetric and skew symmetric matrix.
Let A =  therefore A’ =
therefore A’ = 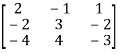
Suppose 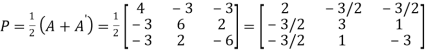
We calculate 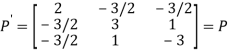
Hence P is the required symmetric matrix.
Again let 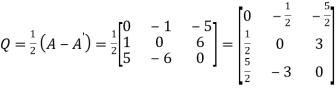
We find 
Hence Q is the required skew -symmetric matrix.
Now, we check

This implies that square matrix A can be represented as sum of symmetric and skew symmetric matrices.
4. Show that  is a Hermitian matrix.
is a Hermitian matrix.
Let A =  therefore A’ =
therefore A’ = 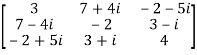
Now, 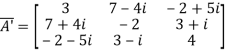
Here 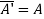
Hence given matrix is a Hermitian matrix
5. Show that 
Let A =  and then A’=
and then A’=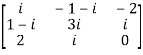

It is clear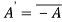 , hence the given matrix is skew-hermitian matrix.
, hence the given matrix is skew-hermitian matrix.
6. Express the matrix A as sum of hermitian and skew-hermitian matrix where 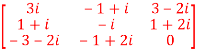
Let A =
Therefore 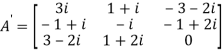 and
and 
Let 
Again 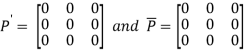
Hence P is a hermitian matrix.
Let 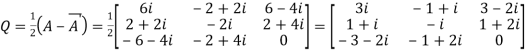
Again 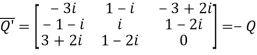
Hence Q is a skew- hermitian matrix.
We Check
P +Q=
Hence proved.
7. Prove that the following matrix is orthogonal:

Let A = 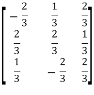 then A’=
then A’= 
Now, AA’=
Thus AA’=  = I
= I
Hence the matrix is orthogonal.
8. Prove that 
Let U =  therefore U’=
therefore U’= 
Also 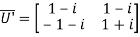
Now, UU’= 
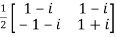
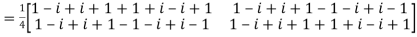
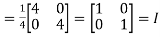
Hence the given matrix is a unitary matrix.
9. Find the rank of the following matrices?
Let A = 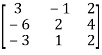
Applying 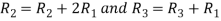
A 
Applying 
A 
Applying 
A 
Applying 
A 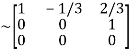
It is clear that minor of order 3 vanishes but minor of order 2 exists as 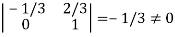
Hence rank of a given matrix A is 2 denoted by 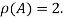
10. Reduce the matrix into normal form and find the rank of matrix:

Let A = 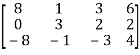
Apply 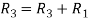

Apply 

Apply 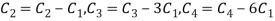

Apply 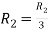

Apply 

Apply 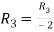
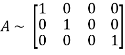
Apply 
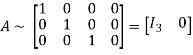
Hence the rank of the matrix is 3.
11. Find the non-singular matrices P and Q such that PAQ is in normal form:
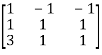
Let A = 
Also we know that A = A
A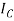 where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
 A
A
Apply 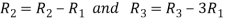
 A
A
Apply 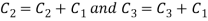
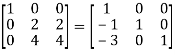 A
A
Apply 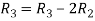
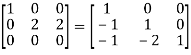 A
A
Apply 
 A
A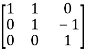
Apply 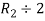
 A
A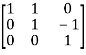
Or 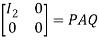 where P=
where P= , Q=
, Q=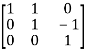
Hence the rank of matrix A is 2.
Unit-5
Matrices
Question and Answer
- Let A =
 Find
Find  .
.
Then 


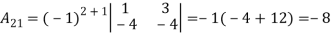
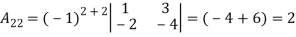


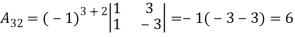

2. let A =  Find A-1
Find A-1
Then 

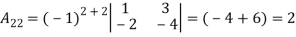
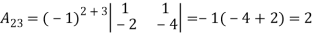
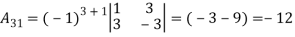
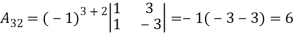



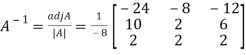
3. Express the matrix  as sum of a symmetric and skew symmetric matrix.
as sum of a symmetric and skew symmetric matrix.
Let A = 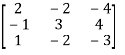 therefore A’ =
therefore A’ = 
Suppose 
We calculate 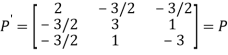
Hence P is the required symmetric matrix.
Again let 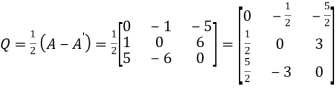
We find 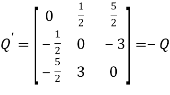
Hence Q is the required skew -symmetric matrix.
Now, we check

This implies that square matrix A can be represented as sum of symmetric and skew symmetric matrices.
4. Show that  is a Hermitian matrix.
is a Hermitian matrix.
Let A =  therefore A’ =
therefore A’ = 
Now, 
Here 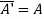
Hence given matrix is a Hermitian matrix
5. Show that 
Let A =  and then A’=
and then A’=
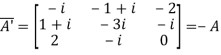
It is clear , hence the given matrix is skew-hermitian matrix.
, hence the given matrix is skew-hermitian matrix.
6. Express the matrix A as sum of hermitian and skew-hermitian matrix where 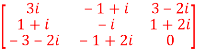
Let A =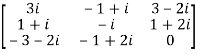
Therefore  and
and 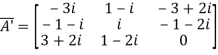
Let 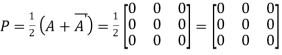
Again 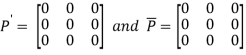
Hence P is a hermitian matrix.
Let 
Again 
Hence Q is a skew- hermitian matrix.
We Check
P +Q=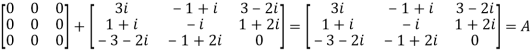
Hence proved.
7. Prove that the following matrix is orthogonal:

Let A =  then A’=
then A’= 
Now, AA’=
Thus AA’=  = I
= I
Hence the matrix is orthogonal.
8. Prove that 
Let U = 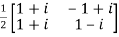 therefore U’=
therefore U’= 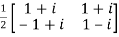
Also 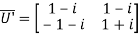
Now, UU’= 

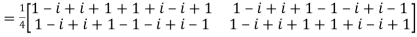

Hence the given matrix is a unitary matrix.
9. Find the rank of the following matrices?
Let A = 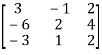
Applying 
A 
Applying 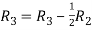
A 
Applying 
A 
Applying 
A 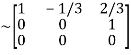
It is clear that minor of order 3 vanishes but minor of order 2 exists as 
Hence rank of a given matrix A is 2 denoted by 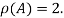
10. Reduce the matrix into normal form and find the rank of matrix:

Let A = 
Apply 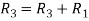

Apply 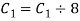

Apply 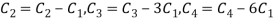

Apply 

Apply 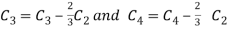

Apply 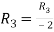

Apply 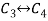

Hence the rank of the matrix is 3.
11. Find the non-singular matrices P and Q such that PAQ is in normal form:
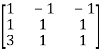
Let A = 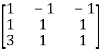
Also we know that A = A
A where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
 A
A
Apply 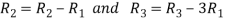
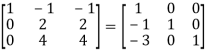 A
A
Apply 
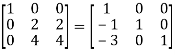 A
A
Apply 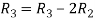
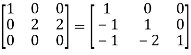 A
A
Apply 
 A
A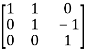
Apply 
 A
A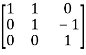
Or 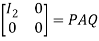 where P=
where P= , Q=
, Q=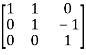
Hence the rank of matrix A is 2.

