Unit-6
Unit-6
Unit-6
Numerical solution of Transcendental Equations, System of Linear equations and Expansion of Functions
Question and answer
- Find a real root of the equation
 near
near , correct to three decimal place by the Regula Falsi method.
, correct to three decimal place by the Regula Falsi method.
Let 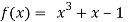
Now, 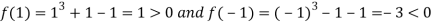
And also 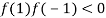
Hence the root of the equation 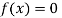 lies between
lies between 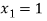 and
and 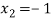 and so,
and so, 
By Regula Falsi Method
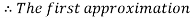

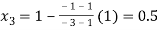
Now, 
So the root of the equation 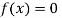 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 
By Regula Fasli Method
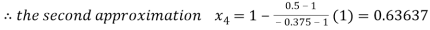
Now, 
So the root of the equation  lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 
By Regula Fasli Method
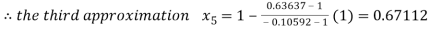
Now, 
So the root of the equation 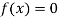 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 
By Regula Fasli Method
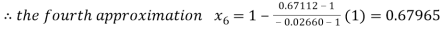
Now, 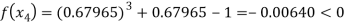
So the root of the equation  lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 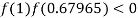
By Regula Fasli Method

Now, 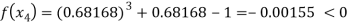
So the root of the equation  lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 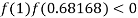
By Regula Fasli Method
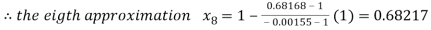
Now, 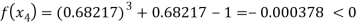
Hence the approximate root of the given equation near to 1 is 0.68217
2. Apply Regula Falsi Method to solve the equation

Let 
By hit and trail
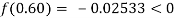
And 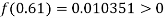
So the root of the equation lies between 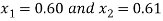 and also
and also 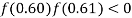
By Regula Falsi Mehtod

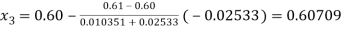
Now, 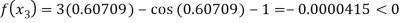
So, root of the equation 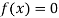 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 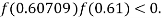
By Regula Falsi Method


Now, 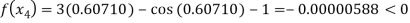
So, root of the equation 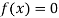 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 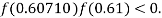
By Regula Falsi Method
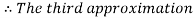

Hence the root of the given equation correct to five decimal place is 0.60710
3. Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: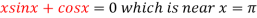 .
.
Given 


By Newton Raphson Method
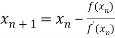
= 
=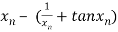
The initial approximation is 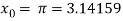 in radian.
in radian.
For n =0, the first approximation 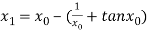

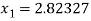
For n =1, the second approximation 
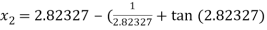
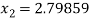
For n =2, the third approximation 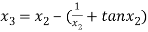
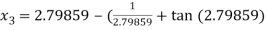

For n =3, the fourth approximation 
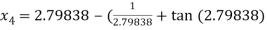

Hence the root of the given equation correct to five decimal place 2.79838.
4. Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places:  near to 4.5
near to 4.5
Let 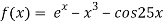

The initial approximation 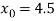
By Newton Raphson Method

For n =0, the first approximation 
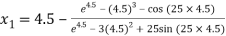
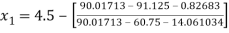
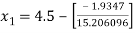

For n =1, the second approximation 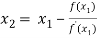
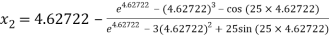
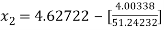

For n =2, the third approximation 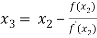

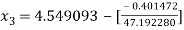

For n =3, the fourth approximation 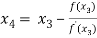
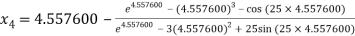

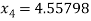
Hence the root of the equation correct to three decimal places is 4.5579
5. Use Jacobi’s method to solve the system of equations:

Since 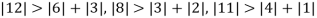
So, we express the unknown with large coefficient in terms of other coefficients.

 (1)
(1)
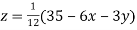
Let the initial approximation be 
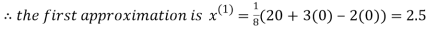
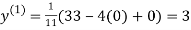
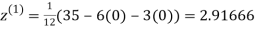

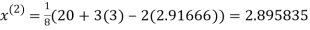
 2.35606
2.35606
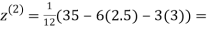 0.91666
0.91666
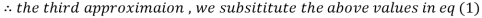
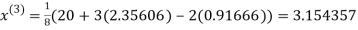

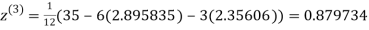
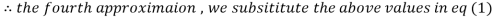
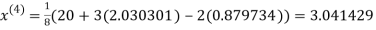
 1.932936
1.932936
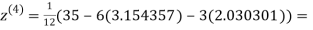 0.831912
0.831912

 3.016873
3.016873
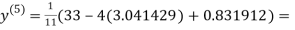 1.969654
1.969654

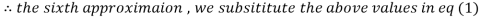
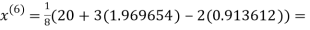 3.010217
3.010217
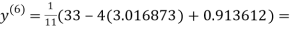 1.986010
1.986010


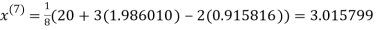
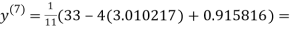 1.988631
1.988631
 0.915055
0.915055


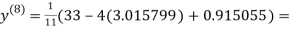 1.986532
1.986532
 0.911609
0.911609


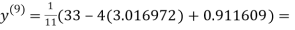 1.985792
1.985792
 0.911547
0.911547


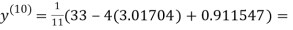 1.98576
1.98576
 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
6. Use Jacobi’s method to solve the system of the equations

Rewrite the given equations


 (1)
(1)
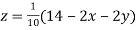
Let the initial approximation be 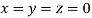
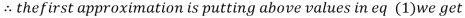
 1.2
1.2
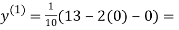 1.3
1.3
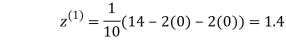
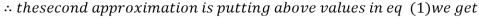
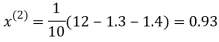

 0.9
0.9
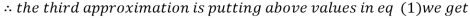

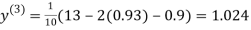
 1.03
1.03
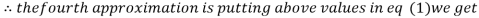
 0.9946
0.9946
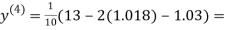 0.9934
0.9934
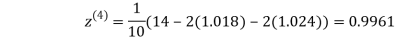
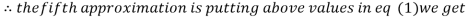
 1.0015
1.0015

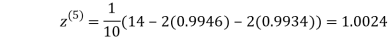
Hence the solution of the above equation correct to two decimal places is
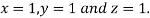
7. Use Gauss –Seidel Iteration method to solve the system of equations

Since 
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
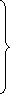

 (1)
(1)
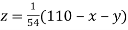
Let the initial approximation be 
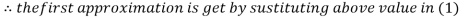
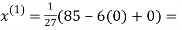 3.14814
3.14814
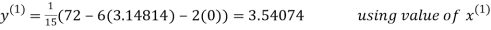
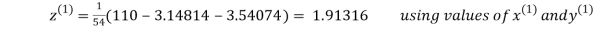
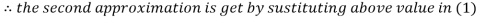
 2.43217
2.43217
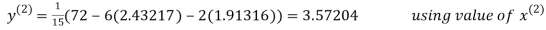
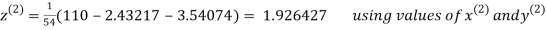
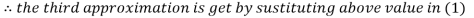
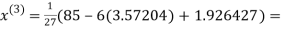 2.42571
2.42571



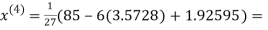 2.4260
2.4260
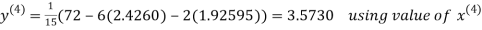

Hence the solution correct to three decimal places is
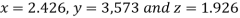
8. Solve the following equations by Gauss-Seidel Method



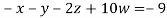
Rewrite the above system of equations
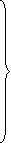
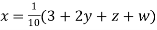

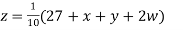 (1)
(1)
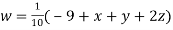
Let the initial approximation be 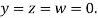
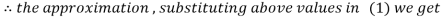



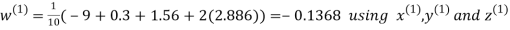
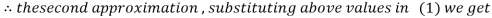
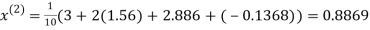

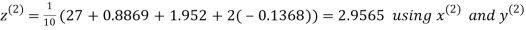


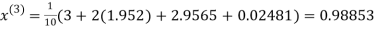
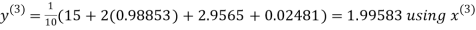

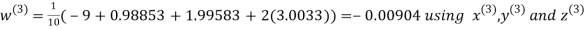
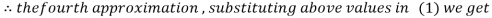

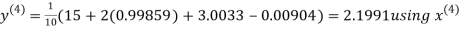

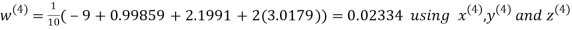
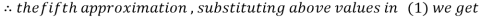
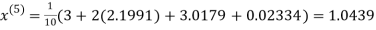

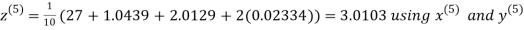
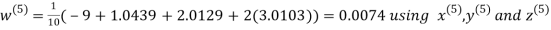
Hence the required solution is 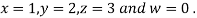
9. Expand  in power of
in power of 
Let 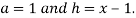
Also 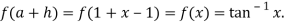
Differentiating f(x) with respect to x.

Again differentiating f(x) with respect to x.
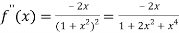
Again differentiating f(x) with respect to x.

Also the value of above functions at x=1 will be
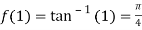
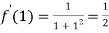

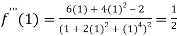
By Taylor’s theorem

On substituting above values we get


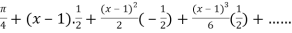
 =
= 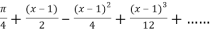
10. If 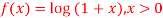 using Taylor’s theorem, show that for
using Taylor’s theorem, show that for  .
.
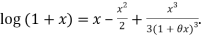
Deduce that 
Let 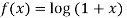 then
then 
Differentiating with respect to x.
 .Then
.Then 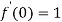
Again differentiating with respect to x.
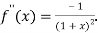 Then
Then 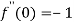
Again differentiating with respect to x.
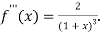 Then
Then 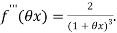
By Maclaurin’s theorem

Substituting the above values we get

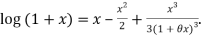
Since 

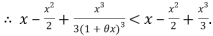
Hence 