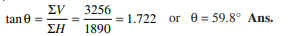Unit-1

Answer based question.

Q1) Two forces of 100 N and 150 N are acting simultaneously at a point. What is the resultant of these two forces, if the angle between them is 45°?

Ans. Given that

First force      F1=100N

Second force F2=150N

Angle              (θ) = 45°.

We know the resultant forces

Q2) Two forces act at an angle of 120°. The bigger force is of 40 N and the resultant is perpendicular to the smaller one. Find the smaller force

Ans. Angle between the forces ∠ AOC =120°, F1=40N and angle between resultant the forces F2 ∠BOC=90°                                                                                   

Let      F2= Smaller force in N

From the geometry of the figure we found that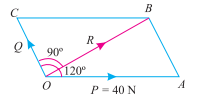

α = 120° – 90° = 30°

We know that

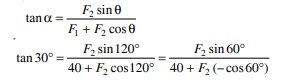
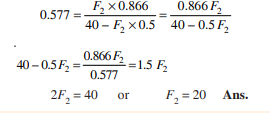
Q3) A machine component 1.5 m long and weight 1000 N is supported by two ropes AB and CD as shown in Fig. 2.2 given below.

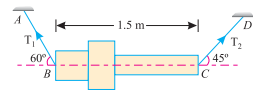
Calculate the tension given in the rope.

Ans. Weight of the component =1000N

Resolving the force horizontally and equating the same.

T1cos 60°=T2cos 45°

T1=1.414T2………(i)

And, now resolving the force vertically

T1sin60° + T2sin45°=1000N

(1.414T2)*0.866+T2*0.707=1000N

T2=518.1N

AndT1=732.6N Ans.

Q4) A system of forces is acting at the corners of a rectangular block as shown in figure.

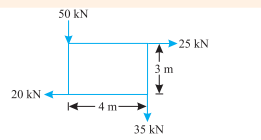
Determine the magnitude and direction of the resultant forces.

Ans. System of force

Magnitude of the resultant force

Resolving the force horizontally,

∑H=25-20=5KN

And, now resolving the force vertically

∑V= (-50) + (-35) = -85KN

Magnitude of the resultant force

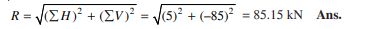
Q5) Determine the volume V and total surface area A of the solid generated by revolving the area shown through 180o about the z-axis.

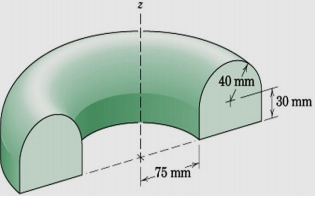
Ans. Let A1 be the surface area excluding the end surface and A2 be the surface area of the end surface.

Using Pappus theorem

A1 = π ̅L = π (75 + 40) (2×30 + 80 + (π × 40)) = 96000 mm^2

End areas A2 = 2 (π/2 × 40× 40 + 80 × 30)

=9830 mm^2

Total area A = A1+ A2 = 105800 mm^2

Again using Pappus theorem for revolution of plane areas:

V = π ̅r A = π (75 + 40) (30×80 + π ×1600/2) = 1775 × 10^6 mm^3

Q6) If FR is the net force of F1, F2, and F3, what is the magnitude of force F2 and x?

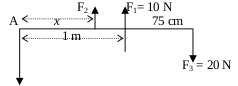
Ans. Force points to upward, signed negative and force points to downward, signed negative

∑F = 0

– FR + F1 + F2 – F3 = 0

– 40 + 10 + F2 – 20 = 0

F0=50N

Choose A as the axis of rotation.

τ1 = F1 l1 = (10 N)(1 m) = 10 Nm

τ2 = F2 x = (50) (x) = 50x Nm, τ 3 = F3 x = (20 N)(1.75 m) = -35 Nm

The net of moment of force :

∑τ = 0

10 + 50x – 35 = 0

50x – 25 = 0

50x = 25

x = 25/50

x = 0.5 m

Q7) A force of 15 N is applied perpendicular to the edge of a door 0.8 m wide as shown in Fig-(a). Find the moment of the force about the hinge.

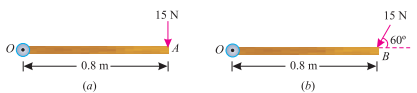
If this force is applied at an angle of 60° to the edge of the same door, as shown in Fig. 3.3 (b), find the moment of this force.

Ans. Given: Force applied (P) = 15 N and width of the door (l) = 0.8 m Moment when the force acts perpendicular to the door.

We know that the moment of the force about the hinge,

= P × l = 15 × 0.8 = 12.0 N-m Ans.

Moment when the force acts at an angle of 60° to the door

This part of the example may be solved either by finding out the perpendicular distance between the hinge and the line of action of the force as shown in Fig. 3.4 (a) or by finding out the vertical component of the force as shown in Fig. (b)

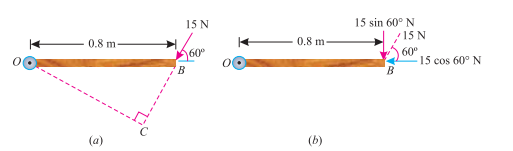
From the geometry of Fig. (a). We find that the perpendicular distance between the line of action of the force and hinge,

OC = OB sin 60° = 0.8 × 0.866 = 0.693 m

∴ Moment = 15 × 0.693 = 10.4 N-m Ans.

In the second case, we know that the vertical component of the force

= 15 sin 60° = 15 × 0.866 = 13.0 N

∴ Moment = 13 × 0.8 = 10.4 N-m Ans. Note.

Q8) A uniform plank ABC of weight 30 N and 2 m long is supported at one end A and at a point B 1.4 m from A as shown in Fig.

Find the maximum weight w. That can be placed at C, so that the plank does not topple.

Ans. Weight of the plank ABC = 30 N; Length of the plank ABC = 2 m and distance between end A and a point B on the plank (AB) = 1.4 m.

We know that weight of the plank (30 N) will act at its midpoint, as it is of uniform section. This point is at a distance of 1 m from A or 0.4 m from B as shown in the figure.

We also know that if the plank is not to topple, then the reaction at A should be zero for the maximum weight at C. Now taking moments about B and equating the same,

30 × 0.4 = W × 0.6

W =30 × 0.4/0.6

W=20N.

Q9) The forces 20 N, 30 N, 40 N, 50 N and 60 N are acting at one of the angular points of a regular hexagon, towards the other five angular points, taken in order. Find the magnitude and direction of the resultant force.

Ans. The system of forces as shown in figure.

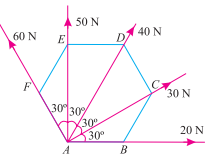
Magnitude of the resultant force

Resolving of the force horizontally

∑H=20cos 0° + 30cos 30° + 40cos 60° + 50cos 90° + 60cos 120° N

     = (20 × 1) + (30 × 0.866) + (40 × 0.5) + (50 × 0) + 60 (– 0.5) N

     =36N

And, now resolving of the force vertically

∑V = 20sin 0° + 30sin 30° + 40sin 60° + 50sin 90° + 60sin 120° N

      = (20 × 0) + (30 × 0.5) + (40 × 0.866) + (50 × 1) + (60 × 0.866) N

      =151.6N

We know that magnitude of the resultant force,

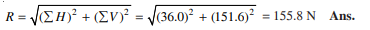
Direction of the resultant force,

We know that,

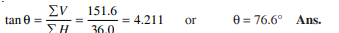
Q10) A horizontal line PQRS is 12 m long, where PQ = QR = RS = 4 m. Forces of 1000 N, 1500N, 1000 N and 500 N act at P, Q, R and S respectively with downward direction. The lines of action of these forces make angles of 90°,60°,45° and 30° respectively with PS. Find the magnitude, direction and position of the resultant force.

Ans. The system of given force is shown in figure.

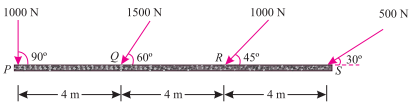
Magnitude of the resultant forces,

Resolving the for horizontally,

∑H = 1000cos 90° + 1500cos 60° + 1000cos 45° + 500cos 30° N

      = (1000 × 0) + (1500 × 0.5) + (1000 × 0.707) + (500 × 0.866) N

      =1890N

And, now resolving the force vertically,

∑V = 1000 sin 90° + 1500 sin 60° + 1000 sin 45° + 500 sin 30° N

                   = (1000 × 1.0) + (1500 × 0.866) + (1000 × 0.707) + (500 × 0.5) N

      =3256N

We know that magnitude of the resultant force,

Direction of the resultant forces,