Unit-2
Answer based question.
Q1) (a) Draw the free-body diagram of the beam. (b) Determine the tension in the rope and the reactions at B.
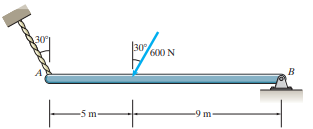
Ans. F.B.D of the beam
Let T be the tension in the rope
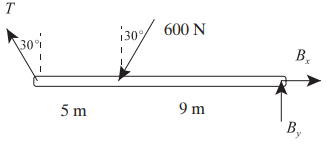
The equilibrium equations are:
∑Fx = - T sin 30° + (600 N) sin 30° + BX = 0
∑FY = T cos 30° + (600 N) cos 30° + BY = 0
∑MB = (600 N) cos 30° (9 m) - T cos 30° (4 m) = 0
I.e. T = 368 N, BX = 493 N, BY = 186N
Q2. The distance x = 9 m.
(a) Draw the free-body diagram of the beam.
(b) Determine the reactions at the supports.
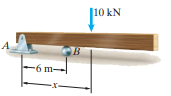
Ans. F.B.D of the diagram
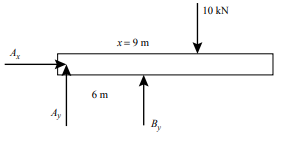
The equilibrium equations are:
∑Fx = AX =0
∑FY = AY + BY – 10 = 0
∑MA = BY (6) – 10(9) = 0
Solving this we find
AX =0, BY = 15 KN , AY = -5 KN
Q2) A simply supported beam AB of span 4.5 m is loaded as shown in Fig.
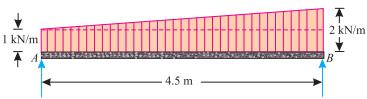
Find the support reactions at A and B.
Ans. Given: Span (l) = 4.5 m
Let RA = Reaction at A, and
RB = Reaction at B
For the sake of simplicity, we shall assume the uniformly varying load to be split up into (a) a uniformly distributed load of 1 KN/m over the entire span, and (b) triangular load of 0 at A to 1 KN/m at B.
We know that anticlockwise moment due to RB about A
= RB × l = RB × 4.5 = 4.5 RB KN-m ... (i)
And sum of clockwise moments due to uniformly varying load about A
= (1 × 4.5 × 2.25) + (2.25 × 3) = 16.875 KN-m ... (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii)
4.5 RB = 16.875
RB =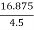 
RB = 3.75 KN
And RA = (1
4.5) + (4.5 
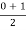) – 3.75 = 3 KN
Q4. A simply supported beam AB of 6 m span is subjected to loading as shown in Fig.
Find graphically or otherwise, the support reactions at A and B.
Ans. Given: Span (l) = 6 m
Let RA = Reaction at A, and
RB = Reaction at B
We know that anticlockwise moment due to RB about A
= RB × l = RB × 6 = 6 RB KN-m ……………….. (i)
And sum of clockwise moments due to loads about A
= (4×1) + (2×1) 1.5 + (4×2) + 
×3×5 = 30 KN-m. …. (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii),
6 RB = 30
RB = 5 KN
And RA = (4 + 2 + 4 + 3) – 5 = 8 KN
Q5. A beam AB of span 3m, overhanging on both sides is loaded as shown in Fig.
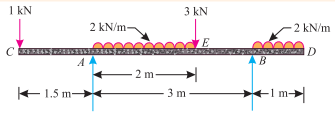
Determine the reaction at the support A and B.
Ans. Given: Span (l) = 3 m
Let RA = Reaction at A, and
RB = Reaction at B
We know that anticlockwise moment due to RB and load at C about A
= RB × l + (1 × 1.5) = RB× 3 + (1 × 1.5) = 3RB + 1.5 KN ... (i)
And sum of clockwise moments due to loads about A
= (2 × 2) 1 + (3 × 2) + (1 × 1) 3.5 = 13.5 KN-m ... (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii),
3RB + 1.5 =13.5
RB = 4 KN
AndRA = 1 + (2 × 2) + 3 + (1 × 1) – 4 = 5 KN
Q6. A beam AB 5 m long supported on two intermediate supports 3 m a part carries a uniformly distributed load of 0.6 KN/m. The beam also carries two concentrated loads of 3 KN at left hand end A, and 5 KN at the right hand end B as shown in Fig.
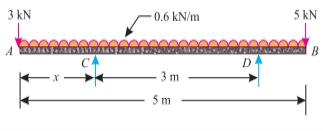
Determine the location of the two supports, so that both the reactions are equal.
Ans. Given: Length of the beam AB (L) = 5 m and span (l) = 3 m.
Let RC =Reaction at C,
RD =Reaction at D, and
x =Distance of the support C from the left hand end
We know that total load on the beam
=3 + (0.6 × 5) + 5 = 11 KN
Since the reactions RC and RD are equal, therefore reaction at support
= 
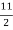= 5.5 KN
We know that anticlockwise moment due to RC and RD about A
= 5.5 × x + 5.5 (x + 3) = 5.5 x + 5.5 x + 16.5 KN-m
=11x + 16.5 KN-m ... (i)
And sum of clockwise moment due to loads about A
= (0.6 × 5) 2.5 + 5 × 5 = 32.5 KN-m ... (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii)
11 x + 16.5 = 32.5 or 11 x = 16
x= 
= 1.45m
It is thus obvious that the first support will be located at distance of 1.45m from A and second support at a distance of 1.45 + 3 = 4.45 m from A.
Q3) A simply supported beam AB of span 5 m is loaded as shown in Fig. 12.7. Find the reactions at A and B.
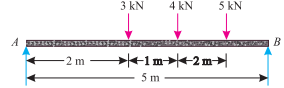
Ans. Given: Span (l) = 5 m
Let RA = Reaction at A, and
RB = Reaction at B
We know that anticlockwise moment due to RB about A
= RB × l = RB × 5 = 5 RB KN-m …………………………… (i)
And sum of the clockwise moments about A,
= (3 × 2) + (4 × 3) + (5 × 4) = 38 KN-m ………………. (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii),
5 RB = 38
RB = 7.6 KN
And RA = (3 + 4 + 5) – 7.6 = 4.4 KN
Q8. A beam AB of 6 m span is loaded as shown in Fig.
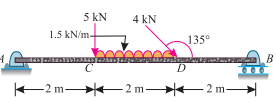
Ans. Given: Span (l) = 5 m
Let RA = Reaction at A, and
RB = Reaction at B
Resolving the 4 KN load at D vertically
= 4 sin 45° = 4 × 0.707 = 2.83 KN
And now resolving it horizontally
= 4 cos 45° = 4 × 0·707 = 2·83 KN
We know that anticlockwise moment due to RB about A
= RB × 6 = 6 RB KN-m ………………………….. (i)
And sum of clockwise moments due to loads about A
= (5 × 2) + (1.5 × 2) 3 + 2.83 × 4 = 30.3 KN-m ……….. (ii)
Now equating the anticlockwise and clockwise moments in (i) and (ii)
6 RB = 30.3
RB = 5.05 KN
We know that vertical component of the reaction
RA = [5 + (1.5 × 2) + 2.83] – 5.05 = 5.78 KN
Reaction at A,
RA = 
= 6.44 KN
= Angle, which the reaction at A makes with vertical
Tan 
= 
or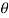 
=26.1°
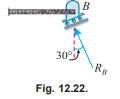
Q9. A beam AB 8.5 m long is hinged at A and supported on rollers over a smooth surface inclined at 30° to the horizontal at B. The beam is loaded as shown in Fig
Determine the reactions at A and B
Ans. Given: Span (l) =8.5 m
Let RA = Reaction at A, and
RB = Reaction at B
We know that as the beam is supported on rollers at B, therefore the reaction at this end will be normal to the support i.e. inclined at an angle of 30° with the vertical (because the support is inclined at 30° with the horizontal) as shown in Fig. 12.22. Moreover, as the beam is hinged at A, therefore the reaction at this end will be the resultant of vertical and horizontal forces, and thus will be inclined with the vertical.
Resolving the 4 KN load at D vertically
= 4 sin 45° = 4 × 0.707 = 2.83 KN
And now resolving it horizontally
= 4 cos 45° = 4 × 0.707 = 2.83 KN
We know vertical component of reaction RB
= RB cos 30° = RB × 0.866 = 0.866 RB
And anticlockwise moment due to vertical component of reaction RB about A
= 0.866 RB × 8.5 = 7.361 RB …………………………………….. (i)
We also know that sum of clockwise moments due to loads about A
= (5 × 2) + (2.83 × 4) + (5 × 7) = 56.32 KN-m ……………... (ii)
Now equating anticlockwise and clockwise moments given in (i) and (ii)
7.361 RB = 56.32
RB = 7.56KN
We know that vertical component of the reaction RB
= 0.866 RB = 0.866 × 7.65 = 6.625 KN
And horizontal component of reaction
RB = RB sin 30° = 7.65 × 0.5 = 3.825 KN
∴ Vertical component of reaction
RA = (5 + 2.83 + 5) – 6.625 = 6.205 KN
And horizontal component of reaction
RA = 3.825 – 2.83 = 0.995 KN
∴RA =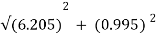 
=6.28 KN
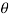= Angle, which the reaction at A makes with vertical
Tan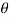 
= 
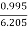or 
=9.1°
Q10. A beam has hinged support at A and roller support at B as shown in Fig.
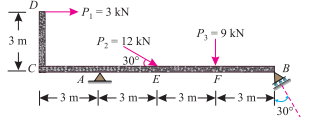
The beam is subjected to loads as shown. Determine analytically the reactions at A and B.
Ans. Given: Span (l) =9 m
Let RA = Reaction at A, and
RB = Reaction at B
Resolving the 12 KN load at E vertically
= 12 sin 30° = 12 × 0.5 = 6 KN
And now resolving it horizontally
= 12 cos 30° = 12 × 0.866 = 10.4 KN
We know that vertical component of reaction RB.
= RB cos 30° = RB × 0.866 = 0.866 RB
And anticlockwise moment due to vertical component of reaction RB about A
= 0.866 RB × 9 = 7.794 RB …………………………………. (i)
We also know that sum of clockwise moments due to loads about A
= (6 × 3) + (9 × 6) + (3 × 3) = 81 KN-m ………………….. (ii)
Now equating the anticlockwise and clockwise moments given in (i) and (ii),
7.694 RB = 81
RB = 10.4 KN
We know that vertical component of the reaction RB
= 0.866 RB = 0.866 × 10.4 = 9.0 KN
And horizontal component of reaction RB
= RB sin 30° = 10.4 × 0.5 = 5.2 KN
Vertical component of reaction
RA = (6 + 9) – 9 = 6 KN
And horizontal component of reaction
RA = (3 + 10.4) – 5.2 = 8.2 KN
OrRA =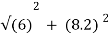 
= 10.26 KN
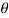= Angle, which the reaction at A makes with vertical
Tan 
= 
or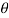 
=53.8°
