Unit 3
Unit 3
Unit 3
Answer based question.
Q1 Two blocks A and B of weights 5 KN and 7 KN respectively are in equilibrium position as shown in Fig.
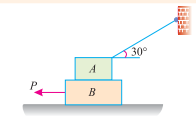
If the coefficient of friction between the two blocks as well as the block B and the floor is 0.4, find the force (P) required moving the block B.
Sol. Given: Weight of block A (WA) = 5 KN; Weight of block B (WB) = 7 KN and coefficient of friction ( ) = 0.4.
) = 0.4.
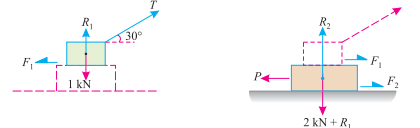
(i) Block A(ii) Block B
The forces acting on the two blocks A and B are shown in Fig. (A) and (B) respectively. First of all, consider the forms acting in the block A.
Resolving the force vertically
R1 + T sin 30° = 5
T sin30° = 5- R1……………………………… (i)
And resolving the force horizontally
Tcos30° = F1 = R1 =0.4 R1 ............................... (ii)
R1 =0.4 R1 ............................... (ii)
Dividing equation (i) by (ii)
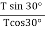 =
=  or tan30° =
or tan30° =
0.5774 = 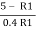 or 0.5774
or 0.5774  0.4R1 = 5- R1
0.4R1 = 5- R1
R1 = 4.06 KN
And F1 = 0.4  4.06 = 1.62 KN
4.06 = 1.62 KN
Now consider the block B. A little consideration will show that the downward force of the block (A) (equal to R1) will also act along with the weight of the block B.
Resolving the force vertically
R2 = 7 + R1 = 7 + 0.85 = 7.85 KN
F2 = 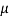 R2 = 0.4
R2 = 0.4  7.85 = 3.14 KN
7.85 = 3.14 KN
Now resolving the force horizontally
P = F1 + F2 = 1.62 + 3.14 = 4.76 KN
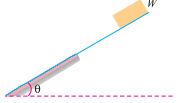
Q2. A body of weight 500 N is laying on a rough plane inclined at an angle of 25° with the horizontal. It is supported by an effort (P) parallel to the plane as shown in Fig.

Determine the minimum and maximum values of P, for which the equilibrium can exist, if the angle of friction is 20°.
Sol. Given: Weight of the body (W) = 500 N; Angle at which plane is inclined (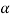 ) = 25° and angle of friction (
) = 25° and angle of friction ( ) = 20°.
) = 20°.
Minimum value of P
We know that for the minimum value of P, the body is at the point of sliding downwards. We also know that when the body is at the point of sliding downwards, then the force.
P1 =W 
 = 500
= 500 
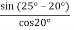 = 4.64 N
= 4.64 N
Maximum value of P
We know that for the maximum value of P, the body is at the point of sliding upwards. We also know that when the body is at the point of sliding upwards, then the force
P2 = W 
 = 500
= 500 
 = 376.2 N
= 376.2 N
Q3. An inclined plane as shown in Fig. Is used to unload slowly a body weighing 400 N from a truck 1.2 m high into the ground.

The coefficient of friction between the underside of the body and the plank is 0.3. State whether it is necessary to push the body down the plane or hold it back from sliding down. What minimum force is required parallel to the plane for this purpose?
Sol. Given: Weight of the body (W) = 400 N and coefficient of friction ( ) = 0.3. Whether it is necessary to push the body down the plane or hold it back from sliding down.
) = 0.3. Whether it is necessary to push the body down the plane or hold it back from sliding down.
We know that
Tan =
=  = 0.5 or
= 0.5 or 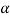 = 26.5°
= 26.5°
And normal reaction, R = W cos  = 400 cos 26.5° N
= 400 cos 26.5° N
= 400 × 0.8949 = 357.9 N
∴ Force of friction
F = 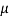 R = 0.3 × 357.9 = 107.3 N ...(i)
R = 0.3 × 357.9 = 107.3 N ...(i)
Now resolving the 400 N force along the plane
= 400 sin = 400 × sin 26.5° N
= 400 × sin 26.5° N
= 400 × 0.4462 = 178.5 N….(ii)
We know that as the force along the plane (which is responsible for sliding the body) is more than the force of friction, therefore the body will slide down. Or in other words, it is not necessary to push the body down the plane; rather it is necessary to hold it back from sliding down.
Minimum force required parallel to the plane
We know that the minimum force required parallel to the plane to hold the body back,
P = 178.5 – 107.3 = 71.2 N
Q4. An effort of 200 N is required just to move a certain body up an inclined plane of angle 15° the force acting parallel to the plane. If the angle of inclination of the plane is made 20° the effort required, again applied parallel to the plane, is found to be 230 N. Find the weight of the body and the coefficient of friction.
Sol. Given: First case: When effort (P1) = 200 N, then angle of inclination ( 1) = 15° and second case: When effort (P2) = 230 N, then angle of inclination (
1) = 15° and second case: When effort (P2) = 230 N, then angle of inclination ( 2) = 20°.
2) = 20°.
Let  = Coefficient of friction,
= Coefficient of friction,
W = Weight of the body,
R = Normal reaction, and
F = Force of friction.
First of all, consider the body lying on a plane inclined at an angle of 15° with the horizontal and subjected to an effort of 200 N as shown in Fig. (a).
Resolving the forces at right angles to the plane,
R1 = W cos 15° ... (i)
And now resolving the forces along the plane,
200 = F1 + W sin 15° = 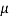 .R1 + W sin 15 °
.R1 + W sin 15 °
=  W cos 15° + W sin 15°
W cos 15° + W sin 15°
= W (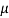 cos 15° + sin 15°)… (ii)
cos 15° + sin 15°)… (ii)
Now consider the body lying on a plane inclined at an angle of 20° with the horizontal and subjected to an effort of 230 N shown in Fig. (b).
Resolving the forces at right angles to the plane,
R2 = W cos 20°……… (ii)
And now resolving the forces along the plane,
230 = F22+ W sin 20° =  R2 + W sin 20°
R2 + W sin 20°
= W (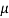 cos 20° + sin 20°) ……. (iv)
cos 20° + sin 20°) ……. (iv)
Coefficient of friction
Dividing equation (iv) by (ii)
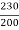 =
=
230 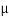 cos 15° + 230 sin 15° = 200
cos 15° + 230 sin 15° = 200 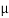 cos 20° + 200 sin 20°
cos 20° + 200 sin 20°
230 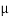 cos 15° – 200
cos 15° – 200 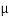 cos 20° = 200 sin 20° – 230 sin 15°
cos 20° = 200 sin 20° – 230 sin 15°
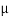 =0.259
=0.259
Weight of the body
Substituting the value of 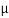 in equation (ii)
in equation (ii)
200 = W (0.259 cos 15° + sin 15°)
= W (0.259 × 0.9659 + 0.2588) = 0.509 W
W = 392.9 N
Q5. A load of 1.5 KN, resting on an inclined rough plane, can be moved up the plane by a force of 2 KN applied horizontally or by a force 1.25 KN applied parallel to the plane. Find the inclination of the plane and the coefficient of friction.
Sol. Given: Load (W) = 1.5 KN; Horizontal effort (P1) = 2 KN and effort parallel to the inclined plane (P2) = 1.25 KN.
Inclination of the plane,
Let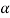 = Inclination of the plane, and
= Inclination of the plane, and
 = Angle of friction.
= Angle of friction.

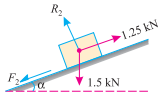
(a) Horizontal force(b) Force parallel to plane
First of all, consider the load of 1.5 KN subjected to a horizontal force of 2 KN as shown in figure. We know that when the force is applied horizontally, then the magnitude of the force, which can move the load up the plane.
P = W tan (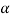 +
+ )
)
2 = 1.5 tan ( +
+ )
)
Tan (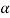 +
+ ) =1.33 or (
) =1.33 or (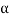 +
+ ) =53.1°
) =53.1°
Now consider the load of 1.5 KN subjected to a force of 1.25 KN along the plane as shown in figure. We Know that when the force is applied parallel to the plane, then the magnitude of the force, which can move the load up the plane,
P = W 

Or 1.25= 1.5 

Cos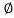 =0.96
=0.96
 = 16.3°
= 16.3°
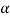 = 53.1° – 16.3° = 36.8°
= 53.1° – 16.3° = 36.8°
Coefficient of friction
We know that the coefficient of friction,
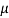 = tan
= tan  = tan 16.3° = 0.292
= tan 16.3° = 0.292
Q6. Two blocks A and B, connected by a horizontal rod and frictionless hinges are supported on two rough planes as shown in figure.
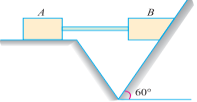
The coefficients of friction are 0.3 between block A and the horizontal surface, and 0.4 between block B and the inclined surface. If the block B weighs 100 N, what is the smallest weight of block A that will hold the system in equilibrium?
Sol. Given: Coefficient of friction between block A and horizontal surface (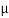 A) = 0.3; Coefficient of friction between block B and inclined surface (
A) = 0.3; Coefficient of friction between block B and inclined surface (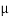 B) = 0.4 and weight of block B (WB) = 100 N.
B) = 0.4 and weight of block B (WB) = 100 N.
Let WA = Smallest weight of block A.
We know that force of friction of block A, which is acting horizontally on the block B
P =  A WA = 0.3 × WA = 0.3 WA
A WA = 0.3 × WA = 0.3 WA
And angle of friction of block B
Tan  =
=  B = 0.4 or
B = 0.4 or  = 21.8°
= 21.8°
We also know that the smallest force, which will hold the system in equilibrium (or will prevent the block B from sliding downwards),
P = WB tan ( –
–  ) = 100 tan (60° – 21.8°)
) = 100 tan (60° – 21.8°)
Or 0.3 WA = 100 tan 38.2° = 100 × 0.7869 = 78.69
WA = 262.3 N
Q7. Find the force required to move a load of 300 N up a rough plane, the force being applied parallel to the plane. The inclination of the plane is such that when the same load is kept on a perfectly smooth plane inclined at the same angle, a force of 60 N applied at an inclination of 30° to the plane, keeps the same load in equilibrium.
Assume coefficient of friction between the rough plane and the load to be equal to 0.3
Sol. 1st case
Given: In this case load (P) = 60 N; Angle (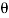 ) = 30° and force of friction F = 0 (because of smooth plane). Resolving the forces along the inclined plane,
) = 30° and force of friction F = 0 (because of smooth plane). Resolving the forces along the inclined plane,
60 cos 30° = 300 sin 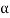
Sin  = 0.1732 or
= 0.1732 or 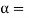 10°
10°
2nd case
Given: In this case, coefficient of friction ( ) = 0.3 = tan
) = 0.3 = tan  or
or  = 16.7°
= 16.7°
Let P = Force required to move the load up the plane,
R = Normal reaction, and
F = Force of friction equal to 0.3 R.
Resolving the forces along the plane,
P = F + 300 sin 10° = 0.3 R + (300 × 0.1732) = 0.3 R + 51.96 N …. (i)
And now resolving the forces at right angles to the plane,
R = 300 cos 10° = 300 × 0.9849 = 295.5 N…. (ii)
Substituting the value of R in equation (i),
P = (0.3 × 295.5) + 51.96 = 140.7 N
Q8. The upper half of an inclined having inclination 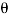 with the horizontal is smooth, while the lower half in rough as shown in figure.
with the horizontal is smooth, while the lower half in rough as shown in figure.
If a body of weight W slides down from rest at the top, again comes to rest at the bottom of the plane, and then determine the value of coefficient of friction for the lower half of the plane.
Sol. Given: Angle of inclination = and weight of the body = W
and weight of the body = W
Let  = Coefficient of friction for the lower half of the inclined alone
= Coefficient of friction for the lower half of the inclined alone
We know that acceleration on the smooth surface of the plane
= g sin  ……………. (i)
……………. (i)
And retardation on the rough surface of the plane
= – g (sin 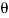 –
–  cos
cos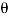 )
)
= g (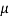 cos
cos 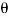 – sin
– sin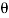 ) …………….. (ii)
) …………….. (ii)
Since body starts from rest at the top comes to rest at the bottom of therefore acceleration on the smooth surface is equal to retardation on the rough surface.
g sin 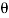 = g (
= g (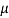 cos
cos 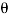 – sin
– sin 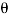 ) or sin
) or sin  =
= 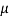 cos
cos 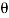 – sin
– sin 
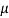 Cos
Cos  = 2 sin
= 2 sin 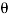 or
or  = 2 tan
= 2 tan 
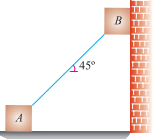
Q9. Two identical blocks of weight W are supported by a rod inclined at 45° with the horizontal as shown in figure.
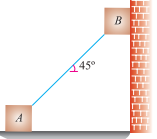
If both the blocks are in limiting equilibrium, find the coefficient of friction (μ), assuming it to be the same at floor as well as at wall.
Sol. Given: Weight of blocks A and B = W and inclination of rod with the horizontal (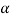 ) = 45°.
) = 45°.
Let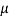 = Coefficient of friction, and
= Coefficient of friction, and
l = Length of the rod.
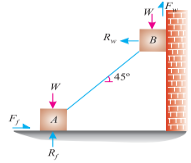
The forces acting on both the blocks are shown in Fig.
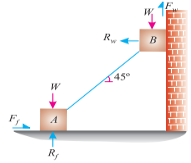
Resolving the forces vertically.
FW + RF = 2W
 RW + RF = 2W…………… (i)
RW + RF = 2W…………… (i)
And now resolving the forces horizontally
RW = FF = 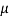 RF…………… (ii)
RF…………… (ii)
Now substituting this value of RW in equation (i)
 (
( RF) + RF = 2W
RF) + RF = 2W
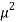 RF + RF = 2W
RF + RF = 2W
RF = 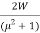 …………… (iii)
…………… (iii)
And now substituting this value of RF in equation (ii),
RW = 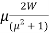
Taking moments of the forces about the block A and equating the same,
RW × l cos 45° + FW × l cos 45° = W × l cos 45°
RW + FW = W
RW (1 +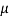 ) = W
) = W
Substituting the value of RW from equation (iv),
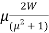 (1 +
(1 + ) = W
) = W
 + 2
+ 2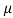 – 1 = 0
– 1 = 0
Solving it as quadratic equation for 
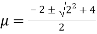 = 0.414
= 0.414
Q10. A uniform ladder of weight of 300 N rests against a smooth vertical wall a rough horizontal floor making at angle 60 with the horizontal. Find the force of friction at floor.
Sol. Draw free body diagram of ladder AB and apply condition of equilibrium.
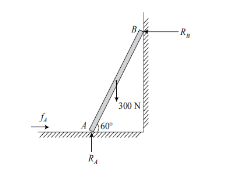
As the wall is smooth, 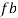 = 0
= 0
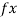 = 0
= 0
FA = RA
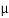 RA = RB
RA = RB
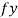 = 0
= 0
RA = W = 300N
FA = 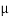 RA = 300
RA = 300
Assume µ = 0.3 between ladder and floor
The force of friction,
FA = 90 N
Unit 3
Unit 3
Answer based question.
Q1 Two blocks A and B of weights 5 KN and 7 KN respectively are in equilibrium position as shown in Fig.
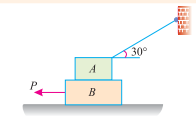
If the coefficient of friction between the two blocks as well as the block B and the floor is 0.4, find the force (P) required moving the block B.
Sol. Given: Weight of block A (WA) = 5 KN; Weight of block B (WB) = 7 KN and coefficient of friction (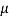 ) = 0.4.
) = 0.4.
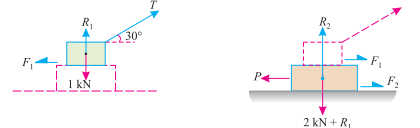
(i) Block A(ii) Block B
The forces acting on the two blocks A and B are shown in Fig. (A) and (B) respectively. First of all, consider the forms acting in the block A.
Resolving the force vertically
R1 + T sin 30° = 5
T sin30° = 5- R1……………………………… (i)
And resolving the force horizontally
Tcos30° = F1 = R1 =0.4 R1 ............................... (ii)
R1 =0.4 R1 ............................... (ii)
Dividing equation (i) by (ii)
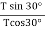 =
=  or tan30° =
or tan30° =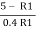
0.5774 = 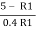 or 0.5774
or 0.5774  0.4R1 = 5- R1
0.4R1 = 5- R1
R1 = 4.06 KN
And F1 = 0.4  4.06 = 1.62 KN
4.06 = 1.62 KN
Now consider the block B. A little consideration will show that the downward force of the block (A) (equal to R1) will also act along with the weight of the block B.
Resolving the force vertically
R2 = 7 + R1 = 7 + 0.85 = 7.85 KN
F2 = 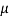 R2 = 0.4
R2 = 0.4  7.85 = 3.14 KN
7.85 = 3.14 KN
Now resolving the force horizontally
P = F1 + F2 = 1.62 + 3.14 = 4.76 KN
Q2. A body of weight 500 N is laying on a rough plane inclined at an angle of 25° with the horizontal. It is supported by an effort (P) parallel to the plane as shown in Fig.
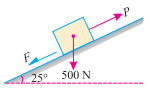
Determine the minimum and maximum values of P, for which the equilibrium can exist, if the angle of friction is 20°.
Sol. Given: Weight of the body (W) = 500 N; Angle at which plane is inclined (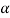 ) = 25° and angle of friction (
) = 25° and angle of friction ( ) = 20°.
) = 20°.
Minimum value of P
We know that for the minimum value of P, the body is at the point of sliding downwards. We also know that when the body is at the point of sliding downwards, then the force.
P1 =W 
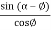 = 500
= 500 
 = 4.64 N
= 4.64 N
Maximum value of P
We know that for the maximum value of P, the body is at the point of sliding upwards. We also know that when the body is at the point of sliding upwards, then the force
P2 = W 
 = 500
= 500 
 = 376.2 N
= 376.2 N
Q3. An inclined plane as shown in Fig. Is used to unload slowly a body weighing 400 N from a truck 1.2 m high into the ground.

The coefficient of friction between the underside of the body and the plank is 0.3. State whether it is necessary to push the body down the plane or hold it back from sliding down. What minimum force is required parallel to the plane for this purpose?
Sol. Given: Weight of the body (W) = 400 N and coefficient of friction ( ) = 0.3. Whether it is necessary to push the body down the plane or hold it back from sliding down.
) = 0.3. Whether it is necessary to push the body down the plane or hold it back from sliding down.
We know that
Tan =
=  = 0.5 or
= 0.5 or 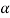 = 26.5°
= 26.5°
And normal reaction, R = W cos 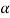 = 400 cos 26.5° N
= 400 cos 26.5° N
= 400 × 0.8949 = 357.9 N
∴ Force of friction
F = 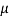 R = 0.3 × 357.9 = 107.3 N ...(i)
R = 0.3 × 357.9 = 107.3 N ...(i)
Now resolving the 400 N force along the plane
= 400 sin = 400 × sin 26.5° N
= 400 × sin 26.5° N
= 400 × 0.4462 = 178.5 N….(ii)
We know that as the force along the plane (which is responsible for sliding the body) is more than the force of friction, therefore the body will slide down. Or in other words, it is not necessary to push the body down the plane; rather it is necessary to hold it back from sliding down.
Minimum force required parallel to the plane
We know that the minimum force required parallel to the plane to hold the body back,
P = 178.5 – 107.3 = 71.2 N
Q4. An effort of 200 N is required just to move a certain body up an inclined plane of angle 15° the force acting parallel to the plane. If the angle of inclination of the plane is made 20° the effort required, again applied parallel to the plane, is found to be 230 N. Find the weight of the body and the coefficient of friction.
Sol. Given: First case: When effort (P1) = 200 N, then angle of inclination (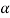 1) = 15° and second case: When effort (P2) = 230 N, then angle of inclination (
1) = 15° and second case: When effort (P2) = 230 N, then angle of inclination (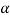 2) = 20°.
2) = 20°.
Let  = Coefficient of friction,
= Coefficient of friction,
W = Weight of the body,
R = Normal reaction, and
F = Force of friction.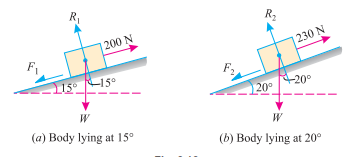
First of all, consider the body lying on a plane inclined at an angle of 15° with the horizontal and subjected to an effort of 200 N as shown in Fig. (a).
Resolving the forces at right angles to the plane,
R1 = W cos 15° ... (i)
And now resolving the forces along the plane,
200 = F1 + W sin 15° = 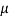 .R1 + W sin 15 °
.R1 + W sin 15 °
=  W cos 15° + W sin 15°
W cos 15° + W sin 15°
= W (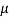 cos 15° + sin 15°)… (ii)
cos 15° + sin 15°)… (ii)
Now consider the body lying on a plane inclined at an angle of 20° with the horizontal and subjected to an effort of 230 N shown in Fig. (b).
Resolving the forces at right angles to the plane,
R2 = W cos 20°……… (ii)
And now resolving the forces along the plane,
230 = F22+ W sin 20° =  R2 + W sin 20°
R2 + W sin 20°
= W ( cos 20° + sin 20°) ……. (iv)
cos 20° + sin 20°) ……. (iv)
Coefficient of friction
Dividing equation (iv) by (ii)
 =
=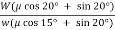
230 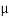 cos 15° + 230 sin 15° = 200
cos 15° + 230 sin 15° = 200 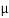 cos 20° + 200 sin 20°
cos 20° + 200 sin 20°
230 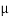 cos 15° – 200
cos 15° – 200  cos 20° = 200 sin 20° – 230 sin 15°
cos 20° = 200 sin 20° – 230 sin 15°
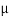 =0.259
=0.259
Weight of the body
Substituting the value of  in equation (ii)
in equation (ii)
200 = W (0.259 cos 15° + sin 15°)
= W (0.259 × 0.9659 + 0.2588) = 0.509 W
W = 392.9 N
Q5. A load of 1.5 KN, resting on an inclined rough plane, can be moved up the plane by a force of 2 KN applied horizontally or by a force 1.25 KN applied parallel to the plane. Find the inclination of the plane and the coefficient of friction.
Sol. Given: Load (W) = 1.5 KN; Horizontal effort (P1) = 2 KN and effort parallel to the inclined plane (P2) = 1.25 KN.
Inclination of the plane,
Let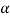 = Inclination of the plane, and
= Inclination of the plane, and
 = Angle of friction.
= Angle of friction.
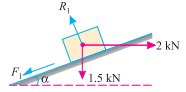

(a) Horizontal force(b) Force parallel to plane
First of all, consider the load of 1.5 KN subjected to a horizontal force of 2 KN as shown in figure. We know that when the force is applied horizontally, then the magnitude of the force, which can move the load up the plane.
P = W tan (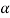 +
+ )
)
2 = 1.5 tan (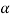 +
+ )
)
Tan ( +
+ ) =1.33 or (
) =1.33 or (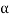 +
+ ) =53.1°
) =53.1°
Now consider the load of 1.5 KN subjected to a force of 1.25 KN along the plane as shown in figure. We Know that when the force is applied parallel to the plane, then the magnitude of the force, which can move the load up the plane,
P = W 

Or 1.25= 1.5 

Cos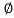 =0.96
=0.96
 = 16.3°
= 16.3°
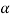 = 53.1° – 16.3° = 36.8°
= 53.1° – 16.3° = 36.8°
Coefficient of friction
We know that the coefficient of friction,
 = tan
= tan  = tan 16.3° = 0.292
= tan 16.3° = 0.292
Q6. Two blocks A and B, connected by a horizontal rod and frictionless hinges are supported on two rough planes as shown in figure.
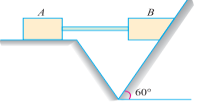
The coefficients of friction are 0.3 between block A and the horizontal surface, and 0.4 between block B and the inclined surface. If the block B weighs 100 N, what is the smallest weight of block A that will hold the system in equilibrium?
Sol. Given: Coefficient of friction between block A and horizontal surface (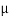 A) = 0.3; Coefficient of friction between block B and inclined surface (
A) = 0.3; Coefficient of friction between block B and inclined surface (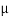 B) = 0.4 and weight of block B (WB) = 100 N.
B) = 0.4 and weight of block B (WB) = 100 N.
Let WA = Smallest weight of block A.
We know that force of friction of block A, which is acting horizontally on the block B
P = 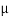 A WA = 0.3 × WA = 0.3 WA
A WA = 0.3 × WA = 0.3 WA
And angle of friction of block B
Tan  =
= 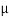 B = 0.4 or
B = 0.4 or  = 21.8°
= 21.8°
We also know that the smallest force, which will hold the system in equilibrium (or will prevent the block B from sliding downwards),
P = WB tan ( –
–  ) = 100 tan (60° – 21.8°)
) = 100 tan (60° – 21.8°)
Or 0.3 WA = 100 tan 38.2° = 100 × 0.7869 = 78.69
WA = 262.3 N
Q7. Find the force required to move a load of 300 N up a rough plane, the force being applied parallel to the plane. The inclination of the plane is such that when the same load is kept on a perfectly smooth plane inclined at the same angle, a force of 60 N applied at an inclination of 30° to the plane, keeps the same load in equilibrium.
Assume coefficient of friction between the rough plane and the load to be equal to 0.3
Sol. 1st case
Given: In this case load (P) = 60 N; Angle (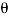 ) = 30° and force of friction F = 0 (because of smooth plane). Resolving the forces along the inclined plane,
) = 30° and force of friction F = 0 (because of smooth plane). Resolving the forces along the inclined plane,
60 cos 30° = 300 sin 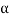
Sin 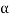 = 0.1732 or
= 0.1732 or 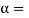 10°
10°
2nd case
Given: In this case, coefficient of friction ( ) = 0.3 = tan
) = 0.3 = tan  or
or  = 16.7°
= 16.7°
Let P = Force required to move the load up the plane,
R = Normal reaction, and
F = Force of friction equal to 0.3 R.
Resolving the forces along the plane,
P = F + 300 sin 10° = 0.3 R + (300 × 0.1732) = 0.3 R + 51.96 N …. (i)
And now resolving the forces at right angles to the plane,
R = 300 cos 10° = 300 × 0.9849 = 295.5 N…. (ii)
Substituting the value of R in equation (i),
P = (0.3 × 295.5) + 51.96 = 140.7 N
Q8. The upper half of an inclined having inclination 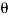 with the horizontal is smooth, while the lower half in rough as shown in figure.
with the horizontal is smooth, while the lower half in rough as shown in figure.
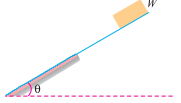
If a body of weight W slides down from rest at the top, again comes to rest at the bottom of the plane, and then determine the value of coefficient of friction for the lower half of the plane.
Sol. Given: Angle of inclination =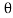 and weight of the body = W
and weight of the body = W
Let 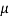 = Coefficient of friction for the lower half of the inclined alone
= Coefficient of friction for the lower half of the inclined alone
We know that acceleration on the smooth surface of the plane
= g sin 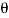 ……………. (i)
……………. (i)
And retardation on the rough surface of the plane
= – g (sin 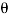 –
– 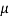 cos
cos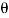 )
)
= g (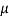 cos
cos  – sin
– sin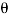 ) …………….. (ii)
) …………….. (ii)
Since body starts from rest at the top comes to rest at the bottom of therefore acceleration on the smooth surface is equal to retardation on the rough surface.
g sin 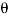 = g (
= g ( cos
cos  – sin
– sin 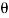 ) or sin
) or sin 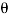 =
= 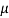 cos
cos  – sin
– sin 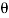
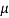 Cos
Cos  = 2 sin
= 2 sin 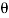 or
or 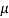 = 2 tan
= 2 tan 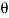
Q9. Two identical blocks of weight W are supported by a rod inclined at 45° with the horizontal as shown in figure.
If both the blocks are in limiting equilibrium, find the coefficient of friction (μ), assuming it to be the same at floor as well as at wall.
Sol. Given: Weight of blocks A and B = W and inclination of rod with the horizontal ( ) = 45°.
) = 45°.
Let = Coefficient of friction, and
= Coefficient of friction, and
l = Length of the rod.
The forces acting on both the blocks are shown in Fig.
Resolving the forces vertically.
FW + RF = 2W
 RW + RF = 2W…………… (i)
RW + RF = 2W…………… (i)
And now resolving the forces horizontally
RW = FF = 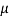 RF…………… (ii)
RF…………… (ii)
Now substituting this value of RW in equation (i)
 (
(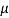 RF) + RF = 2W
RF) + RF = 2W
 RF + RF = 2W
RF + RF = 2W
RF = 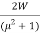 …………… (iii)
…………… (iii)
And now substituting this value of RF in equation (ii),
RW = 
Taking moments of the forces about the block A and equating the same,
RW × l cos 45° + FW × l cos 45° = W × l cos 45°
RW + FW = W
RW (1 + ) = W
) = W
Substituting the value of RW from equation (iv),
 (1 +
(1 +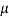 ) = W
) = W
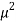 + 2
+ 2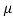 – 1 = 0
– 1 = 0
Solving it as quadratic equation for 
 = 0.414
= 0.414
Q10. A uniform ladder of weight of 300 N rests against a smooth vertical wall a rough horizontal floor making at angle 60 with the horizontal. Find the force of friction at floor.
Sol. Draw free body diagram of ladder AB and apply condition of equilibrium.
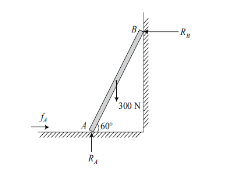
As the wall is smooth, 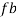 = 0
= 0
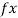 = 0
= 0
FA = RA
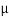 RA = RB
RA = RB
 = 0
= 0
RA = W = 300N
FA =  RA = 300
RA = 300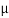
Assume µ = 0.3 between ladder and floor
The force of friction,
FA = 90 N