UNIT 1
Q.1 List the conditions a wave function must satisfy in order to solve the Schrödinger equation.
Answer:
1. The wave function ψ must be continuous. All its partial derivatives must also be continuous.
This makes the wave function “smooth”.
2. The wave function ψ must be quadratically integrable. This means that the integral
 must exist.
must exist.
3. Since

is the probability density, it must be single valued?
4. The wave functions must form an orthonormal set. This means that • the wave functions must be normalized.
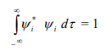
• the wave functions must be orthogonal.
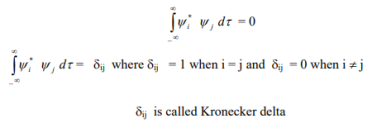
5. The wave function must be finite everywhere.
6. The wave function must satisfy the boundary conditions of the quantum mechanical system it represents.
Q.2 State and Derive the time independent Schrodinger wave equation?
Answer:
According to de-Broglie theory, for a particle of mass ‘m’, moving with a velocity ‘v’, the wavelength associated with it is
λ=h/p
The wave equation for a de-Broglie wave can be written in complex notation as:
 …………1
…………1
Where, A is the amplitude, ω is angular frequency and k is the wave vector.
Differentiate equation (1) with respect to ‘t’ twice, we get

We have differential equation for the traveling wave as,
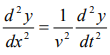 ……….3
……….3
Where, y is displacement and ‘v’ is velocity of wave.
By analogy, we can write the wave equation for de-Broglie wave associated with the motion of a free particle as,
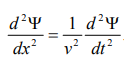 ………4
………4
This represents the de-Broglie wave propagating along x-direction with a velocity ‘v’ and ‘Ψ’ is the displacement.
From equation (2) and (4),
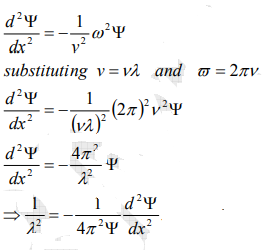 …………..5
…………..5
The kinetic energy of a moving particle of mass ‘m’ and velocity ‘v’ is given by
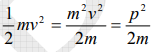
But we have from equation (1), p = (h/λ)
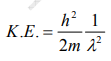
Substitute for (1/ λ)2 from equation (5),
 …………….6
…………….6
Let there be a field where the particle is present. Depending on its position in the field, the particle will possess certain potential energy. Then we can write:
Total energy = Kinetic energy + Potential energy
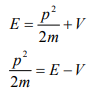
From equation (6), we can write

This is the time independent Schrödinger’s wave equation in one-dimension.
Q.3 An electron is bound in one-dimensional infinite well of width 1 × 10–10 m. Find the energy values in the ground state and first two excited states?
Answer:
Potential well of width (L) = 1 × 10–10 m
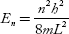
For ground state n = 1,
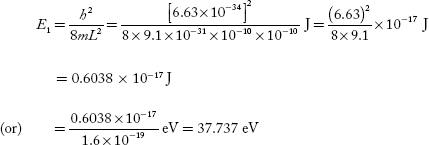
E2 = 4E1 = 2.415 × 10−17 J
= 150.95 eV
E3 = 9E1 = 5.434 × 10−17 J
= 339.639 eV.
Q.4 What is the de Broglie wavelength of an electron that is accelerated from rest through a potential difference of 10V?
Answer:
Since an electron is a particle with mass, it can be described by the de Broglie relation:
λ=hm/v
Where:
- h=6.626×10−34J⋅s is Planck's constant.
- Me=9.109×10-31kg is the rest mass of an electron.
- v is its speed.
It is also moving with a certain speed; it will have a kinetic energy of:
K=1/2mv2=p2/2m
Where:
- p=mv is the linear momentum of the particle.
- m is the mass of the particle.
- v is the speed of the particle.
And so, we can get the forward momentum in terms of the kinetic energy:
p=√2mK=mv
Lastly, note that in 1 eV, there is 1.602×10-19 J, i.e. one needs 1 eV to push one electron’s worth of charge through a potential difference of 1 V in an electric field.
Therefore, the de Broglie wavelength of the electron is:
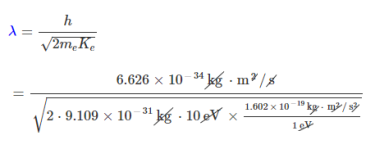
=3.88×10-10m
= 0.388 nm
Q.5 Prove that electron does not exist in nucleus?
Answer:
The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.
Non-existence of electrons in the nucleus:
But to prove it, let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14 m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by:
∆x= 10-14 m
According to uncertainty principle,
∆x∆px =h/2∏
Thus ∆px=h/2∏∆x
Or ∆px =6.62 x10-34/2 x 3.14 x 10-14
∆px=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron ,then the momentum of electron should be at least of this order, that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E= √ m20 c4 + p2c2
E = √(9.1*10-31)2 (3*108)4 + (1.05*10-20)2(3*108)2
= √(6707.61*10-30) +(9.92*10-24)
=(0.006707*10-24) +(9.92*10-24)
= √9.9267*10-24
E= 3.15*10-12 J
Or E=3.15*10-12/1.6*10-19 eV
E= 19.6* 106 eV
Or E= 19.6 MeV
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV. However, it is observed that beta-particles (electrons) ejected from the nucleus during b –decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV. Second reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
Q.6 Write down the Schrodinger wave equation for a particle in a
I-Dimensional Deep potential well?
Answer:
The potential function is expressed as
 for
for  ……..(1)
……..(1) for
for  ……..(2)
……..(2)
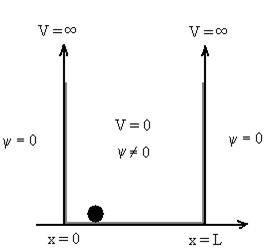
Figure: Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e.  ). Inside the well, the Schrödinger wave equation is written as
). Inside the well, the Schrödinger wave equation is written as
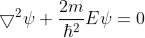 ……..(3)
……..(3)
Substituting 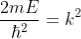 ……..(4), and writing the SWE for 1-D
……..(4), and writing the SWE for 1-D
We get 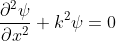 ……. (5)
……. (5)
The general equation of above equation may be expressed as
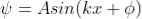 ……. (6)
……. (6)
Where A and 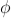 are constants to be determined by boundary conditions
are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation (6)
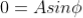
As  then
then 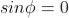 or
or  ……... (7)
……... (7)
Condition II: Further ψ = 0 at x = L, and  ,therefore from equation (6)
,therefore from equation (6)
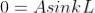
As 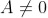 then
then or
or 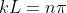
 n = 1,2,3, 4, ……. (8)
n = 1,2,3, 4, ……. (8)
Substituting the value of k from (8) to (4)
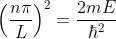
This gives 
 n = 1,2,3,4,…. ……..(9)
n = 1,2,3,4,…. ……..(9)
From equation (9) En is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.
Using (7) and (8) equation (6) becomes, the corresponding wave functions will be
 ……..(10)
……..(10)
The probability density 
 ……..(11)
……..(11)
The probability density is zero at x = 0 and x = L. Since the particle is always within the well 
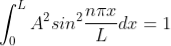
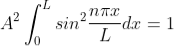
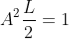

Substituting A in equation (9), we get
 ; n = 1,2,3,4,…. … (12)
; n = 1,2,3,4,…. … (12)
The above equation (12) is normalized wave function (Eigen function) belonging to energy value En
Q.7 Describe quantum computing?
Answer:
Quantum computing is essentially harnessing and exploiting the amazing laws of quantum mechanics to process information. A traditional computer uses long strings of “bits,” which encode either a zero or a one.
A quantum computer, on the other hand, uses quantum bits, or qubits. What's the difference? Well a qubit is a quantum system that encodes the zero and the one into two distinguishable quantum states. But because qubits behave quantumly
Quantum computer can process a vast number of calculations simultaneously. Think of it this way: whereas a classical computer works with ones and zeros, a quantum computer will have the advantage of using ones, zeros and “superpositions” of ones and zeros. Certain difficult tasks that have long been thought impossible (or “intractable”) for classical computers will be achieved quickly and efficiently by a quantum computer.
When you enter the world of atomic and subatomic particles, things begin to behave in unexpected ways. In fact, these particles can exist in more than one state at a time. It’s this ability that quantum computers take advantage of.
Q.8 Define phase velocity and group velocity?
Answer:
Phase Velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space.
This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity.
The phase velocity is given in terms of the wavelength λ (lambda) and period T as
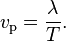
In terms of the wave’s angular frequency ω, which specifies the number of oscillations per unit of time, and wavenumber k, which specifies the number of oscillations per unit of space, by
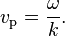
Group Velocity
The group velocity of a wave is the velocity with which the overall shape of the wave’s amplitudes — known as the modulation or envelope of the wave — propagates through space.
The group velocity defined by the equation-
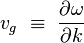
Where ω is the wave’s angular frequency (usually expressed in radians per second), and k is the angular wavenumber (usually expressed in radians per meter). The function ω(k), which gives ω as a function of k, is known as the dispersion relation.
Q.9 Calculate the minimum energy of free electron trapped in a one-dimensional box of width 0.2 nm. (Given, h = 6.63 –10–34 J-S and electron mass × 9.1 × 10 –31 kg)
Answer:
One-dimensional box of width, L = 0.2 nm = 2 × 10–10 m
Minimum energy of the electron, E1 =?
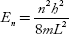
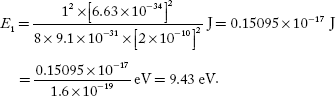
Q.10 Discuss Heisenberg’s uncertainty principal?
Answer:
According to this –
It is impossible to determine simultaneously both the position and momentum of a quantum mechanical particle moving inside the wave packet with equal accuracy. In any simultaneous determination of the position and momentum of a particle, the product of the corresponding uncertainties inherently present in the measurement is equal to, greater than (h/4π).
The maximum uncertainty involved in measuring the position of the particle within the wave packet is Δx. Since position cannot be measured accurately, there will be an uncertainty in measuring momentum also. According to Heisenberg’s uncertainty principle, the product of uncertainty involved in the measurement of these two quantities is given by the relation,
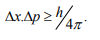
Where ∆x = uncertainty in position.
∆p = uncertainty in momentum.
It can be applied to any conjugate physical quantities such as energy and time, angular position and angular momentum etc.
Other forms of Uncertainties are:
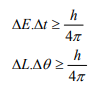
Where, ΔE, Δt are the uncertainties in the measurement of energy and time, and ΔL, Δθ are the uncertainties in the measurement of angular momentum and angular position.