Question Bank
Unit 4
Q.1 Newton’s rings are observed in the reflected light of wave length 5900 Å. The diameter of 10th dark ring is 0.5 cm. Find the radius of curvature of the lens used.
Answer:
The given data are
Wave length of light (λ) = 5900 Å= 5900 × 10–10 m
Diameter of 10th Newton’s dark ring (D10) = 0.5 cm = 0.5 × 10–2 m
Radius of curvature of lens (R) =?
Formula is D2n = 4nλR
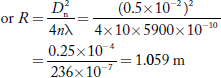
Q 2 Calculate the thickness of air film at the 10th dark ring in a Newton’s rings system, viewed normally by a reflected light of wave length 500 nm. The diameter of the 10th dark ring is 2 mm.
Answer:
Given data are
Wave length of light (λ) = 500 nm = 500 × 10–9 m
Number of the dark ring viewed (n) = 10
Diameter of 10th dark ring (D10) = 2 mm = 2 × 10–3 m
Radius of 10th dark ring 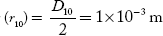
Thickness of air film (t) =?
Condition for dark ring is
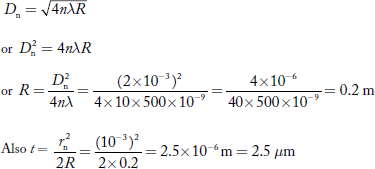
Q .3 Two coherent sources whose intensity ratio is 36:1 produce interference fringes. Deduce the ratio of maximum intensity to minimum intensity.
Answer:
Intensities ratio of coherent sources = a21 : a22 = 36: 1
∴ a1 : a2 = 6: 1
Minimum intensity of the interference fringe = (a1 – a2)2
= (6 – 1)2 = 25
Maximum intensity of the interference fringe = (a1 + a2)2
= (6 + 1)2 = 49
The ratio of maximum intensity to minimum intensity = 49 : 25 ≈ 2 : 1
Q. 4 Explain interference in wedge shaped film?
Answer:
Interference in Wedge Shaped Film (Reflected Rays)
The wedge-shaped film has a thin film of varying thickness, having thickness zero at one end and increases at the other. The angle of wedge is 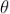 .
.
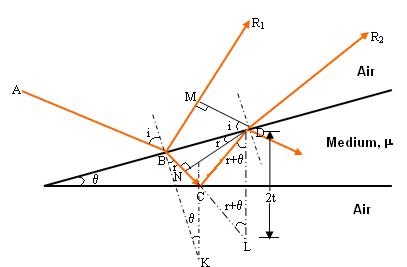
The optical path difference between the two reflected rays R1 and R2 will be
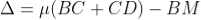
From the geometry
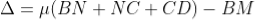
As in ΔBMD;
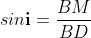
And in ΔBND
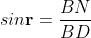
According Snell’s Law,
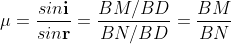
Or 
Thus 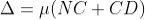
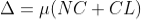
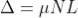
As in ΔNDL
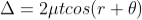
Correction on account of phase change at reflection: when a beam is reflected from a denser medium (ray R1 at B), a path change of  /2 occur for the ray.
/2 occur for the ray.
There-fore the true path difference is
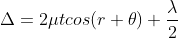
Condition of Maxima (Bright Fringe)
Maxima occur when path difference,
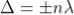
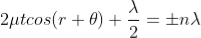
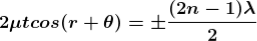
Condition for Minima (Dark Fringe)
Minima occur when path difference
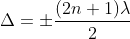
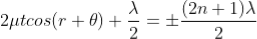

Q. 5 How test that surface is flat or not by interference?
Answer:
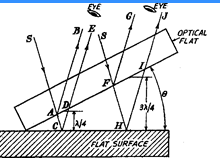
If an optical flat is placed upon another flat reflecting surface (without pressure) it willnot form an intimate contact, but will lie at some angle 0 making an inclined plane. If theoptical flat be now illuminated by monochromatic source of light, the eye if placed in properposition, will observe a number of bands. These are produced by the interference of the light
rays reflected from the lower surface of the top flat and the top surface of the lower flat throughthe very thin layer of air between the flats. the angles 6 between the two flats is shown exaggerated too much. S is the source of monochromatic light. At point A, the wave of
incident beam from S is partially reflected along AB and is partially transmitted across the
air gap along AC. At C, again the ray is reflected along CD and passes out towards the eye
along CDE. Thus, the two reflected components, reflected at A and C are collected and
recombined by the eye, having travelled paths whose lengths differ by an amount ACD.
If the path lengths of the two components differ by an odd number of half wavelengths,
then condition for complete interference is achieved. If the surface is perfectly flat, thencondition of complete interference is satisfied in a straight line across the surface as the surfaceat right-angles to the plane of the paper is parallel to the optical flat. Therefore, a straightdark line will be seen passing through point C. Consider another ray incident along path SFH. Again, this ray is also spilatted into two components. It is obvious that the path difference of the two component rays will keep on increasing along the surface due to angle 9.
Thus, if the path difference FHI be 3X12 or the next odd number of half wavelengths, then interference will occurand a similar fringe will be seen. Next when path difference is 5K/2, again there will be another dark fringe. At the intermediate point between the points C and H, the path difference will be an even number of half wavelengths and the two components will be in phase producing a light band.
Thus, in case of a perfectly flat surface, we will have pattern of alternate light and darkstraight lines on the surface. Any deviation from this pattern will be a
measure of the error in the flatness of the surface being inspected.
Q 6 Determine thickness of thin foil?
Answer:
DIAMETER OF A THIN WIRE:
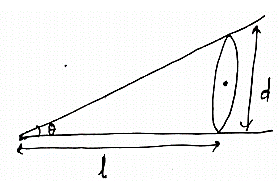
Take two optically flat glass plates and held them together at one end so that a wedge-shaped air film is formed with a very small wedge angle ѳ. At other end put the wire or foil whose diameter is to be determined. From the figure, tan ѳ = d/l……………………. (1)
Also, tan ѳ =λ/2μꞵ……………. (2)
From 1 &2
d/l = λ / 2μꞵi.e. d = lλ / 2ꞵ
For an air film μ =1, which is distance between two dark or bright/dark bands can be measured experimentally. Therefore, diameter can be determined.
Q. 7 In a Newton’s ring experiment, the diameter of the 5th ring is 0.30 cm and diameter of the 15th ring is 0.62cm. Find the diameter of the 25th ring
Answer:
Diameter of Newton’s 5th ring = 0.30 cm
Diameter of Newton’s 15th ring = 0.62 cm
And Diameter of Newton’s 25th ring = ?
From Newton’s rings experiment we know
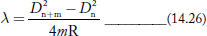
Or D2n+m − D2n = 4λmR
For 5th and 15th rings
D215 − D25 = 4λ× 10 × R _______ (1) (m = 10)
For 15th and 25th rings
D225 − D215 = 4λ× 10 × R _______ (2) (m = 10)
Equation (2) = Equation (1)
D225 − D215 = D215 − D25
Or D225 = 2D215 – D25
Substituting the values,
D225 = 2 × 0.62 × 0.62 – 0.3 × 0.3 =0.6788 cm2
∴ D25 = 0.8239 cm
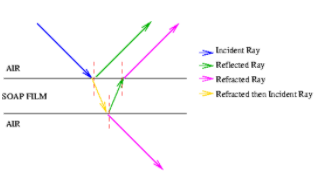
Q. 9 A soap film of refractive index 1.33 and thickness 5000 Å is exposed to white light. What wave lengths in the visible region are reflected?
Answer:
The given datais
Refractive index of soap (μ) = 1.33
Thickness of soap film (t) = 5000 Å = 5000 × 10–10 m
What wave lengths in the visible light are reflected?
The incident light reflected on both surfaces of film combine to produce interference. So, the condition for constructive interference is used for reflection.
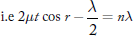
For maximum reflection cos r = 1

Q .10 How colours are origin in thin film?
Answer:
Everyone is familiar with the brilliant colours exhibited by a thin oil film spread on the surface of water and also by a soap bubble. These colours are due to interference between light waves reflected from the top and the bottom surfaces of thin films. When white light is incident on a thin film, the film appears coloured and the colour depends upon the thickness of the film and also the angle of incidence of the light.