Unit-2

Matrices and determinants

Q1) check whether the following matrix A is symmetric or not?

A = 

A1)

 As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.

So that, first we will find its transpose,

Transpose of matrix A ,

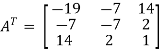
Here,

                                   A =

The matrix A is symmetric.

Q2) If A = 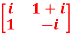  then show that

(i) 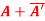is hermitian matrix.

(ii)   is  skew-hermitian matrix.

A2)

Given   A =

Then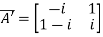 

Let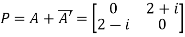

Also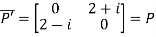  

Hence P is a Hermitian matrix.

Let

Also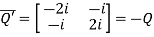

Hence Q is a   skew-hermitian matrix.

Q3) check whether the following matrix A is symmetric or not?

                                            A =

A3)

This is not a skew symmetric matrix, because the transpose of matrix A is not equals to  -A.

-A = A’

Q4) Add .

A4)

A + B =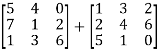

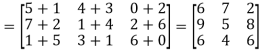
Q5)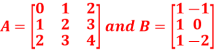

A5)

Then

Q6) Find out the determinant of the following matrix A.

A6)

By the rule of determinants-

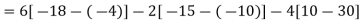
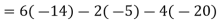
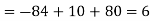
Q7) Expand the determinant:

A7)

As we know

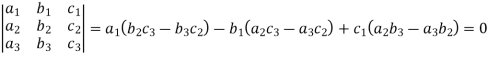
Then,                         

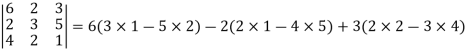
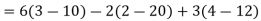
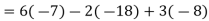
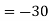
Q8) Find the minors and cofactors of the first row of the determinant.

A8)

(1)  The minor of element 2 will be,

Delete the corresponding row and column of element 2,

We get,

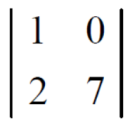
Which is equivalent to, 1 × 7 - 0 × 2 = 7 – 0 = 7

Similarly the minor of element 3 will be,  

4× 7 - 0× 6 = 28 – 0 = 28

Minor of element 5,  

4 × 2 - 1× 6 = 8 – 6 = 2

The cofactors of 2, 3 and 5 will be,

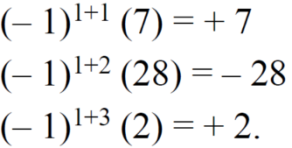
Q9) Solve-

A9)

Given

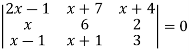
Apply-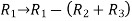

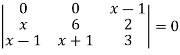
We get-

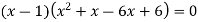
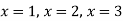
Q10) Show that the points given below are collinear-

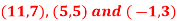
A10)

First we need to find the area of these points and if the area is zero then we can say that these are collinear points-

So that-

We know that area enclosed by three points-

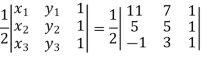
Apply-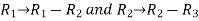

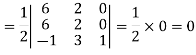
So that these points are collinear.

Q11) Solve the following equations by using Cramer’s rule-

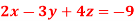
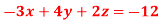
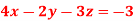
A11)

Here we have-

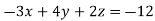
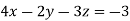
And here-

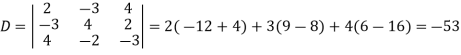
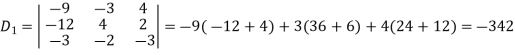
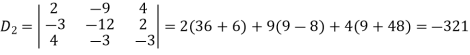
Now by using cramer’s rule-

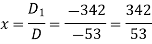
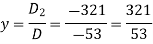
Q12) Find the inverse of matrix ‘A’ if-

A12)

Here we have-

Then

And the matrix formed by its co-factors of |A| is-

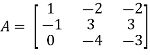
Then

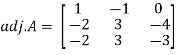
Therefore-

We know that-

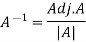
Q13) Find the inverse of matrix ‘A’ by using elementary transformation-

A =

A13)

Write the matrix ‘A’ as-  

A = IA

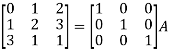
Apply , we get

Apply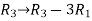

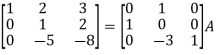
Apply

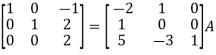
Apply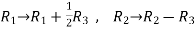

Apply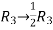

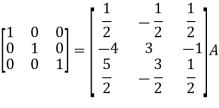
So that,

  =

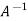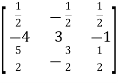
Question-14: The following inter-industry transactions table was constructed for an economy of the year 2019-

Now construct the technology co-efficient matrix showing direct requirement.

A14)

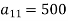
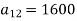
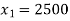
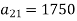
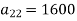
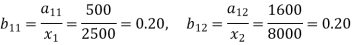
The technology matrix is-

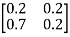
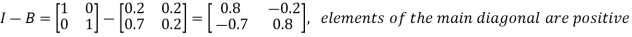
Now-

Since the diagonal elements are positive and is positive.

Here Hawkins-Simon conditions are satisfied.

Hence the system has a solution.