Unit-3
Derivatives and applications of derivatives
Q1) Evaluate the 
A1)
We can simply find the solution as follows,

Q2) evaluate 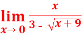
A2)
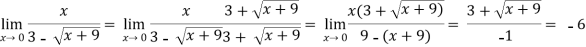
Q3) Find dy/dx of the following functions-
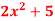

A3)
Let y = 
Then-
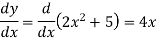
and
Let y = 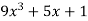
Then-
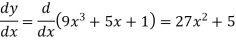
Q4) Differentiate 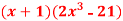 with respect to x.
with respect to x.
A4)
Let 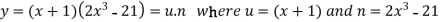
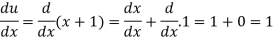
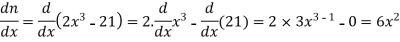
Now
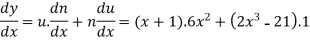
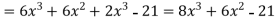
Q5) if y = 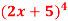 then find dy/dx.
then find dy/dx.
A5)
Suppose z = 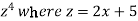
Now-
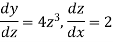
So that-
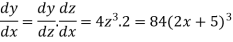
Q6) If y = log log log 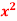 then find dy/dx.
then find dy/dx.
A6)
Suppose y = log u where u = log v and v = log 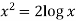
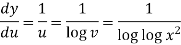
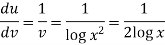
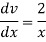
So that-
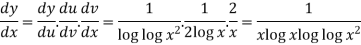
Q7) if y = 
A7)
Let y = log u where u = 
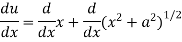
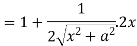
Now
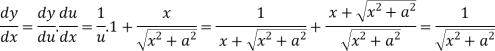
Q8) Calculate  and
and 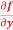 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
A8)
To calculate 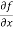 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
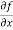 =
= 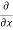 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 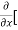 3x³] -
3x³] -  5y²] +
5y²] + 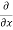 [2xy] -
[2xy] -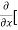 8x] +
8x] +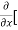 4y] -
4y] - 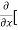 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
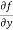 =
= 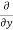 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 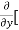 3x³] -
3x³] - 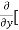 5y²] +
5y²] + 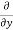 [2xy] -
[2xy] -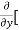 8x] +
8x] +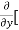 4y] -
4y] -  20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Q9) if 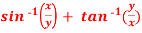 , then show that-
, then show that- 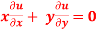
A9)
Here we have,
u =  …………………..(1)
…………………..(1)
now partially differentiate eq.(1) w.r to x and y , we get
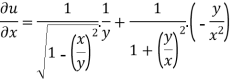
= 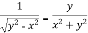
Or
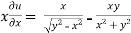 ………………..(2)
………………..(2)
And now,
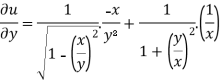
= 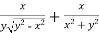
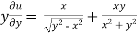 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
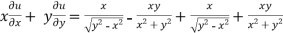 = 0
= 0
Hence proved.
Q10) if y = log x/ x a then find 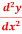
A10)
First we will find the first derivative-

Now
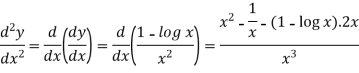

Q11) Examine for maximum and minimum for the function f(x) = 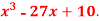
A11)
Here the first derivative is-
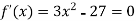

So that, we get-
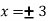
Now we will get to know that the function is maximum or minimum at these values of x.
For x = 3
Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).
Then-
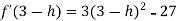 which is negative for h is very small
which is negative for h is very small
 which is positive.
which is positive.
Thus f’(x) changes sign from negative to positive as it passes through x = 3.
So that f(x) is minimum at x = 3 and the minimum value is-
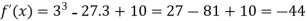
And f(x) is maximum at x = -3.
Q12) Find out the value of x for which the function f(x) = 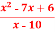 is minimum of maximum.
is minimum of maximum.
A12)
Let y = f(x) = 
Then the first derivative will be-

Putting 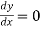 , we get-
, we get-

By using middle term splitting-
We get-
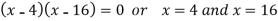
Now we will find the second derivative-
We get-
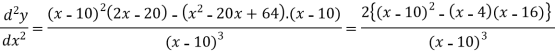
Here
At x = 4, 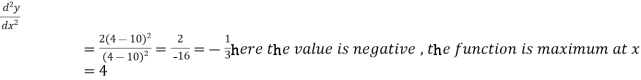
At x = 16, 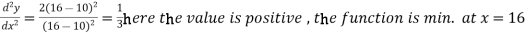
Q13) The total cost function of the firm is given by-

Where x is the output.
Find out-
A13)
Here we have-
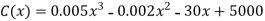
Now
FC = 5000
2. Average cost = TC/x = 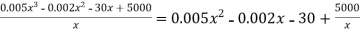
3. MC = d TC / dx 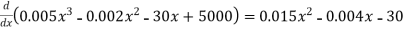
4. Marginal average cost = d AC / dx = 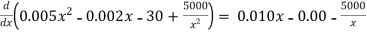
Q14) A manufacturer can sell x items per month at a price p = 300 – 2x rupees. Produced items cost the manufacturer y rupees y = 2x + 1000. How much profit will yield maximum profits
A14)
Profit (P) = Sale – total cost = x. p – y
= x (300 – 2x) – (2x + 1000) = 298x – 2 – 1000
– 1000
For maximum profit-
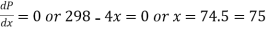
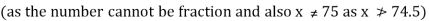
Again the second derivative is-

Hence the profit will be maximum for 74 items.
Q15) A belt manufacturer produces high grade and low grade shoes in x units (hundred pairs) and y units (hundred pair) per day respectively.
Assume that the equipment is capable of producing the belts in the following relationship-
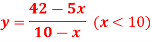
If the high grade belt are sold at a price twice the low grade belts.
Determine the pairs of both the belts he should produce to maximize his total revenue.
A15)
let the price of low grade belt be Rs. p per pair, then the price of high grade belts will be rs. 2 p per pair.
The total revenue will be-

Or
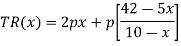
For maximizing TR(x), take its first derivative w.r.t. x, put it equal to zero and solve for x,

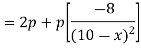
Now put it equals to zero and solving for x,
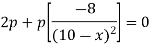
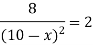
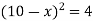
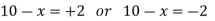
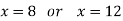
So that,
x = 8 [ x< 10, and x = 12 is not possible]
Now at x = 8,
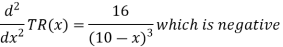
RT(x) is maximum at x = 8
Put this value in the function-
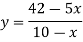
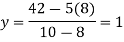
So that we can conclude that the total revenue is maximum when the manufacturer produces 800 pairs of high grade and 100 pairs of low grade.
Q16) The Namkeen industry decides to reduce the price of its product, from Rs.100 to Rs. 75. The company expects that the sales of Namkeen will increase from 10,000 units a month to 20,000 units a month. Calculate and comment on the price elasticity of demand.
A16)
First, we need to calculate the percentage change in quantity demanded and percentage change in price. So,
% Change in Price = (Rs. 75-100)/(Rs.100) = -25%
% Change in Demand = (20,000-10,000)/(10,000) = 100%
Therefore, the Price Elasticity of Demand = 100%/-25% = -4.
This means the demand is relatively elastic