Unit - 1
Hyperbolic functions
Q1) What do you understand by the higher order derivatives?
A1)
It is the process of differentiating the given function simultaneously many times and the result obtained are called successive derivative.
Let 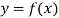 be a differentiable function.
be a differentiable function.
First derivative is denoted by 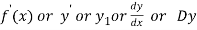
Second derivative is 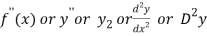
Third derivative is 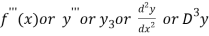
Similarly the nth derivative is 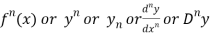
Q2) What is the n’th derivative of 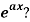
A2)
Suppose y = 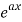 ,
,
Differentiate with respect to x successively, we get
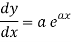
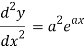

.
.
.
For n times differentiation, we get-
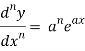
So we can say that its n’th derivative will be
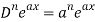
Q3) Find the n’th derivative of log(ax + b).
A3)
Suppose y = log (ax + b)
Differentiate with respect to x successively, we get
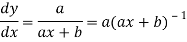
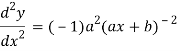
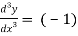 (-2)
(-2) 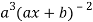
For n times differentiation, we get-
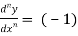 (-2)…………….(-n + 1)
(-2)…………….(-n + 1) 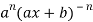
= 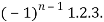 …………….(n - 1)
…………….(n - 1) 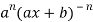
= 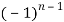 (n - 1)
(n - 1)
So we can say that its n’th derivative will be

Q4) If y = l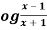 , then show that-
, then show that-
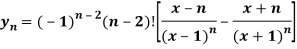
A4)
We have,
y = 
Differentiate y with respect to x, we get
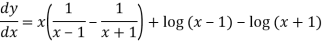
= 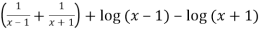
Again diff. (n – 1) times w.r .t x , we get-
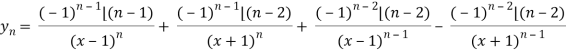
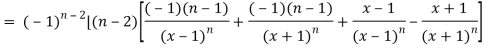
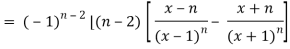
Q5) Find the  derivative of
derivative of 
A5)
Here we have-
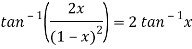
Suppose, y = 
First derivative-

Here ,
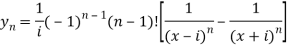
Let x = 
So that

Which is the n’th derivative of the given function.
Q6) Find cos x cos 2x cos 3x.
A6)

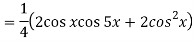
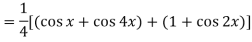
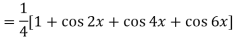
So that-
n’th derivative-
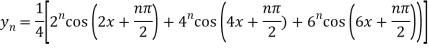
Q7) Find the 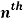 derivative of the following function-
derivative of the following function-
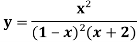
A7)
Partial fraction of the function y after splitting-
Suppose x – 1 = z, then
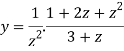
= 
= 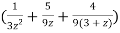
= 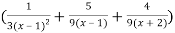
Here we can find its n’th derivative-

Q8) If y 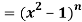 , then prove that-
, then prove that-
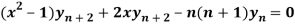
A8)
Here it is given that-
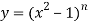
On differentiating-

Or
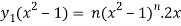
= ny.2x
Differentiate again with respect to x, we get-
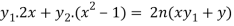
Or
 …………………. (1)
…………………. (1)
Differentiate each term of (1) by using Leibnitz’s theorem, we get-
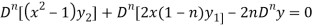
[ (x2 – 1) yn+2 + nyn+1 (2x)+ n(n-1)/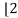 yn(2)] + 2 (1 – n)[ xyn+1 + nyn] – 2nyn = 0
yn(2)] + 2 (1 – n)[ xyn+1 + nyn] – 2nyn = 0
Therefore we get-
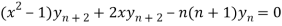
Hence proved.
Q9) If y = 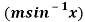 , then prove that-
, then prove that-
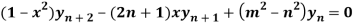
A9)
It is given that- y = 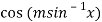
First derivative –
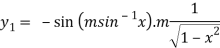
It becomes-
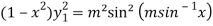
= 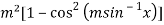
= 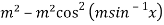
= 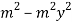
Becomes-
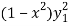 +
+  -
- 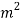 = 0
= 0
Om differentiating again we get-
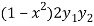 +
+ 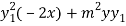 = 0
= 0
Or
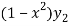 +
+ 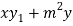 = 0
= 0
Differentiate n times by using Leibnitz’s theorem, we get-
yn+2(1 – x2) + nC1 yn+1 (-2x) + nC2 yn(-2) – [yn+1. x+ nC1. yn. 1] + m2yn = 0
(1 – x2)yn+2 – 2nx yn+1 – n(n – 1)yn – xyn+1 – nyn + m2yn = 0
So that
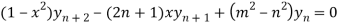
Hence proved.
Q10) If 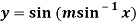 , then show that
, then show that
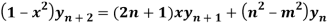
A10)
Also, find 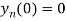
Here 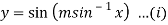
Differentiating with respect to x, we get
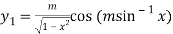 …(ii)
…(ii)
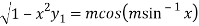
Squaring both side we get
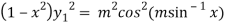
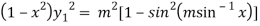
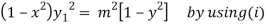
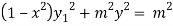 …(iii)
…(iii)
Again differentiating with respect to x ,we get
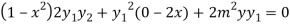

Using Leibnitz’s theorem we get

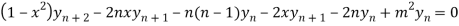
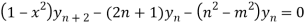 …(iv)
…(iv)
Putting x=0 in equation (i),(ii) and (iii) we get

Putting n=1,2,3,4….
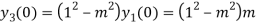
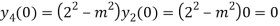
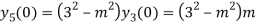
………………
Hence 
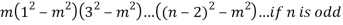
Q11) Determine the vertical asymptote of the function-
A11)
Here we have-
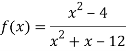
We can write the given function as-
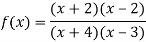
We can notice here as x gets closer to 3 from the left, then the value of the function gets smaller, approaching -∞ and x gets closer 3 from the right, then the value of the function gets larger and approaches +∞.
So that x = 3 is a vertical asymptote same as x = -4 is another vertical asymptote.
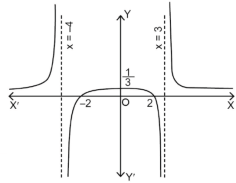
Q12) Find the horizontal asymptote of the function-
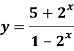
A12)
Find the limits-
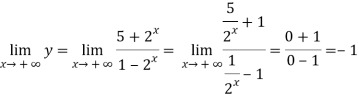
And
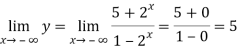
Hence the horizontal asymptotes are y = -1 and y = 5.
Figure will be as follows of the asymptotes of the given function-
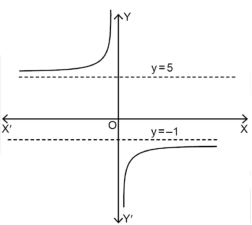
Q13) Find the slant asymptotes of 
A13)
We have,
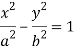
Which can be written as-
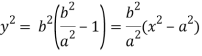
The value of ‘m’ will be-
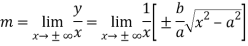
= 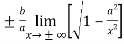 =
= 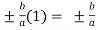
Now we can find ‘c’ as –
c = 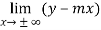 =
= 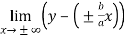 =
= 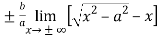
= 0
Hence the slant asymptotes are 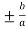
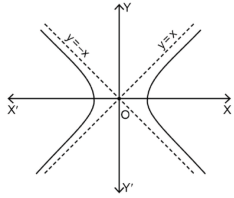
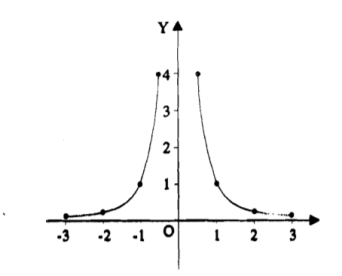
Q14) Trace the curve y = 1/x².
A14)
As we can see y- coordinates of the curve can not be negative. So the curve must be above x-axis. The curve is also symmetric about y-axis so we can draw the graph only in single side.
Here, we will find the first and second derivatives-
So, dy/dx= -2/x³ and d²y/dx² = 6/ x⁴ , here dy/dx <0 for all x>0 so we can say that the function is non- increasing so the graph falls as we increase x.
Also second derivative is also non zero so there are no point of inflection.
Here the curve is x²y=1 (rewritten), here both the axes are asymptotes of the curve.
Here is the figure of the curve-:
Q15) Trace the curve r = a(1+ cos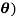 .
.
A15)
Here we can see clearly cos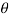 = cos(-
= cos(-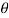 ), hence the curve is symmetric about initial line.
), hence the curve is symmetric about initial line.
Since -1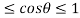 , the curve lies inside the circle r = 2a
, the curve lies inside the circle r = 2a
 = -asin
= -asin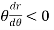 , when 0
, when 0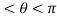 , thus r decreases as
, thus r decreases as 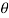 increases in the interval 0 to
increases in the interval 0 to 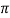
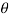 |
0 |
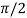 |
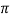 |
r |
2a |
A |
0 |
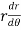 = - cot (
= - cot ( ) = tan(
) = tan(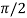 +
+  ), this shows the angle between r and
), this shows the angle between r and 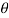 and the tangent is 0 or
and the tangent is 0 or 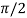 according to
according to 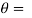 0 or
0 or  . Hence the line joining a point on the curve to the origin is orthogonal to the tangent when
. Hence the line joining a point on the curve to the origin is orthogonal to the tangent when = 0 and coincides with
= 0 and coincides with 
From the above results, we can easily draw the graph above the initial line
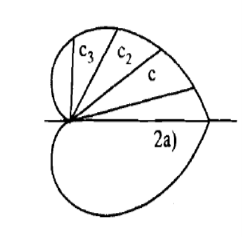
Q16) Trace the curve 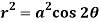 .
.
A16)
Symmetry about initial line- Put r = 0, 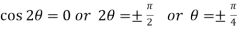
Hence the straight line 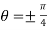 are the tangents to the curve at the pole.
are the tangents to the curve at the pole.
Values of ‘r’ as 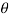 changes from 0 to π-
changes from 0 to π-
Table for the values of ‘r’-
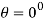 | 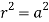 | 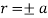 |
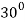 | 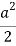 | 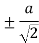 |
 | 0 | 0 |
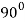 | 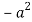 | Imaginary |
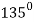 | 0 | 0 |
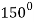 | 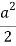 | 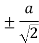 |
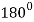 | 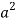 | 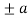 |
Here according to the table the curve does not exist for the value lying between 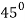 to
to 
The figure will be as follows of the curve-

Q17) Evaluate 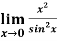 .
.
A17)
Let f(x) = 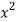 and g(x) =
and g(x) = 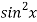 .
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
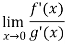
= 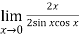
= 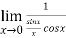
=  = 1
= 1
Q18) Evaluate 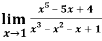
A18)
Let f(x) =  , then
, then
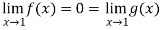
And
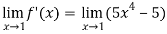 = 0
= 0
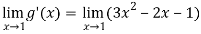 = 0
= 0
But if we use L’Hospital rule again, then we get-
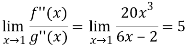
Q19) Evaluate 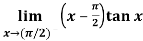
A19)
Here we find that-
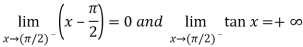
So that this limit is the form of 0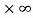 .
.
Now,
Change 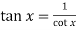 to obtain the limit-
to obtain the limit-
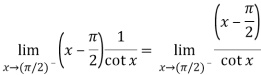
Now this is the form of 0/0,
Apply L’Hospital’s rule-
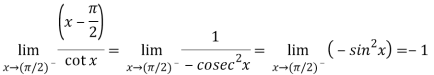
Q20) Find the maximum and minimum point of the function
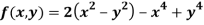
A20)
Partially differentiating given equation with respect to and x and y then equate them to zero
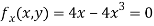
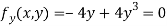
On solving above we get 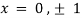
Also 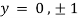
Thus we get the pair of values (0,0), (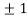 ,0) and (0,
,0) and (0,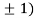
Now, we calculate
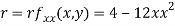
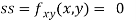

At the point (0,0)
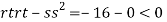
So function has saddle point at (0,0).
At the point (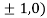
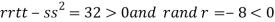
So the function has maxima at this point ( .
.
At the point (0,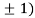

So the function has minima at this point (0,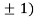 .
.
At the point (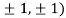
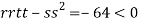
So the function has an saddle point at (