Unit - 2

Riemann integration as a limit of sum

Q1) What do you understand by anti-derivatives?

A1)

Anti-derivatives: A function F is called an anti-derivative of a function f on a given open interval if F’(x) = f(x) for all x in the interval. And the process of finding anti-derivatives is called anti-differentiation or integration. Thus, if

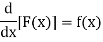
Then integrating the function f(x) produces an anti-derivative of the form F(x) + C. To emphasize this process, Equation (1) is recast using integral notation,

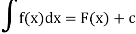
Where C is understood to represent an arbitrary constant.

Q2) What is Riemann integration as a limit of sum?

A2)

When we apply limits in indefinite integrals are called definite integrals.

If an expression is written as , here ‘b’ is called upper limit and ‘a’ is called lower limit.

If f is an increasing or decreasing function on interval [a , b], then

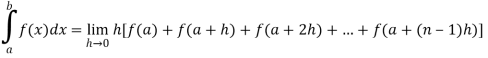
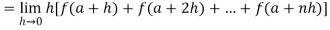
Where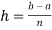 

Q3) Write down the properties of Riemann integral.

A3)

1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-

If a = b, then

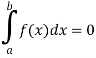
And if a>b, then

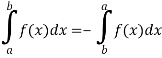
2. Integral of a constant function-

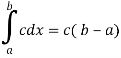
3. Constant multiple property-

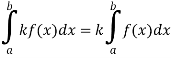
4. Interval union property-

If a < c < b, then

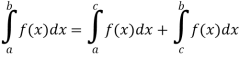
5. Inequality-

If c and d are constants such that 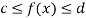for all x in [a , b], then

                          c(b – a)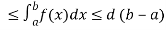

Note- if a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.

Q4) Evaluate.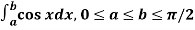

A4)

Here we notice that  f:x→cos x  is a decreasing function on [a , b],

Therefore by the definition of the definite integrals-

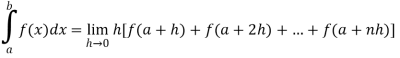
Then

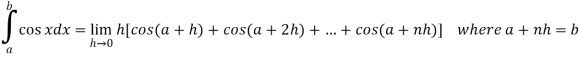
Now,

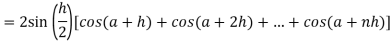
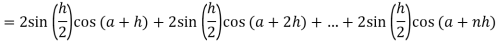
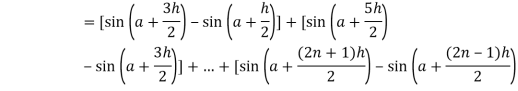
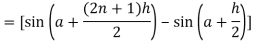
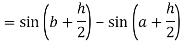
Here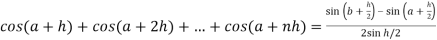

Thus

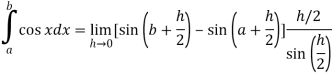
Q5) Evaluate

A5)

Here 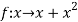is an increasing function on [1 , 2]

So that,

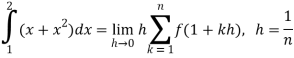
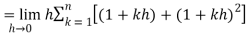
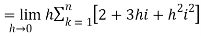
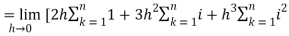  …. (1)

We know that-

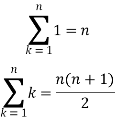
And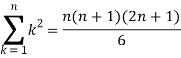
 

Then equation (1) becomes-

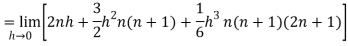
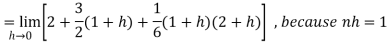
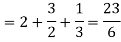
Q6) Evaluate-

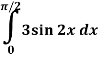A6)

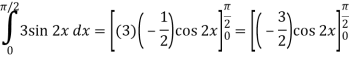
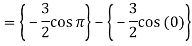
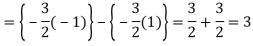
Q7) How do we integrate the function by parts?

A7)

The product rule and integral by parts:

Suppose we have two functions f(x) and g(x) then, the product rule of integration can be defined as-

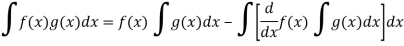
We can choose the first and second function of the integral by using “LIATE”.

L – Logarithmic

I – inverse

A- Algebraic

T- Trigonometric

E- Exponential

Q8) Integrate-

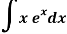
A8)

In this case the integrand is the product of the algebraic function x with the exponential function .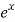

According to LIATE we should let then  we know that

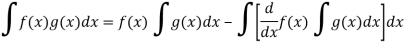
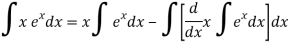
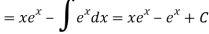
Q9) What is the reduction formula for ?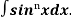

A9)

Let,                 Iⁿ = 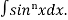  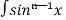  =sinxdx , if n>1

Taking 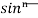 ¹x as first function and sinx as second function, integrate by parts,

                        Iⁿ = -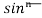¹x cosx – (n -1)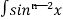cosx(-cosx)dx

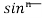                            = -¹x cosx  + (n - 1)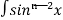cos²xdx

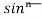                            = -¹x cosx  + (n - 1) 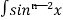( 1 - sin²x) dx

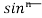                           = -¹x cosx  + (n - 1) 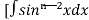- 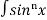dx

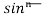=  -¹x cosx  + (n - 1) [ Iⁿ ‾ ² - Iⁿ]

By solving above

Iⁿ  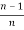= + Iⁿ‾²

This is the reduction formula for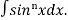

Q10) Evaluate by using reduction formula.

A10)

We know that,

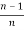+ Iⁿ‾²,     here   Iⁿ‾² =

Now using this formula,

=

                                                                      =

                                                                      =

                                                                      =

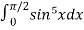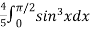
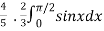
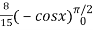
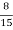
Q11) Evaluate-

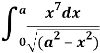
A11)

Put x = a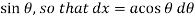

Also when x = 0,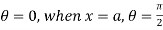

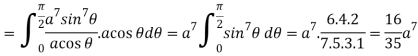
Q12) Give the reduction formula for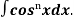

A12)

We can get the formula for

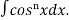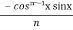= + Iⁿ‾²

We can use the following formulas to get the result easily,

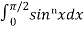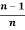= . .    ,      only if n is odd and n ≥3

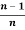   = . . . ,      only if n is even and n ≥2

We apply same formula for cos x.

Q13) Evaluate by using reduction formula.

A13)

Here, m = 4, n = 6,

                       Now we will apply above reduction formula,

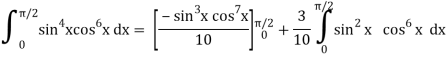
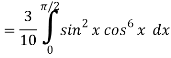
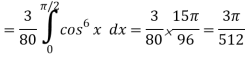
Q14) Evaluate 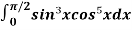by using reduction formula.

A14)

Here we can see that, m = 3 and n = 5,

                    Now we will apply reduction formula,

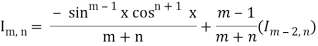
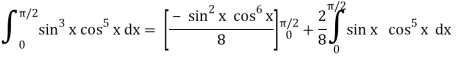
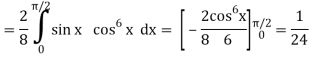
Q15) Evaluate 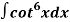by using reduction formula.

A15)

Put n = 6, 4, and 2 successively in the reduction formula for , we obtain-

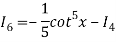
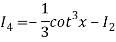
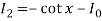
Thus

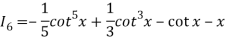
Q16) What do you understand by the partition of a closed interval?

A16)

Let us consider the closed interval [a,b] R. Then we have the following definition

Let 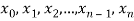, be numbers in [a,b] such that

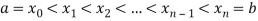
Then the ordered set P = { is called a partition of [a, b].

A partition P = {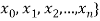 of [a, b] divides [a,b] into n closed sub-intervals

[

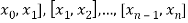
With the n + 1 partitioning points as end-points. The interval 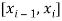 is called the ith

Sub-interval of the partition. The length of the ith sub-interval, denoted by 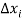is defined by

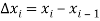
It follows that

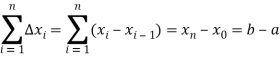
We call partition P regular if every sub-interval has the same length, that if 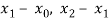,… , 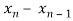are all equal.

In this case, the length of [a, b], that is b – a, is equally divided into h parts, and we get

Thus, a regular partition of [a, b] may be written as

{a, a+h, a+2h,…,a+nh} where a + nh = b: We shall denote this partition by

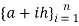
Q17) Evaluate.

A17)

Here we notice that  f:x→cos x  is a decreasing function on [a , b],

Therefore by the definition of the definite integrals-

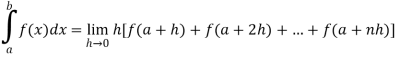
Then

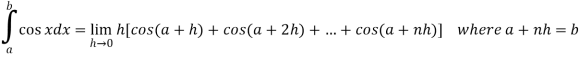
Now,

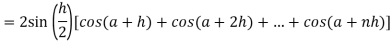
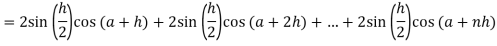
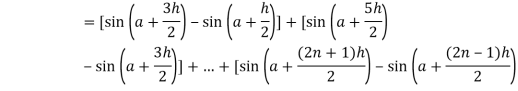
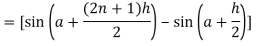
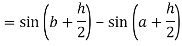
Here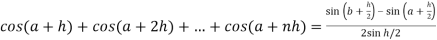

Thus

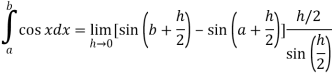
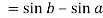
Q18) Integrate-

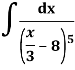
A18)

Let u =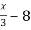

Du = 1/3 dx or dx = 3 du

Then

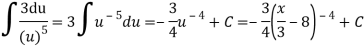
Q19) Evaluate-

A19)

Let  u =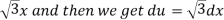

Now

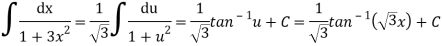
Q20) Integrate-

A20)

Let u = x – 1 so that du = dx

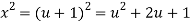
So that

= 2/7 u7/2 + 4/5 u5/2 + 2/3 u3/2 + C

= 2/7 (x – 1)7/2 + 4/5 (x -1)5/2 + 2/3 (x – 1)3/2 + C